|
Hydractinia
Jeremy Avnet and Aaron
Clauset
CS591: Complex Adaptive Systems
Prof. Stephanie Forrest
Date: May 12, 2003
DO NOT CITE - DOCUMENT HAS NOT BEEN PEER-REVIEWED
Abstract:
An agent-based simulation of the Hydractinia colonies and their
allorecognition behavior was constructed. We show evidence that
the model successfully mimics the phenomenon of colony growth,
fusing, rejection (both active and passive), morphological and
genotypic mutation, competitive exclusion and the unexpected phenomenon
of buffering. We were unable to reproduce the rock-paper-scissors
dynamic due to limitations inherent to the model.
Introduction
The Hydractinia colonial organism has been studied for its allorecognition
properties, which are thought to be a precursor for the MHC immuno-recognition
seen in mammalian immune systems. We create a model of Hydractinia
colonial growth which incorporates the three morphologies (stolon,
fused mat and unfused mat) and the genes (which
may occur in the following nine combinations on the two chromosomes:
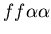 , ,
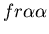 , ,
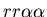 , ,
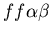 , ,
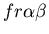 , ,
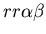 , ,
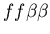 , ,
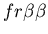 , ,
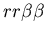 ,)
thought to be primarily responsible for the allorecognition phenomenon. ,)
thought to be primarily responsible for the allorecognition phenomenon.
Model Definition
In our conversations about how to design our Hydractinia, we
focused on several key questions:
- Agent-based or cellular automata based simulation?
- How realistic (both in terms of implementation and model realism)
is basing fight-resolution on the global property of colony
size?
- Were we to calculate colony size, how would we determine the
size of a colony after it fuses with another?
- What neighborhood (von Neumann or Moore) should be used for
a) counting nearby mat cells b) reproducing and c) fighting?
- With passive rejection (between two fused mat colonies), should
failing to allorecognize the other colony inhibit reproduction,
as it does with aggressive rejection?
- Is dying on a given round considered an 'action', i.e. if
a Hydractinia is flagged to die in a given time-step, should
it be allowed to do something else before giving up the ghost?
Agent Based Simulation
In considering the first question, we decided to employ a hybrid
model in which each cell of a square lattice is considered an agent
in a variety of states. Empty cells are flagged as dead, and may
conduct no actions. Alive cells may take one of the following
actions per turn, checked in the following order:
- Change to a dead agent with probability
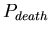 at each timestep
at each timestep
- In a random order, check each of the cells in the adjacent
nov Neumann neighborhood for successful allorecognition. The
first failure results in a fight which is immediately resolved.
- With probability
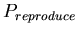 ,
spawn. If reproducing, check in a random order the von Neumann
neighborhood of adjacent cells for one that is empty. The first
empty cell found becomes the location of the new agent. ,
spawn. If reproducing, check in a random order the von Neumann
neighborhood of adjacent cells for one that is empty. The first
empty cell found becomes the location of the new agent.
- If none of the above actions were taken, do nothing.
Agent Interactions
Early in our discussions, we agreed that counting the size of a
particularly agent's larger community would be both problematic
in terms of implementation and was only loosely representative of
the real-world characteristics which this model aspect was seeking
to represent. In particular, we did not see a simple way to resolve
the difficulty of hostile colonies mutually recognizing a third
party (i.e. the genotypes
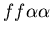 , ,
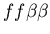 and
and
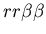 ).
Clearly in this case, the two hostile colonies should not be counted
as part of the same colony, yet from the perspective of a member
of the neutral colony, they should be. Fundamentally, the problem
with counting colony membership arises from the fact that allorecognition
is not transitive: if colony A recognizes colony B, and colony B
recognizes colony C, then colony A does not necessarily recognize
colony C. Because the idea of counting colony size is motivated
by the sharing of resources among fused colonies, it was not clear
how to resolve a situation in which colonies A shares resources
with C via B, yet A and C would not normally share resources. One
could potentially simply count all cells with which a cell would
recognize directly or indirectly (via any number of intermediaries).
However, even this approach is problematic, as one may enough up
counting all cells as being part of one super colony despite may
on-going internal conflicts! At some point, either arbitrary demarcations
must be made, or one must accept the potential that the metric does
not truly differentiate colonies in the desired way. ).
Clearly in this case, the two hostile colonies should not be counted
as part of the same colony, yet from the perspective of a member
of the neutral colony, they should be. Fundamentally, the problem
with counting colony membership arises from the fact that allorecognition
is not transitive: if colony A recognizes colony B, and colony B
recognizes colony C, then colony A does not necessarily recognize
colony C. Because the idea of counting colony size is motivated
by the sharing of resources among fused colonies, it was not clear
how to resolve a situation in which colonies A shares resources
with C via B, yet A and C would not normally share resources. One
could potentially simply count all cells with which a cell would
recognize directly or indirectly (via any number of intermediaries).
However, even this approach is problematic, as one may enough up
counting all cells as being part of one super colony despite may
on-going internal conflicts! At some point, either arbitrary demarcations
must be made, or one must accept the potential that the metric does
not truly differentiate colonies in the desired way.
As such, we decided to attempt to subsume the idea that a larger
colony has more resources to devote to fights into other aspects
of the model and have local interactions dictate all of the model
dynamics rather than a mixture of both global and local properties.
As a result, we defined a set of model probability parameters
which represented the rules given in the assignment description.
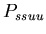 ,
the probability that a stolon-stolon or unfused-unfused fight
will be won by the aggressor ,
the probability that a stolon-stolon or unfused-unfused fight
will be won by the aggressor 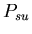 ,
the probability that a stolon-unfused mat fight will be won
by the stolon cell ,
the probability that a stolon-unfused mat fight will be won
by the stolon cell
Unfused mat cells obviously have an advantage over all other
colonies. They can fight and, due to the increased reproductive
potential that comes with nearby mat cells, reproduce faster.
Setting
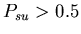 gives the stolon colonies a slight advantage, which is exacerbated
by having a larger colony size; however, this advantage should
be mitigated by an unfused mat cell colony's greater reproductive
rate. Otherwise, our model follows exactly the one described in
the assignment.
gives the stolon colonies a slight advantage, which is exacerbated
by having a larger colony size; however, this advantage should
be mitigated by an unfused mat cell colony's greater reproductive
rate. Otherwise, our model follows exactly the one described in
the assignment.
We also defined the following other paramaters for our model:
- N, the length of an edge of the square lattice on which
the agents may move
- t, the number of time steps over which the model runs
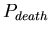 ,
the probability at each time-step that an agent will die. The
distribution of lifespans is thus a binomial one centered around ,
the probability at each time-step that an agent will die. The
distribution of lifespans is thus a binomial one centered around
![$ E[lifespan]= \frac{1}{P_{death}}$](../images/research/hydra_p2_img16.png)
-
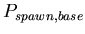 ,
the base probability of reproducing for any morphological cell
type at each time step. A binomial distribution with average ,
the base probability of reproducing for any morphological cell
type at each time step. A binomial distribution with average
![$ E[spawn,base]=\frac{1}{P_{spawn,base}}$](../images/research/hydra_p2_img18.png)
-
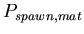 ,
the probability added to ,
the probability added to
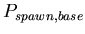 for each mat cell within Manhattan distance
for each mat cell within Manhattan distance 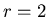 of the spawning agent.
of the spawning agent.
-
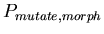 ,
the probability of choosing a random new morphology for the
daughter cells when a cell splits ,
the probability of choosing a random new morphology for the
daughter cells when a cell splits
-
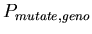 ,
the probability of choosing a random new chromosome (for each
of the two) for the daughter cells when a cell splits ,
the probability of choosing a random new chromosome (for each
of the two) for the daughter cells when a cell splits
For visualization, we used the gd libraries to write color PNG
image files of the cell-array at each timestep. Using the unix
utility convert, we collapsed the set of image files into
a MNG movie file. You can view the movies of the experiments we
cite here at http://www.theory.org/complexity/hydractinia/.
The hues red, blue and yellow were assigned
to the three morphologies, stolon, unfused mat and
fused mat respectively. Combinations of saturation and
value were used to differentiate the nine different genotypes
possible for each of the three colors.
A link to the source code for our Hydractinia model can be found
on the main
Hydractinia page.
Experiments
After much tinkering, we settled on the following values for our
model parameters:
- N: 150
- t: variable
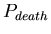 :
0.03 :
0.03 -
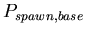 :
0.30 :
0.30
-
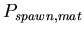 :
0.005 :
0.005
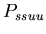 :
0.50 :
0.50 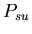 :
0.53 :
0.53 -
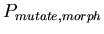 :
0.001 :
0.001
-
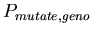 :
0.001 :
0.001
To establish that our model exhibited the required dynamics,
we performed the preliminary experiments outlined in the assignment:
- Single-cell proliferation
- Fusing colonies
- Rejecting colonies (passive and active)
To explore deeper dynamics we conducted the following experiments
(which were partially described in the assignment):
- Long-term fusing: What happens after an extremely long period
of time to two colonies which recognize each other?
- Competitive Exclusion: What kind of situation results in one
colony dominating all others in the area?
- Rock-Paper-Scissors: Is it possible to construct a rock-paper-scissors
style dynamical system using the Hydractinia colonies?
- Genotypic Mutation: What role does genotypic mutation serve
when activated? What dynamics does it lead to?
- Morphological Mutation: What role does morphological mutation
serve when activated? What dynamics does it lead to?
- What other interesting dynamics do we observe in the simulation?
Results
Preliminary Results
Our preliminary results indicated very clearly that our model was
indeed behaving as expected. Figures 1 and 2 depict the fusing of
colonies which allorecognize each other. Figure one shows a stolon
colony (red,
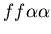 )
fusing with a fused mat colony (yellow, )
fusing with a fused mat colony (yellow, 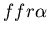 ).
Because the fused mat colony began in a corner, its reproductive
potential was somewhat hampered. Between timestep 100 and 150, the
colonies touch and successfully recognize each other. This recognition
is evidenced by the lack of dead or dying cells in the vicinity
of the intersection. This experiment was run for 5000 timesteps,
the last of which is depicted in the final image in Figure 1. Here
we can clearly see the slow diffusion of the two colonies into each
other, as shown by irregular border and the splotchiness in that
area. ).
Because the fused mat colony began in a corner, its reproductive
potential was somewhat hampered. Between timestep 100 and 150, the
colonies touch and successfully recognize each other. This recognition
is evidenced by the lack of dead or dying cells in the vicinity
of the intersection. This experiment was run for 5000 timesteps,
the last of which is depicted in the final image in Figure 1. Here
we can clearly see the slow diffusion of the two colonies into each
other, as shown by irregular border and the splotchiness in that
area.
Passive rejection is illustrated in Figure 2, in which two unfriendly
(
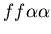 and
and
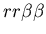 )
fused mat colonies are placed in the same vicinity. At time step
140, we can see the small region of passive rejection in which
neither reproduction as evidenced by the lack of diffusion seen
in the previous figure or fighting as evidenced by the lack of
a band of dead cells separating the two colonies. Figure 3 illustrates
hostile rejection, in which a stolon colony (red, )
fused mat colonies are placed in the same vicinity. At time step
140, we can see the small region of passive rejection in which
neither reproduction as evidenced by the lack of diffusion seen
in the previous figure or fighting as evidenced by the lack of
a band of dead cells separating the two colonies. Figure 3 illustrates
hostile rejection, in which a stolon colony (red,
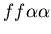 )
rejects a fused mat colony (yellow, )
rejects a fused mat colony (yellow,
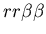 ).
Because all fights between stolon and fused mat cells result in
a dead fused mat cell, the stolon colony quickly overwhelms the
fused mat colony. ).
Because all fights between stolon and fused mat cells result in
a dead fused mat cell, the stolon colony quickly overwhelms the
fused mat colony.
An interaction between two hostile and aggressive colonies,
such as stolon or unfused mat colonies, results in a more dynamic
picture. Figure 4 illustrates such an interaction, in which a
stolon colony (red,
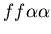 )
engages an unfused mat colony (blue, )
engages an unfused mat colony (blue,
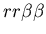 ).
The black thread which initially emerges in time step 140 and
continues throughout the experiment is evidence of the ongoing
struggle for dominance between the two colonies. Here, the balance
between the unfused mat colony's higher reproductive rate and
the stolon colony's slight advantage in a fight is seen, as this
particular dead-zone remains fairly stable between the colonies. ).
The black thread which initially emerges in time step 140 and
continues throughout the experiment is evidence of the ongoing
struggle for dominance between the two colonies. Here, the balance
between the unfused mat colony's higher reproductive rate and
the stolon colony's slight advantage in a fight is seen, as this
particular dead-zone remains fairly stable between the colonies.
Deeper Results
Having established that our model correctly mimics the behaviors
described in the assignment, we set out on the more complex experiments.
One dynamic which we found to be dominate in most heterogeneous
simulations in which the genotypes were not predefined, was that
of one colony which is neutral to both aggressors colonizing the
dead-zone between them. This phenomenon was only seen to occur between
two aggressive hostile colonies (fights between stolon and unfused
colonies), as the dead-zone is fairly stable in such fights. In
fights with fused mat colonies, the winning colony moves the dead-zone
away from the potential colonizer too quickly for it to be colonized.
However, as we can see in Figure 5, once the colonizer has moved
into the niche created by the fight, the fighting ceases as the
warring colonies have been buffered by the third party, to which
both the aggressors are neutral. This situation is exactly the kind
which we were cautious about and motivated us to forego basing cell-fights
on the size of their colony.
In some circumstances, one colony will dominate the others;
this is particularly true, if the dominating colony is able to
exclude several more vulnerable colonies, perhaps fused mat colonies
or small stolon/unfused mat colonies. In Figure 6, we see an unfused
mat colony (blue,
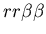 )
colony competitively exclude the other two colonies (red and yellow, )
colony competitively exclude the other two colonies (red and yellow,
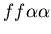 and
and
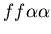 ).
The dominating colony is not inherently at an advantage over the
other two colonies, but rather is able to first destroy the defenseless
fused mat colony, and then slowly whittling away the remaining
stolon colony. The fused mat colony, in effect, prevented the
stolon colony from growing to a size large enough to hold off
the unfused mat colony. ).
The dominating colony is not inherently at an advantage over the
other two colonies, but rather is able to first destroy the defenseless
fused mat colony, and then slowly whittling away the remaining
stolon colony. The fused mat colony, in effect, prevented the
stolon colony from growing to a size large enough to hold off
the unfused mat colony.
There's no way to feasibly construct a system with a dynamical
balance such as that of the game rock-paper-scissors. This failure
is due to inherent limitations of the model, namely that fighting
is reflexive. In order to have a rock-paper-scissors situation,
all three morphologies must have both a weakness and a strength;
however, fused mat cells have no strengths, and the weakness of
unfused mat cells versus stolon cells is not substantial enough
to create the desired dynamic. As suggested in the assignment,
we tried a simulation having two colonies that fuse compete against
one rejecting colony. Figure 7 depicts the resulting dynamics.
The fusing colonies both attack the remaining colony, slowly reducing
the defending colony's numbers.
In activating genotypic mutation, we were unsure what to expect.
However, the changes in dynamics were significant. Previously,
the buffering phenomenon was the most common result between warring
colonies in a genotypically diverse environment. Generally, in
a prolonged engagement between aggressive colonies, a third party,
neutral to both, would colonize the war zone producing a buffered-peace
between the aggressive colonies. With genotypic mutation activated,
such homogeneous buffer zones were less stable. In particular,
a warring colony would generate its own buffer as a result of
a genotypic mutation which produces a viable neutral third genotype
within the dead-zone. We would frequently see such spontaneous
buffers emerge in several locations along the dead-zone, creating
a heterogeneous buffer. Further, fused mat buffers were generally
unstable, as any mutation which produced an agent hostile to the
buffer would destroy it. Figure 8 illustrates an experiment with
genotypic mutation activated that resulted in such dynamics. The
border between the stolon and unfused colonies first shows the
expected dead-zone, but it is quickly neutralized by the emergence
of small buffers of neutral cells. Figure 9 illustrates another
interesting run using the same parameters as those used in Figure
8. We can see that initially, the aggressive unfused mat and stolon
colonies create a buffer to stem their battle, while the fused
and stolon colonies fuse peacefully. However, a genotypic mutation
results in the hostile stolon subcolony shown in time step 410
eating into the fused colony. Meanwhile, the reproductive advantage
of the unfused mat colony allows it to round the tip of the stolon
colony and begin attacking the fused colony as well. Genotypic
mutation, however, saves the unfused mat colony from complete
destruction as patch of fused cells which are neutral to the aggressive
stolon subcolony persist (time step 1000).
Activating morphological mutation without also activating genotypic
mutation did not lead to an significantly different dynamics.
One might think that such additional flexibility might allow the
fused mat colonies to defend themselves slightly better (by opening
up the possibility of creating stolon or unfused mat cells), but
we did not observe this increased flexibility to prevent the fused
mat colonies from being engulfed by more aggressive colonies.
Further, once the system reached a relatively stable genotypic
steady state, the presense of morphological mutation resulted
in a morphological soup in which a colony became a diverse
mixture of the various genetically identical morphologies.
Discussion and Conclusion
Generally, we were fairly pleased with the resulting dynamics of
our model - they mimicked those described in the assignment to a
suitable degree of accuracy, and provided a few interesting and
unexpected results. In particular, the buffering phenomenon was
an unexpected (though in retrospect, understandable) action in the
given model. Even more interesting, however, was the change in the
buffering phenomenon with the activation of genotypic mutation.
Although it would be presumptuous to claim that the colonies were
knowingly doing anything, genotypic mutation provided a clear competitive
advantage to all colonies. Those which were stifled by buffering
were permitted the opportunity to penetrate the buffer via a mutation
which was friendly to the parent colony, but unfriendly to the buffer.
Further, colonies being attacked (particularly the fused mat colonies)
could survive complete destruction by local mutations which were
neutral to both the host colony and the attacking colony.
The model could be improved in many ways, however. First and
foremost, the homogeneity of a colony's structure is problematic.
In real world Hydractinia colonies are specialized morphological
structures which are omitted in our model. The transportation
and harnessing of resources was another significant omission.
In simulation after simulation, we consistently saw the fused
colonies excluded by their less passive morphological counter-parts.
Surely, in the real Hydractinia colonies, the fused mat cells
serve a more specialized role in conjunction with the other morphologies
- the benefits of mat cells promoting increased reproductive potential
were not well characterized by the model. In short, while we think
that the model did produce some very interesting dynamics, we
didn't feel like we were accurately representing the dynamics
of real Hydractinia colonies.
DO NOT CITE - DOCUMENT HAS NOT BEEN PEER-REVIEWED
Figure 1: Example of successful
allorecognition between a stolon colony (red, genotype:
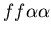 )
and fused mat colony (yellow, genotype: )
and fused mat colony (yellow, genotype:
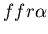 ).
Images are at timesteps 20, 70, 100, 150, 300 and 5000. In the
final snapshot, we can clearly see that the two colonies are
diffusing amongst each other to some degree, as expected with
fused colonies. ).
Images are at timesteps 20, 70, 100, 150, 300 and 5000. In the
final snapshot, we can clearly see that the two colonies are
diffusing amongst each other to some degree, as expected with
fused colonies.
|
|
Figure 2:
Example of passive rejection by two fused mat colonies (genotypes:
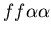 and
and
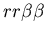 ).
Images are from timesteps 40, 90, 140, 190, 250 and 600. Not
the lack of dead cells (black) at the intersection of the two
colonies - this indicates that there is no fighting between
the colonies. ).
Images are from timesteps 40, 90, 140, 190, 250 and 600. Not
the lack of dead cells (black) at the intersection of the two
colonies - this indicates that there is no fighting between
the colonies.
|
|
Figure 3:
Example of active rejection by a stolon colony (red, genotype:
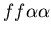 )
and a fused mat colony (yellow, genotype: )
and a fused mat colony (yellow, genotype:
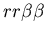 .
Images are from timesteps 50, 130, 190, 230, 350 and 600. Note
the thin region of dead cells (black) which persists at the
intersection of the two colonies; this region indicates active
rejection resulting in the death of cells (fused mat cells,
in this case). .
Images are from timesteps 50, 130, 190, 230, 350 and 600. Note
the thin region of dead cells (black) which persists at the
intersection of the two colonies; this region indicates active
rejection resulting in the death of cells (fused mat cells,
in this case).
|
|
Figure 4:
Example of active rejection between a stolon colony (red, genotype:
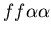 )
and an unfused mat colony (blue, genotype: )
and an unfused mat colony (blue, genotype:
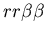 ).
The unfused mat colony grows at a higher rate than the stolon
colony as a result of the presence of other mat cells increasing
the probability of reproduction. Images are from timesteps 50,
90, 140, 200, 500 and 920. ).
The unfused mat colony grows at a higher rate than the stolon
colony as a result of the presence of other mat cells increasing
the probability of reproduction. Images are from timesteps 50,
90, 140, 200, 500 and 920.
|
|
Figure 5:
Example of the buffering phenomenon, in which the fighting region
between two hostile colonies is colonized by a third colony
which is neutral to both aggressors, resulting in a stable,
non-hostile arrangement of cells. The two hostile colonies are
unfused mat colonies (light and dark blue, genotypes:
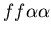 and
and
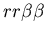 ,
while the buffering colony is a stolon (red, genotype: ,
while the buffering colony is a stolon (red, genotype:
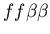 ).
Images are from timesteps 70, 150, 200, 350, 700 and 1500. ).
Images are from timesteps 70, 150, 200, 350, 700 and 1500.
|
|
Figure 6:
Example of a single colony (unfused mat, blue, genotype:
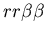 )
dominating others (stolon and fused mat, red and yellow, genotypes
( )
dominating others (stolon and fused mat, red and yellow, genotypes
(
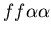 and
and
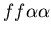 )
via competitive exclusion. The unfused mat colony, being significantly
larger, is able to slowly whittle down the resistant stolon
colony. Images are from timesteps 70, 120, 180, 300, 600 and
5000. )
via competitive exclusion. The unfused mat colony, being significantly
larger, is able to slowly whittle down the resistant stolon
colony. Images are from timesteps 70, 120, 180, 300, 600 and
5000.
|
|
Figure 7:
Rock-Paper-Scissors experiment (as suggested in the assignment),
in which two colonies fuse (unfused mat and stolon, blue and
red, genotypes:
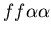 and
and
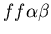 ),
while one rejects (stolon, red, genotype: ),
while one rejects (stolon, red, genotype:
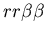 ). ).
|
|
Figure 8:
Activating genotypic mutation for the system used in Figure
6 (example 1). Images are timesteps 50, 140, 250, 380, 450 and
800.
|
|
Figure 9:
Activating genotypic mutation for the system used in Figure
6 (example 2). Images are timesteps 110, 320, 410, 500, 640
and 1000.
|
|
DO NOT CITE - DOCUMENT HAS NOT BEEN PEER-REVIEWED
|
|

