a)
| b)
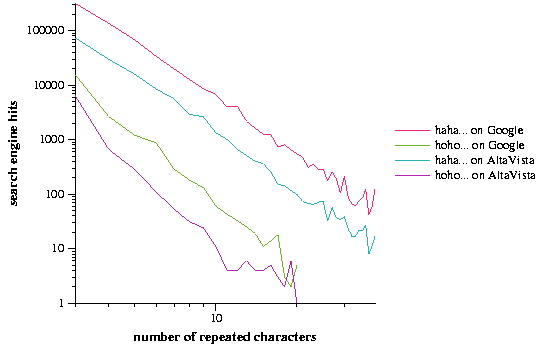
|
This work was released as UNM Computer Science Department Tech Report TR-CS-2001-23. These reports are archived at: http://www.cs.unm.edu/tech_reports/.
|
Computer Science Department University of New Mexico Albuquerque, NM 87131 USA dlchao@cs.unm.edu
| Department of Genetics and Lipper Center for Computational Genetics Harvard Medical School Boston, MA 02115 USA patrik@genetics.med.harvard.edu |
If one uses a commercial internet search engine to search for increasingly long versions of variable-length interjectives on the web (e.g. ``whee'', ``wheee'', ``wheeee'', etc.), the number of pages found containing these longer words falls off as a power law. The exponents for the length frequency distributions of different interjectives are not the same, although they may cluster around a few exponents. Surprisingly, the exponents are much larger than the -1 predicted by Zipf's Law. We believe that the restricted domain of variable-length phatic interjectives is an interesting subset of English that can provide an alternative simple model system of word length distributions.
The variability in the written length of phatic interjectives (e.g. ``whee'', ``wheeee'', ``aah'', ``aaah'') is of great interest to linguists and computer scientists. 1In this paper, we examine the distribution of variable-length phatic interjectives on the largest corpus of such words ever assembled: the World Wide Web. By using commercial internet search engines, we can quickly get a rough estimate of the distribution of these words on the internet.
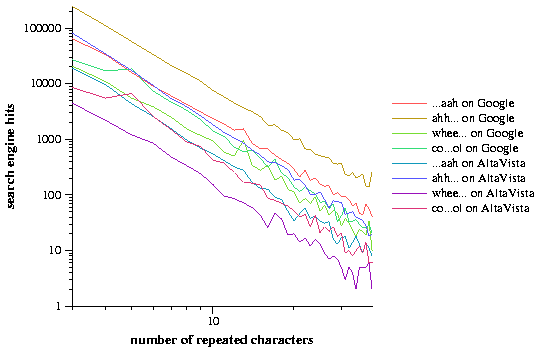
The web search engines Google [4] and AltaVista [1] were used to estimate the number of occurrences of length variations on the interjectives ``aah'', ``ahh'', ``cool'', ``ooh'', and ``whee'' on the World Wide Web. Ideally, the search engines return the number of web pages that contain a particular word, while in reality a single search engine probably covers less than 20% of the web [5]. Two different search engines were employed in order to verify the consistency of their results and to increase the search coverage. These words all feature a single letter that can be repeated to create longer versions of the words, for example, ``ahh'' can become ``ahhhhhhh''. These particular words were chosen because their extended versions can be found at relatively high frequencies on the Web. The authors recorded the number of hits returned by the search engines for these words and varied the number of repeated letters in them, from three to thirty-nine (e.g. from ``wheee'' to ``wheeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee''). Variations with only one or two repetitions, such as ``whe'' and ``whee,'' were not considered due to the appearance of ``whe'' in non-interjectives such as ``whet'' and ``wheel.'' ``Wheee'' is a reasonable starting point as it does not begin any words in the standard English lexicon. We also investigated the frequencies of interjectives with two-letter repeated elements: ``haha'' and ``hoho,'' repeating the two-letter units three to thirty-nine times. The data for ``hoho'' was truncated after 20 repeated units because the longer words had frequencies close to zero. The results are summarized in Table 1.
The frequency distributions of the lengths of these phatic interjectives exhibit clear power-law relationships (Figure 1). With the exception of the words based on ``ooh'', the interjectives with a single repeating letter (i.e. ``aah'', ``ahh'', ``cool'', and ``whee'') have slopes of approximately -3.0, which we call We. The slopes of interjectives that have two-letter repeating units (i.e. ``haha'' and ``hoho'') is higher, from -3.42 to -4.30.
We had expected the frequency distributions of the lengths of phatic interjectives to obey Zipf's law [8], which observes (but does not explain) that the ranked frequencies of words in a corpus follow a power law with an exponent of -1. However, we found much higher exponents, ranging from -2.86 to -4.30. Therefore, we do not believe that the published explanations of Zipf's law (such as [6]) explain the distribution of variable-length interjectives on the Web. We believe that this group of words comprises a simple model system for studying word lengths that provides an alternative to ``monkey languages'' [3], in which text is simply a random stream of letters and spaces like the proverbial monkey banging on a typewriter.
The frequency of the variations of words on the World Wide Web depend on at least two factors: the frequencies with which authors of web content use these variations and the frequencies at which this content is duplicated and reached by search engines.
We believe that the first distribution is either exponential or follows a power law. If each typist of interjectives follows a Poisson process in which after each character the typist has constant probability of quitting, the distribution of lengths would be exponential. If, instead of typing each character of the word individually, the typist doubles the number at each step by copying and pasting the block of all repeated letters at each step, then the word lengths would have a power law distribution.
The duplication of content may induce a power law, dominating the original underlying distribution produced by the web authors. We assume there is a distribution of pages that favors shorter phatic interjectives. An important source of web content duplication is the quoting of messages, especially e-mail, in replies. Replies to messages also get replies, and the original message is often still present in these chains of replies for many ``generations.'' This would contribute to bits of text that are replicated an exponential number of times. As in Barabási's model of the formation of scale-free networks [2], the positive feedback loop of often-quoted messages getting quoted even more often can cause a power law distribution. As more mail and other such messages are archived on the World Wide Web, these effects will gain importance.
There are a large number of similar experiments that can be performed to obtain a more accurate characterization of interjective length frequencies on the World Wide Web. These searches should be tried on different search engines. Google relies heavily on crawling the web from its current database, which may form a scale-free network a priori. Studying the number of letters that people actually use in long phatic interjectives would also contribute to our understanding of this phenomenon. This data may be difficult to acquire because standard corpuses consisting of published works typically do not have long interjectives. 2Variable-length interjectives are a small subset of the distribution of words than is usually studied, yet yield interesting behavior and should prove easier to investigate. Further research in unbounded phatic interjectives will give insight into the mechanisms behind Zipf's Law, the nature of the web, and the patience of authors.
a)

| b)
|
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.48)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 w.tex
The translation was initiated by Dennis Chao on 2001-09-04
and was hand-edited.