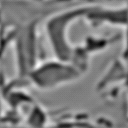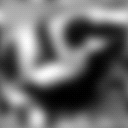UNM Scheme: Digital Image Processing Library

• (make-image <number m> <number n> . <function>) Given a positive integer <number m>, a positive integer <number n>, and a <function> returning a real (or complex) number, make-image returns a real (or complex) image with m rows and n columns. The value of the result image at location (i, j) is computed by applying <function> to i and j. If <function> is not specified, the result image will be initialized to zero everywhere. For example, > (make-image 32 32) #<image: rows = 32 cols = 32> >

  

  > (make-image 128 128 (lambda (i j) (+ i j))) #<image: rows = 128 cols = 128> >

  

  > (define harmonic-signal (lambda (u v) (lambda (m n) (exp (* -6.28319i (+ (* u m) (* v n))))))) > > (define signal (make-image 128 128 (harmonic-signal (/ 3 128) (/ 2 128)))) > signal #<complex-image: rows = 128 cols = 128> >

  

• (read-image <string filename>) Given <string filename>, the name of a file containing an image stored in ASCII .pgm format, read-image reads the file and returns the image. For example, > (define frog (read-image "frog.pgm")) > frog #<image: rows = 225 cols = 242>

  

• (write-image <image> <string filename>) Given a positive integer <image> and <string filename>, write-image creates a file representing the image in ASCII .pgm format. Due to limitations of the ASCII .pgm format, only positive integer images can be read by read-image or written by write-image. For example, > (write-image frog "frog.pgm") creates a file which looks like this: P2 # Creator: University of New Mexico Scheme 2.0 242 225 255 151 151 151 151 151 150 150 149 148 147 146 145 145 142 142 143 145 148 152 156 158 159 159 159 159 157 155 152 150 153 152 151 149 149 149 149 150 149 149 149 149 149 149 149 149 149 146 144 141 138 136 133 132 136 136 136 136 136 136 136 136 139 138 138 138 137 136 136 136 135 135 136 136 137 137 138 138 138 137 138 137 138 137 138 137 135 134 134 134 138 141 147 150 149 147 143 138 134 132 131 130 129 129 130 132 134 136 137 137 137 137 138 139 142 145 147 149 145 146 150 153 156 159 161 163 156 158 161 163 167 170 174 175 181 183 . . .

• (image? <sexpr>) Returns #t if <sexpr> is an image and #f otherwise. For example, > (image? frog) #t >
• (image-ref <image> <number i> <number j>) Given a real (or complex) <image>, a real positive <number i>, and a real positive <number j>, image-ref returns the value at location (i, j). If i is less than zero or greater than the number of rows of <image> or j is less than zero or greater than the number of columns of <image>, then a value of zero is returned. If either i or j is not an integer, then the return value is computed by bilinear interpolation. For example, > (image-ref frog 100 100) 56 >
• (image-set! <image> <number i> <number j> <number x>) Given a real (or complex) <image>, a positive integer <number i>, a positive integer <number j>, and a real (or complex) <number value>, image-set! sets the value of the image at location (i, j) to x. It is an error if i is less than zero or greater than the number of rows of <image> or if j is less than zero or greater than the number of columns of <image>. For example, > (define foo (make-image 32 32)) > (image-set! foo 16 16 255) > foo #<image: rows = 32 cols = 32> >

  

• (image-rows <image>) Returns the number of rows of <image>. For example, > (image-rows frog) 225 >
• (image-cols <image>) Returns the number of columns of <image>. For example, > (image-cols frog) 242 >
• (image-transpose <image>) Returns an image created by interchanging the rows and columns of real (or complex) <image>, i.e., the value at location (i, j) of the result image is the value of <image> at location (j, i). For example, > (image-transpose frog) #<image: rows = 242 cols = 225> >

  

• (convolve-rows <image> <vector>) Given a real (or complex) <image> and a <vector> consisting solely of real (or complex) numbers representing a 1D convolution kernel, convolve-rows returns the 1D discrete periodic convolution of the rows of the image with the kernel. For example, > (convolve-rows frog #(1 -1)) #<image: rows = 225 cols = 242> >

• (convolve-cols <image> <vector>) Given a real (or complex) <image> and a <vector> consisting solely of real (or complex) numbers representing a 1D convolution kernel, convolve-cols returns the 1D discrete periodic convolution of the columns of the image with the kernel. For example, > (convolve-cols frog #(1 -1)) #<image: rows = 225 cols = 242> >
  > (let ((dx (convolve-rows frog #(1 -1))) (dy (convolve-cols frog #(1 -1)))) (sqrt (+ (* dx dx) (* dy dy)))) #<image: rows = 225 cols = 242> >

  

• (convolve <image> <array>) Given a real (or complex) <image> and an <array> consisting solely of real (or complex) numbers representing a 2D convolution kernel, convolve returns the 2D discrete periodic convolution of the image with the kernel. For example, > (convolve frog #(#(1 1 1) #(1 -8 1) #(1 1 1))) #<image: rows = 225 cols = 242> >

• (downsample-cols <image>) Given a real (or complex) <image>, downsample-cols returns the image created by discarding the odd numbered rows, i.e., the value at location (i, j) of the result image is the value of <image> at location (2i, j). For example, > (downsample-cols frog) #<image: rows = 113 cols = 242> >

• (downsample-rows <image>) Given a real (or complex) <image>, downsample-rows returns the image created by discarding the odd numbered columns, i.e., the value at location (i, j) is the value of <image> at location (i, 2j). For example, > (downsample-rows frog) #<image: rows = 225 cols = 121> >

• (downsample <image>) > (define tiny-frog (downsample frog)) > tiny-frog #<image: rows = 113 cols = 121> >

• (upsample-cols <image>) Given a real (or complex) <image>, upsample-cols returns an image with twice the number of rows where the value at location (i, j) of the result image is the value of <image> at location (i/2, j) if i is even and zero otherwise. For example, > (upsample-cols tiny-frog) #<image: rows = 226 cols = 121> >

  

• (upsample-rows <image>) Given a real (or complex) <image>, upsample-rows returns an image with twice the number of columns where the value at location (i, j) of the result image is the value of <image> at location (i, j/2) if j is even and zero otherwise. For example, > (upsample-rows tiny-frog) #<image: rows = 113 cols = 242> >

• (upsample <image>) Given a real (or complex) <image>, upsample returns an image with twice the number of rows and columns where the value at location (i, j) of the result image is the value of <image> at location (i/2, j/2) if both i and j are even and zero otherwise. For example, > (upsample tiny-frog) #<image: rows = 226 cols = 242> >

  

• (image-pad <image> <number m> <number n>) Given a real (or complex) <image>, positive integer <number m>, and positive integer <number n>, image-pad returns a real (or complex) image with m rows and n columns where the value at location (i, j) of the result image is the value of <image> at location (i, j) if i is less than m and j is less than n and zero otherwise. For example, > (image-pad tiny-frog 200 200) #<image: rows = 200 cols = 200> >

  

• (image-crop <image> <number i0>,<number j0> <number m> <number n>)

  Given a real (or complex) <image>, positive integer <number i₀>, positive integer <number j₀>, positive integer <number m>, and positive integer <number n>, image-crop returns a real (or complex) image with m rows and n columns where the value at location (i, j) of the result image is the value of <image> at location (i₀ + i, j₀ + j). For example, > (define frog-part (image-crop frog 64 64 128 128)) > frog-part #<image: rows = 128 cols = 128> >

  

• (left-to-right <image X1> ... <image Xn>)

  Given n real (or complex) images, <image X₁> ... <image X_n>, all with the same number of rows, left-to-right returns a real (or complex) image formed by concatenating the images from left to right. For example, > (left-to-right tiny-frog tiny-frog) #<image: rows = 225 cols = 484> >

• (top-to-bottom <image X1> ... <image Xn>)

  Given n real (or complex) images, <image X₁> ... <image X_n>, all with the same number of columns, top-to-bottom returns a real (or complex) image formed by concatenating the images from top to bottom. For example, > (top-to-bottom tiny-frog tiny-frog) #<image: rows = 450 cols = 242> >

  

• (make-filter <number m> <number n> . <function>) Given a positive integer <number m>, a positive integer <number n>, and a <function> returning a real (or complex) number, make-filter returns a real (or complex) image with m rows and n columns. Let x equal i if i is less than m/2 and i - m otherwise and let y equal j if j is less than n/2 and j - n otherwise. To match the periodicity of the 2D discrete Fourier spectrum, the value of the result image at location (i, j) is computed by applying <function> to x and y, e.g., the value at location (0, 0) is the result of applying <function> to 0 and 0, the value at (m-1, n-1) is the result of applying <function> to -1 and -1. If <function> is not specified, the result image will be initialized to zero everywhere. For example, > (make-filter 128 128 (lambda (i j) (+ i j))) #<image: rows = 128 cols = 128> >

  

  > (define laplacian-of-gaussian (lambda (stddev) (lambda (i j) (let* ((r (+ (* i i) (* j j))) (x (/ r 2.0 stddev))) (* (/ -3.14159 stddev stddev) (- 1.0 x) (exp (- x))))))) > > (define d2g (make-filter 128 128 (laplacian-of-gaussian 8.0))) > d2g #<image: rows = 128 cols = 128> >

• (fft <image>) Given a real (or complex) <image>, fft returns a complex image representing its 2D discrete Fourier transform (DFT). Because the DFT is computed using the Fast Fourier Transform (FFT) algorithm, the number of rows and columns of <image> must both be powers of two, i.e., 2^K where K is an integer. For example, > (log (magnitude (fft frog-part))) #<image: rows = 128 cols = 128> >

  

  > (fft d2g) #<complex-image: rows = 128 cols = 128> > > (define gaussian (lambda (variance) (lambda (i j) (let* ((r (+ (* i i) (* j j))) (x (/ r 6.28319 variance))) (exp (- x)))))) > > (define g (make-filter 128 128 (gaussian 8.0))) > g #<image: rows = 128 cols = 128> > > (fft g) #<complex-image: rows = 128 cols = 128> >

• (ifft <image>) Given a real (or complex) <image>, fft returns a complex image representing its 2D inverse discrete Fourier transform (DFT). Because the inverse DFT is computed using the Fast Fourier Transform (FFT) algorithm, the number of rows and columns of <image> must both be powers of two, i.e., 2^K where K is an integer. For example, > (ifft (* (fft frog-part) (fft d2g))) #<complex-image: rows = 128 cols = 128> >
  > (ifft (* (fft frog-part) (fft g))) #<complex-image: rows = 128 cols = 128> >

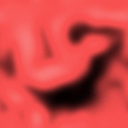
• (real-part <complex z | complex-image Z>) Given <complex z> (or <complex-image Z>), real-part returns a real number (or image) representing the real part of z (or Z). For example, > (define cosine (real-part signal)) > cosine #<image: rows = 128 cols = 128> >
  > (real-part (ifft (* (fft frog-part) (fft d2g)))) #<image: rows = 128 cols = 128> >
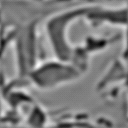
  > (real-part (ifft (* (fft frog-part) (fft g)))) #<image: rows = 128 cols = 128> >

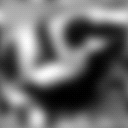
• (imag-part <complex z | complex-image Z>) Given <complex z> (or <complex-image Z>), real-part returns a real number (or image) representing the imaginary part of z (or Z). For example, > (define sine (imag-part signal)) > sine #<image: rows = 128 cols = 128> >

• (complex <number x | image X> <number y | image Y>) Given real <number x> (or real <image X>) and real <number y> (or real <image Y>) complex returns a complex number (or image) with real part x (or X) and imaginary part y (or Y). For example, > (complex cosine sine) #<complex-image: rows = 128 cols = 128> >

• (complex-image->rectangular <complex-image>) Given <complex-image>, complex-image->rectangular returns a list containing two real images representing its real and imaginary parts. For example, > (apply left-to-right (complex-image->rectangular signal)) #<image: rows = 128 cols = 256> >

• (magnitude <complex z | complex-image Z>) Given <complex z> (or <complex-image Z>), magnitude returns a real number (or image) representing the magnitude of z (or Z). For example, > (magnitude signal) #<image: rows = 128 cols = 128> >

• (angle <complex z | complex-image Z>) Given <complex z> (or <complex-image Z>), angle returns a real number (or image) representing the phase of z (or Z). For example, > (angle signal) #<image: rows = 128 cols = 128> >

• (complex-image->polar <complex-image>) Given <complex-image>, complex-image->polar returns a list containing two real images representing its magnitude and phase. For example, > (apply left-to-right (complex-image->polar signal)) #<image: rows = 128 cols = 256> >

• (+ <number x1 | image X1> ... <number xn | image Xn>)

  Returns the sum of its n arguments, each of which is a real (or complex) number (or image), i.e., <number x₁ | image X₁> ... <number x_n | image X_n>. If all of its arguments are numbers, then the sum of the numbers is returned. If any of its arguments are images, and all of the images have the same numbers of rows and columns, then a real (or complex) image with the same dimensions is returned. If all of its arguments are images, then the value of the result image at location (i, j) is the sum of the n values of the n images at location (i, j). If some of its arguments are images and some are numbers then the numbers are (in effect) promoted to images with the same numbers of rows and columns as the image arguments. 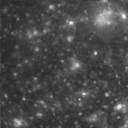For example, > (define callisto (read-image "callisto.pgm")) > callisto #<image: rows = 128 cols = 128> >

  

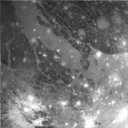
  > (define ganymede (read-image "ganymede.pgm")) > ganymede #<image: rows = 128 cols = 128> >

  

  > (+ callisto ganymede) #<image: rows = 128 cols = 128> >

  

• (- <number x1 | image X1> ... <number xn | image Xn>)

  Returns the difference of its first argument and the sum of the remaining n-1 arguments, each of which is a real (or complex) number (or image), i.e., <number x₁ | image X₁> ... <number x_n | image X_n>. If all of its arguments are numbers, then the difference of the first number and the sum of the remaining numbers is returned. If any of its arguments are images, and all of the images have the same numbers of rows and columns, then a real (or complex) image with the same dimensions is returned. If all of its arguments are images, then the value of the result image at location (i, j) is the difference of the value of the first image at location (i, j) and the sum of the n-1 values of the remaining n-1 images at location (i, j). If some of its arguments are images and some are numbers then the numbers are (in effect) promoted to images with the same numbers of rows and columns as the image arguments. For example, > (- callisto ganymede) #<image: rows = 128 cols = 128> >

  

• (* <number x1 | image X1> ... <number xn | image Xn>)

  Returns the product of its n arguments, each of which is a real (or complex) number (or image), i.e., <number x₁ | image X₁> ... <number x_n | image X_n>. If all of its arguments are numbers, then the product of the numbers is returned. If any of its arguments are images, and all of the images have the same numbers of rows and columns, then a real (or complex) image with the same dimensions is returned. If all of its arguments are images, then the value of the result image at location (i, j) is the product of the n values of the n images at location (i, j). If some of its arguments are images and some are numbers then the numbers are (in effect) promoted to images with the same numbers of rows and columns as the image arguments. 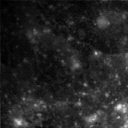For example, > (* callisto ganymede) #<image: rows = 128 cols = 128> >

  

• (/ <number x1 | image X1> ... <number xn | image Xn>)

  Returns the quotient of its first argument and the product of its remaining n-1 arguments, each of which is a real (or complex) number (or image), i.e., <number x₁ | image X₁> ... <number x_n | image X_n>. If all of its arguments are numbers, then the quotient of the first number and the product of the remaining numbers is returned. If any of its arguments are images, and all of the images have the same numbers of rows and columns, then a real (or complex) image with the same dimensions is returned. If all of its arguments are images, then the value of the result image at location (i, j) is the quotient of the value of the first image at location (i, j) and the product of the n-1 values of the remaining n-1 images at location (i, j). If some of its arguments are images and some are numbers then the numbers are (in effect) promoted to images with the same numbers of rows and columns as the image arguments. For example, > (/ callisto ganymede) #<image: rows = 128 cols = 128> >

  

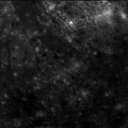
• (array->image <array>) Given an <array> consisting entirely of real (or complex) numbers, array->image returns a real (or complex) image with the same dimensions as the array. For example, > (set-image-display-scale! 40.0) > (array->image #(#(1 2 3) #(4 5 6) #(7 8 9))) #<image: rows = 3 cols = 3> >

  

• (image->array <image>) Given a real (or complex) <image>, image->array returns an array with the same dimensions as the image. For example, > (image->array (array->image #(#(1 2 3) #(4 5 6) #(7 8 9)))) #(#(1 2 3) #(4 5 6) #(7 8 9)) >

• (> <number x1 | image X1> ... <number xn | image Xn>)

  Returns #t if its n real number arguments, <number x₁> ... <number x_n>, form a strictly decreasing sequence and #f otherwise. If any of its arguments are real images, and all of the images have the same numbers of rows and columns, then a binary image with the same dimensions is returned. If all of its arguments are real images, <image X₁> ... <image X_n>, then the value of the result image at location (i, j) is one if the n values of the n real images at location (i, j) form a strictly decreasing sequence and zero otherwise. If some of its arguments are real images and some are real numbers then the numbers are (in effect) promoted to real images with the same numbers of rows and columns as the image arguments. For example, > (define stop (read-color-image "stop.ppm")) #<color-image: rows = 86 cols = 159> >

  

  > (define binary-stop (> (apply + (color-image->rgb stop)) 400)) #<image: rows = 86 cols = 159> >

• (< <number x1 | image X1> ... <number xn | image Xn>)

  Returns #t if its n real number arguments, <number x₁> ... <number x_n>, form a strictly increasing sequence and #f otherwise. If any of its arguments are real images, and all of the images have the same numbers of rows and columns, then a binary image with the same dimensions is returned. If all of its arguments are real images, <image X₁> ... <image X_n>, then the value of the result image at location (i, j) is one if the n values of the n real images at location (i, j) form a strictly increasing sequence and zero otherwise. If some of its arguments are real images and some are real numbers then the numbers are (in effect) promoted to real images with the same numbers of rows and columns as the image arguments. For example, > (define noise (< (make-image 86 159 (lambda (i j) (random 100))) 1)) > noise #<image: rows = 86 cols = 159> >

  

• (= <number x1 | image X1> ... <number xn | image Xn>)

  Returns #t if its n real (or complex) number arguments, <number x₁> ... <number x_n>, are equal and #f otherwise. If any of its arguments are images, and all of the images have the same numbers of rows and columns, then a binary image with the same dimensions is returned. If all of its arguments are images, <image X₁> ... <image X_n>, then the value of the result image at location (i, j) is one if the n values of the n images at location (i, j) are equal and zero otherwise. If some of its arguments are images and some are numbers then the numbers are (in effect) promoted to images with the same numbers of rows and columns as the image arguments. For example, > (define noisy-stop (= (+ binary-stop noise) 1)) > noisy-stop #<image: rows = 86 cols = 159> >

  

• (set-image-display-scale! <number>) Given a real positive <number>, set-image-display-scale! sets the system parameter which determines the physical size of displayed images (the default value of this parameter is one).

• (image-normalize <image>) Given a real <image>, image-normalize returns a real image with the same dimensions where the values have been normalized to lie in the interval [0, 1].

• (image-shrink <image> <number x>) Given a real (or complex) <image> and a real positive <number x>, image-shrink returns a real (or complex) image with the same dimensions. Let z be the value of <image> at location (i, j). If |z| < x, then the value of the result image at location (i, j) is zero. Otherwise, it is z - x if z > 0 and z + x if z < 0. If <image> is complex, then the value of the complex result image at location (i, j) is zero if |z| < x, otherwise the result has the same phase as z but the amplitude is decreased by x.

• (median-filter <image> <number m> <number n>) Given a real <image>, and two positive integers, <number m> and <number n>, median-filter returns a real image with the same dimensions where each pixel (i, j) in <image> is replaced by the pixel with median value in the neighborhood of size <number m> times <number n> centered on (i, j).
  > (define median-filtered-frog (median-filter frog 5 5)) > median-filtered-frog #<image: rows = 225 cols = 242> >

  

• (fold <function> <image>) Given a <function> of two <sexpr>'s which returns a <sexpr>, fold returns the <sexpr> which results from repeatedly applying <function> to: 1) the result accumulated to this point (initially the value of the first pixel); and 2) the value of the next pixel. Note: The order is unspecified.

• (matrix-product <image X1> <image X2>)

  Given real (or complex) <image X₁> and real (or complex) <image X₂>, where the number of columns of X₁ equals the number of rows of X₂, matrix-product returns an image representing the matrix product of X₁ and X₂. > (matrix-product frog-part frog-part) #<image: rows = 128 cols = 128> >

  

• (image-map <function> <image X1> ... <image Xn>)

  Given a <function> of n real (or complex) numbers which returns a real (or complex) number, and n real (or complex) images, <image X₁> ... <image X_n> all with the same number of rows and columns, image-map returns a real (or complex) image with the same dimensions. The value of the result image at location (i, j) is computed by applying <function> to the n values of the n images at location (i, j). Note: Although image-map will work with any function of n real (or complex) numbers which returns a real (or complex) number, it is generally only necessary to use image-map when the definition of <function> includes special forms. For example, > (image-map (lambda (p) (if (> p 0) (* -1 p (log2 p)) 0)) frog) #<image: rows = 225 cols = 242> >

  

• (read-color-image <string filename>) Given <string filename>, the name of a file containing an image stored in ASCII .ppm format, read-color-image reads the file and returns the color image. For example, > (define cacti (read-color-image "cacti.ppm")) > cacti #<color-image: rows = 195 cols = 200> >

  

• (write-color-image <color-image> <string filename>) Given a positive integer <color-image> and <string filename>, write-color-image creates a file representing the color image in ASCII .ppm format. Due to limitations of the ASCII .ppm format, only positive integer color images can be read by read-color-image or written by write-color-image. For example, > (write-color-image cacti "cacti.ppm") > creates a file which looks like this: P3 # Creator: University of New Mexico Scheme 2.0 200 195 254 83 89 94 85 94 102 100 112 126 121 130 148 110 120 141 102 114 136 104 116 131 134 138 151 143 140 153 98 106 119 92 106 122 120 124 137 125 121 124 129 126 132 120 124 132 122 121 128 124 114 115 93 92 96 70 78 90 90 97 108 113 118 129 124 130 139 118 126 141 115 127 146 133 140 154 119 122 129 111 110 104 108 116 111 107 120 128 109 115 121 115 118 125 99 111 109 94 108 95 89 109 106 90 110 118 83 101 111 81 100 112 96 117 129 97 119 127 97 116 126 97 114 122 72 92 90 74 99 104 91 119 140 84 112 120 . . .
• (color-image? <sexpr>) Returns #t if <sexpr> is a color image and #f otherwise. For example, > (color-image? cacti) #t >
• (color-image-red <color-image>) Given <color-image>, color-image-red returns a real image representing its red color component. For example, > (define red (color-image-red cacti)) > red #<image: rows = 195 cols = 200> >

  

• (color-image-green <color-image>) Given <color-image>, color-image-green returns a real image representing its green color component. For example, > (define green (color-image-green cacti)) > green #<image: rows = 195 cols = 200> >

  

• (color-image-blue <color-image>) Given <color-image>, color-image-blue returns a real image representing its blue color component. For example, > (define blue (color-image-blue cacti)) #<image: rows = 195 cols = 200> >

  

• (rgb->color-image <image R> <image G> <image B>) Given real <image R>, real <image G>, and real <image B>, rgb->color-image returns a color image with red color component, R, green color component, G, and blue color component, B. > (rgb->color-image red green blue) #<color-image: rows = 195 cols = 200> >

  

• (color-image->rgb <color-image>) Given <color-image>, color-image->rgb returns a list containing three real images representing the red, green, and blue color components of <color-image>. For example, > (apply left-to-right (color-image->rgb cacti)) #<image: rows = 195 cols = 600> >

  

• (rgb->hsi <image R> <image G> <image B>) Given real <image R>, real <image G>, and real <image B>, representing the red, green, and blue color components of a color image, rgb->hsi returns a list containing three real images representing the hue, saturation, and intensity of the color image. For example, > (define hsi (rgb->hsi red green blue)) > hsi (#<image: rows = 195 cols = 200> #<image: rows = 195 cols = 200> #<image: rows = 195 cols = 200>) > (define hue (car hsi)) > hue #<image: rows = 195 cols = 200> >

  

  > (define saturation (cadr hsi)) > saturation #<image: rows = 195 cols = 200> >

  

  > (define intensity (caddr hsi)) > intensity #<image: rows = 195 cols = 200> >

  

• (hsi->rgb <image H> <image S> <image I>) Given real <image H>, real <image S>, and real <image I>, representing the hue, saturation, and intensity of a color image, hsi->rgb returns a list containing three real images representing the red, green, and blue color components of the color image. For example, > (hsi->rgb hue saturation intensity) (#<image: rows = 195 cols = 200> #<image: rows = 195 cols = 200> #<image: rows = 195 cols = 200>) >

• (color-image->hsi <color-image>) Given <color-image>, color-image->hsi returns a list containing three real images representing the hue, saturation, and intensity of <color-image>. For example, > (color-image->hsi cacti) (#<image: rows = 195 cols = 200> #<image: rows = 195 cols = 200> #<image: rows = 195 cols = 200>) >

• (hsi->color-image <image H> <image S> <image I>) Given real <image H>, real <image S>, and real <image I>, representing the hue, saturation, and intensity of a color image, hsi->color-image returns the color image. For example, > (hsi->color-image hue saturation intensity) #<color-image: rows = 195 cols = 200> >

  

• (make-hot-image <image>) Given a real <image>, make-hot-image returns a color image with the same dimensions. The R, G, B values of the result image at (i, j) are determined by using the value of <image> at (i, j) to index three lookup tables. These lookup tables implement a false coloring scheme which maps small values to black, large values to white, and intermediate values to shades of red, orange, and yellow (in that order). > (make-hot-image frog) #<color-image: rows = 225 cols = 242> >

  

• (dilate <image> . <array>) Given a binary <image>, and an <array> consisting solely of zeros and ones representing a structuring element, dilate returns the morphological dilation of <image> with the structuring element. The default value of <array> is #(#(1 1) #(1 1)). For example, > (dilate binary-stop #(#(0 0 1 0 0) #(0 1 1 1 0) #(1 1 1 1 1) #(0 1 1 1 0) #(0 0 1 0 0))) #<image: rows = 86 cols = 159> >

  

• (erode <image> . <array>) Given a binary <image>, and an <array> consisting solely of zeros and ones representing a structuring element, erode returns the morphological erosion of <image> with the structuring element. The default value of <array> is #(#(1 1) #(1 1)). For example, > (erode binary-stop #(#(0 0 1 0 0) #(0 1 1 1 0) #(1 1 1 1 1) #(0 1 1 1 0) #(0 0 1 0 0)))) #<image: rows = 86 cols = 159> >

  

• (outline <image> . <number x> <number y>)

  Given <image>, a real <number x> and a real <number y>, outline returns an image where edge pixels are set to the value x and non-edge pixels are set to the value y. Pixel (i, j) is an edge pixel iff its value is different than the value of either pixel (i, j+1) or pixel (i+1, j). The default value of <number x> is one and < number y> is zero. > (outline binary-stop) #<image: rows = 86 cols = 159> >

  

• (label <image>) Given a binary <image>, label returns an image where pixels in distinct connected components (based on 4-neighbor connectivity) have distinct integer values. These values range from 1 to n where n is the number of connected components in <image>. > (make-hot-image (label binary-stop)) #<color-image: rows = 86 cols = 159> >

  

  > (fold max (label binary-stop)) 4 >
• (distance-transform <image>) Given a binary <image>, distance-transform returns an image representing the 2D distance transform of <image>. For example, > (distance-transform (dilate binary-stop)) #<image: rows = 86 cols = 159> >

  

• (open <image> . <array>) Given a binary <image>, and an <array> consisting solely of zeros and ones representing a structuring element, erode returns the morphological opening of <image> with the structuring element. The default value of <array> is #(#(1 1) #(1 1)). For example, > (open noisy-stop) #<image: rows = 86 cols = 159> >

  

• (close <image> . <array>) Given a binary <image>, and an <array> consisting solely of zeros and ones representing a structuring element, close returns the morphological closing of <image> with the structuring element. The default value of <array> is #(#(1 1) #(1 1)). For example, > (close noisy-stop) #<image: rows = 86 cols = 159> >

  

  > (open (close noisy-stop)) #<image: rows = 86 cols = 159> >

  

• (areas <image>) Given integer <image>, areas returns a vector where the n-th component equals the number of pixels with value n. If <image> is the result of applying label to a binary image, then the vector represents the areas of the connected-components of the binary-image. If not, areas returns the grey-level histogram of the image. For example, > (areas (label binary-stop)) #(9676 1039 1205 718 1036) >
• (perimeters <image>) Given integer <image>, perimeters returns a vector where the n-th component equals the number of pixels with value n which are adjacent to pixels of value 0 and the 0-th component equals the sum of the other components. If <image> is the result of applying label to a binary image, then the vector represents the perimeters of the connected-components of the binary-image. For example, > (perimeters (label binary-stop)) #(1082 314 326 190 252) >
• (centers-of-mass <image>) Given <image>, the result of applying label to a binary-image, centers-of-mass returns a vector where the n-th component is a two element list representing the average row and column indices of pixels of the n-th connected-component of <image>. For example, > (centers-of-mass (label binary-stop)) #((43.9084 79.3117) (42.2127 24.7055) (41.6788 92.2241) (35.1393 57.4624) (35.6902 130.086)) >
• (bounding-boxes <image>) Given <image>, the result of applying label to a binary-image, centers-of-mass returns a vector where the n-th component is a four element list representing the minimum and maximum row and column indices of pixels of the n-th connected-component of <image>. For example, > (bounding-boxes (label binary-stop)) #((0 0 85 158) (10 24 73 27) (10 89 73 96) (11 44 72 61) (12 118 72 125)) >