When people express frustration, they sometimes emit a sound that English-speakers would spell "argh". The problem with the written transcription is that it is impossible to express the richness and emotion of the utterance. Writers have taken to using capital letters or longer versions of the word for emphasis, e.g. "ARGHHHH" or "AARRRGH!" I am interested in the variations of the number of letters people use to express this word. It consists of four different letters, each of which can be repeated an arbitrary number of times. Since writers rarely permute the ordering of the letters (e.g. "ARGHGR!"), most instances of "argh" can be expressed as a 4-tuple, where each value is the number of times each letter is repeated. So "argh" is (1,1,1,1), "aargh" is (2,1,1,1), and so on. These tuples can also be thought of as coordinates on a tesseract, or 4-dimensional hypercube.
The argh-scape is the 4-dimensional matrix representing the observed frequencies of the variants of the written word "argh". Each index of the matrix represents one of the four letters, and the matrix entries contain the frequencies with which the corresponding spelling is used. I used Google's search engine to estimate these frequencies in the World Wide Web's content.
Because the space is 4-dimensional, it is not obvious how to visualize it. One can present summary statistics or take two- and three- dimensional "slices" of the hypercube. I took a few small samples of argh-space from Google (small so as not to annoy the Google sysadmins again), and I will try to convey this information to you. My main source of data is one 4x4x4x4 sample, a few 8x8 slices, and several 1-dimensional transects of argh-space on Google.
| spelling | # of hits on Google |
|---|---|
| argh | 121000 |
| aargh | 18600 |
| arrgh | 15700 |
| aaargh | 15500 |
| arrrgh | 10200 |
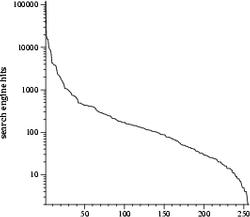
I believe these to be the five most common spellings of "argh". The longer variants drop in frequency rapidly. The graph below is the ranked frequency distribution of the 256 arghs in the 4x4x4x4 corner of argh-space which encompasses all spellings of argh that contain 4 or fewer of each letter. Note that the y-axis is log scale.

The flatness in the middle of the curve is probably due to the fact that the 4x4x4x4 tesseract has only one word with length 4 ("argh"), one of length 16 ("aaaarrrrgggghhhh"), and the most words of intermediate length, which likely have similar frequencies.
The 4 one-dimensional transects fix three of the coordinates at 1, while varying the remaining coordinate. Thus, one of the transects samples "argh", "aargh", "aaargh", etc., while another traverses "argh", "arrgh", "arrrgh", and so on. The plots below are the frequencies sampled along these transects.
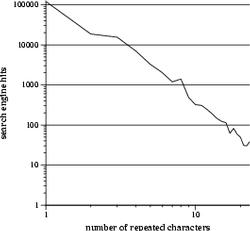 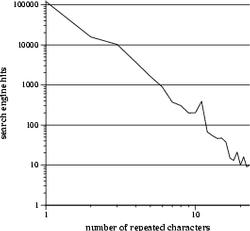 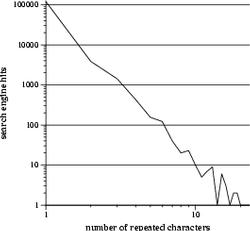 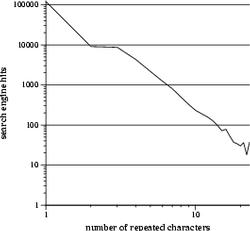 |
These plots provide a rough idea of which letters are more likely to be repeated. The curves approximately follow an exponential decay (thank god it's not a power law), and, judging from the slopes, "a" and "h" decay the slowest, followed closely by "r", and "g" takes a distant fourth. In other words, people are more likely to write "aaaaaaaargh" than "arggggggggh", which looks stupid.
I took six 8x8 2-dimensional slices of the argh-scape, keeping the numbers of two letters fixed at 1 and varying the number of the remaining two. The red squares represent high values, blue low, and gray intermediate. Brightnesses in all plots are scaled the same. The axes represent the number of one of the letters varying. For the first plot: the top left corner is "argh", the bottom left corner is "aaaaaaaargh", and the bottom right is "aaaaaaaarghhhhhhhh", which was found only once by Google. The brightest red square in all plots represents coordinate (1,1,1,1), the word "argh".

| A 
A 

R 
G 
|
The values along the axes appear to be higher than their neighbors, implying that people typically pick one letter to repeat and only type one of each of the other three.
If there were only three plots, they could be attached along their common edges to form the faces of half a cube. As there are six, they would form three inverted half-cubes that meet at one corner.