Modelli del Disco e del Semipiano

1 Modelli in Geometria Iperbolica

I modelli hanno, in primo luogo, una motivazione di natura logica. Oltre a questo essi risultano utili quando si vanno ad esplorare le proprietà geometriche del piano iperbolico. Il software NonEuclid supporta due differenti modelli del piano iperbolico ossia il modello del Disco e quello del Semipiano. Ciascuno dei due modelli può essere selezionato dal menu "Visualizza" selezionando le opzioni "Disco" o "Semipiano". Gli oggetti geometrici sono visivamente diversi nei due modelli. Nel modello del disco le rette sono di due tipi o archi di circonferenza perpendicolari alla circonferenza limite o segmenti passanti per il centro della circonferenza limite. Nel modello del semipiano le rette sono o semicirconferenze con centro sulla frontiera del semipiano o rette perpendicolari a quest'ultima. All'interno di un modello abbiamo una certa libertà di definire "punti", "rette", "distanze" "angoli" ... tuttavia dobbiamo dimostrare che le scelte che operiamo non contraddicono gli assiomi della geometria iperbolica.

2 Il modello del Disco di Poincaré

Per sviluppare il modello del disco di Poincaré consideriamo, nel piano, un cerchio C. Possiamo assumere, senza perdita di generalità, che il raggio di C sia unitario.

Figure 8.1: Rette nel modello del Disco

Sia C* una qualsiasi circonferenza perpendicolare a C ossia C e C* hanno tangenti perpendicolari
nei loro punti di intersezione. Nel seguito indichiamo con D-punto, D-retta, ecc... punto, retta ecc... nel modello del disco.

D-punti: sono i punti euclidei interni a C. Indichiamo l'insieme di questi punti con D°.

D-rette: possono essere di due tipi (1) intersezioni di C* con D° o (2) intersezioni di diametri di C con D°.

Le D-rette definite in questo modo rendono possibile che la teoria sia consistente con gli assiomi della geometria iperbolica. Tra questi assiomi uno stabilisce che dati due D-punti distinti esiste una sola retta passante per essi. Non è difficile convincersi della validità di questo assioma in relazione alla scelta fatta della tipologia delle rette. In Appendice A si mostra come si determina l'equazione di una circonferenza euclidea una volta assegnati due punti e il centro. Un secondo assioma della geometria iperbolica afferma che: "Ogni segmento può essere prolungato". Questo assioma è soddisfatto anche se il modello del disco è limitato. Infatti le D-rette sono topologicamente aperte per cui i D-punti ad esse appartenenti possono avvicinarsi a piacere a C senza tuttavia giacere su C. In altri termini fissato su una D-retta un D-punto "vicino" a C è sempre possibile determinare un ulteriore D-punto sulla retta "più vicino" a C del precedente.

Nel modello del disco possiamo definire una distanza che gode delle seguenti proprietà generali:

la distanza d(PQ) è definita per ogni coppia di D-punti P e Q.

d(PQ) = 0 se e solo se P e Q coincidono altrimenti la distanza è positiva.

d(PQ) = d(QP) ossia la D-distanza di P da Q è uguale alla D-distanza di Q da P.
Una linea retta individua il cammino di lunghezza minima tra i punti due punti che la individuano. In altri termini vale la "disuguaglianza triangolare" d(AC) <= d(AB) + d(BC), dove A, B e C sono tre D-punti qualsiasi.
La distanza è continua e fissato un qualsiasi numero positivo x esiste almeno una coppia di D-punti P e Q tali che d(PQ) = x. Ciò in accordo con l'assioma che afferma: "Si possono costruire circonferenze di qualsiasi centro e raggio".

D-distanza: Siano P e Q due D-punti. Essi individuano univocamente una D-retta che, al limite, interseca C in due punti euclidei A e B (vedi figura 8.1). Facciamo notare che A e B non sono D-punti in quanto appartengono a C. Siano |PA|, |PB|, |QA|, e |QB| le distanze euclidee P da A, ecc. e sia ln il logaritmo naturale. Allora definiamo la D-distanza tra i punti P e Q come:

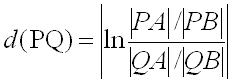
Una dimostrazione del fatto che la distanza scelta soddisfa tutte le precedenti proprietà può essere trovata in E.E. Moise's "Elementary Geometry from an Advanced Standpoint" [Moise-74].

D-circonferenze: una D-circonferenza è definita come il luogo dei punti del piano iperbolico equiD-distanti da un D-punto fissato.

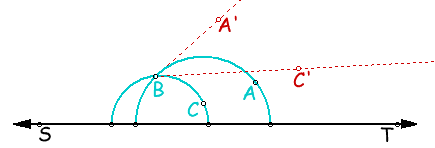
D-ampiezza di un D-angolo: consideriamo l'angolo di figura 8.2. Le rette BA' e BC' sono tangenti (in senso euclideo) agli archi AB e BC. Per definizione la D-ampiezza dell'angolo iperbolico coincide con l'ampiezza euclidea dell'angolo formato dalle rette tangenti BA' e BC'.

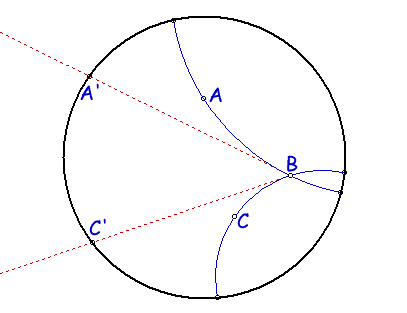
Figure 8.2: Ampiezza di un D-angolo.

3 Il modello del Semipiano

Per introdurre il modello del semipiano consideriamo innanzitutto un retta ST nel piano.

H-punti: sono i punti euclidei interni al semipiano superiore delimitato da ST. Indichiamo l'insieme di questi punti con H.

H-rette: possono essere di due tipi (1) intersezioni di circonferenze con centro appartenente ad ST con H o (2) intersezioni di rette perpendicolari a ST con H.

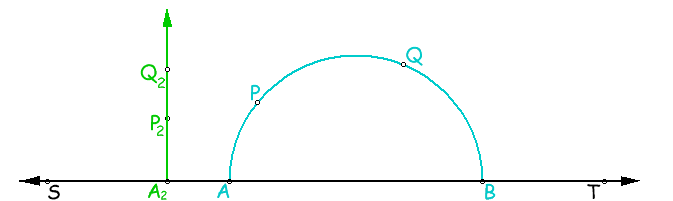
Figure 8.3: Rette nel modello del Semipiano

H-distanza: siano P e Q due H-punti. Supponiamo che essi individuino univocamente una H-retta di tipo (1) che, al limite, interseca ST in due punti euclidei A e B (vedi figura 8.3). Facciamo notare che A e B non sono H-punti in quanto appartengono a H. Siano |PA|, |PB|, |QA|, e |QB| le distanze euclidee P da A, ecc. Sia ln il logaritmo naturale. Allora definiamo la D-distanza tra i punti P e Q come in 8.3.1. Nel caso in cui i punti definiscano una H-retta del tipo (2) (vedi figura 8.3) la distanza si determina attraverso la relazione 8.3.2.

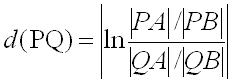(8.3.1) 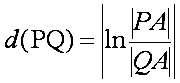(8.3.2)

H-circonferenza: una H-circonferenza è definita come il luogo dei punti del piano iperbolico equiH-distanti da un H-punto fissato.

H-ampiezza di un H-angolo: consideriamo l'angolo della figura sottostante. Le rette BA' e BC' sono tangenti (in senso euclideo) agli archi AB e BC. Per definizione la H-ampiezza dell'angolo iperbolico coincide con l'ampiezza euclidea dell'angolo formato dalle rette tangenti BA' e BC'.

Appendice A

Problema: dati due punti P=(Px, Py) e Q=(Qx, Qy) interni al cerchio unitario C con centro coincidente con l'origine del piano cartesiano (O,x,y) determinare l'equazione della circonferenza C* perpendicolare a C.

Soluzione: siano (Xo,Yo) le coordinate del centro di C*. Dal momento che i punti P e Q giacciono su C* si hanno le equazioni:

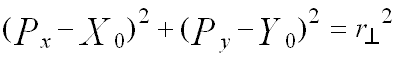(equazione A.1)
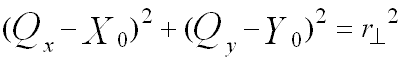(equazione A.2)

Essendo le circonferenze ortogonali il segmento che congiunge i loro centri coincide con l'ipotenusa di un triangolo rettangolo che ha per cateti i raggi di C e C*. Per il teorema di Pitagora si ha:

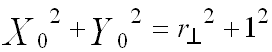(equazione A.3)

Sviluppando A.1 e usando A.3 si ottiene:

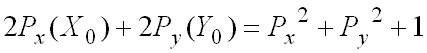(equazione A.4)

Sviluppando A.2 e usando A.3 si ottiene:

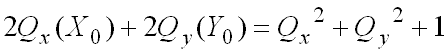(equazione A.5)

Il sistema di equazioni A.4 e A.5 è lineare in Xo e Yo essendo i rimanenti termini costanti. Si ha una soluzione sole se il determinante della matrice dei coefficienti è non nullo ossia se:

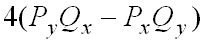(equazione A.6)

è diverso da zero. Questa condizione non è soddisfatta solo se i due punti appartengono ad una retta passante per l'origine (un diametro di C). Nel caso in cui i punti P e Q non giacciano su un diametro di C le equazioni A.4 e A.5 possono essere risolte per determinare il centro (Xo,Yo) della circonferenza ortogonale.

Pagina Iniziale
Successivo - Per l'insegnante: perchè studiare geomeria iperbolica?