10: Disk and Upper Half-Plane Models of Hyperbolic Geometry

10.1 Models of Hyperbolic Geometry:
Models serve primarily a logical purpose. They are useful when exploring the geometric properties of the hyperbolic plane; they don't "look like" the hyperbolic plane. NonEuclid supports two different models of the hyperbolic plane: the Disk model and the Upper Half-Plane model. A given figure can be viewed in either model by checking either "Disk" or "Upper Half-Plane" in the "model" command of the "View" menu. The figure will look differently in each of the models, but its geometric properties (segment lengths, angle measures, area, and perimeter) will be the same. In the disk model, a line is defined as an arc of a circle that is orthogonal to the unit circle. In the Upper Half-Plane model, a line is defined as a semicircle with center on the x-axis. It must be remembered that neither of these are what lines "are" in hyperbolic geometry. We can define "points", "lines", "distance" and "angles" as anything we want. If we can prove that the relations that exist among these "points", "lines", "distance" and "angles" satisfy all the axioms of the hyperbolic plane, then we have a model of the hyperbolic plane.

10.2 The Poincaré Disk Model:
To develop the Poincaré disk model, consider a fixed circle, C, in a Euclidean plane. We assume, without loss of generality, that the radius of C is 1, and that its center is at the origin of the Euclidean plane.

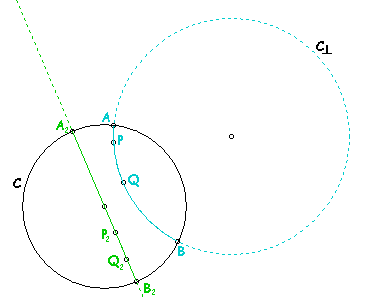
Figure 10.1: Lines in the disk model.

Let C⊥ be any circle which is orthogonal to circle C. Two circles are orthogonal when their tangents at each intersection point are perpendicular. In the following discussion, D-points, D-lines, etc. are used to identify how points, lines, etc. are defined in the disk model.

D-points: D-points are Euclidean points of the interior of C. Let Ω denote the set of all D-points.

D-lines: A D-line is either (1) the intersection of Ω and C⊥, or (2) the intersection of Ω and a diameter of C.

D-lines, defined in this way, are consistent with the axioms of hyperbolic geometry. One of the axioms of hyperbolic geometry states that every two D-points lie on exactly one D-line. By trying a few sketches on paper, you can get an intuitive feel for why this axiom is upheld by the above definition of D-lines. Appendix A shows how to find the Euclidean equation of circle unlikely determined by any two D-points. Another axiom of HG is: "Any line segment with given endpoints may be continued in either direction". This axiom is satisfied even though the points in the disk model are bounded by the unit circle. Notice that D-lines form open intervals (D-points may be arbitrarily close to C, but may not actually be on C). Therefore, no matter now close an endpoint is to C, it can always be made a little closer.

The disk model also includes a distance function. Before stating this function, consider what properties it must satisfy:

The distance function, d(PQ), must be defined for all pairs of D-points, P and Q.
d(PQ) = 0 if P and Q are the same D-point, and is a positive number otherwise.
d(PQ) = d(QP) - in other words, the D-distance from P to Q must be the same as the D-distance from Q to P.
A straight line should be the shortest D-distance between two D-points. This is called "the triangle inequality" and can be stated symbolically. For all triples of D-points, A, B, and C, d(AC) ≤ d(AB) + d(BC).
The distance function must be continuous, and for any positive real number, x, there must be at least one pair of D-points, P and Q, such that d(PQ) = x. This is required by Euclid's third axiom: "It is possible to construct a circle with any point as its center and with a radius of any length".

D-distance: Let P and Q denote two D-points. These D-points determine a unique D-line that approaches the boundary circle, C, in two Euclidean points, A and B (see figure 10.1). Notice that A and B are not D-points since they are on the boundary circle. Let |PA|, |PB|, |QA|, and |QB| denote the Euclidean distances from point P to A, etc. Let Ln denote the natural logarithm. The D-distance between D-points, P and Q, is defined as:

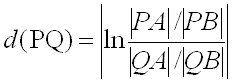
A formal development of this function, and proof that it satisfies the criteria listed above can be found in E.E. Moise's "Elementary Geometry from an Advanced Standpoint" [Moise-74].

D-circles: A D-circle is defined as the set of all D-points that are equal D-distance from a given D-point.

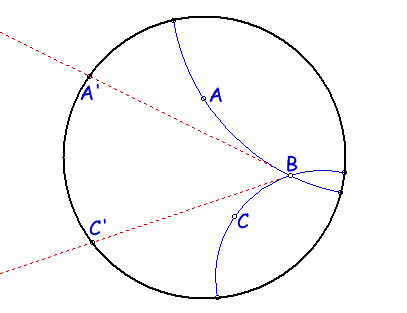
D-angle measure: Given three D-points, A, B, and C, construct the Euclidean rays BA' and BC' that are tangent to D-lines BA and BC at point B (see figure 10.2). The measure of D-angle, ABC, is defined as equal to the measure of Euclidean angle, A'BC'.

Figure 10.2: The Measure of a D-angle is the Measure of the Euclidean Angle formed by the Tangent Rays.

10.3 The Upper Half-Plane Model:
To develop the Upper Half-Plane model, consider a fixed line, ST, in a Euclidean plane. We assume, without loss of generality, that ST is on the x-axis of the Euclidean plane.
H-points: H-points are Euclidean points on one side of line ST. Let Ψ denote the set of all H-points.

H-lines: An H-line is either (1) a semicircle within Ψ, and with center on ST, or (2) the intersection of Ψ and a perpendicular to ST.

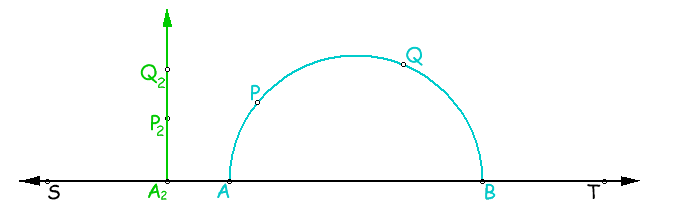
Figure 10.3: Lines in the Upper Halp-Plane Model.

H-distance: Let P and Q denote two H-points. If the unique H-line that passes through these two points is a semicircle, then the H-line approaches the boundary line, ST, in two Euclidean points, A and B, and the distance between P and Q, d(PQ), is given by equation 10.3.1. If the unique H-line that passes through these two points is a line, then the H-line approaches the boundary line, ST, in one Euclidean points, A₂, and the distance between P and Q, d(PQ), is given by equation 10.3.2. In both equations 10.3.1 and 10.3.2, Let |PA|, etc. denote the Euclidean distances from point P to A, etc. Let Ln denote the natural logarithm.

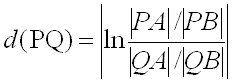(10.3.1)

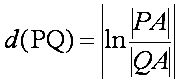(10.3.2)

H-circles: A H-circle is defined as the set of all H-points that are equal H-distance from a given H-point.

H-angle measure: Given three H-points, A, B, and C, construct the Euclidean rays BA' and BC' that are tangent to D-lines BA and BC at point B (see figure 10.4). The measure of H-angle, ABC, is defined as equal to the measure of Euclidean angle, A'BC'.

Appendix A:

Problem: Given two points P=(Px, Py) and Q=(Qx, Qy) on the interior of the unit circle, C, with center at the origin of a Cartesian coordinate system, find the equation of the Circle, C⊥ which is orthogonal to C.

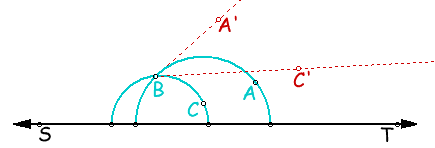
Solution: Let (Xo,Yo) be the coordinates of the center of C⊥, and let r⊥ be the radius. Since the two points P and Q lie on C⊥, we have the following two equations:

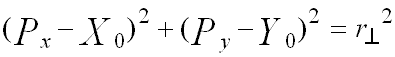(equation A.1)

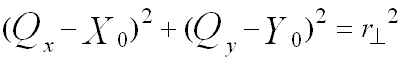(equation A.2)

Since the two circles are orthogonal, the line segment joining the two centers forms the hypotenuse of a right triangle with one leg a radius of C and the other a radius of C⊥. Thus, the Pythagorean theorem gives:

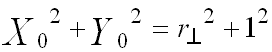(equation A.3)

Expending equation A.1 and using equation A.3 gives:

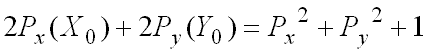(equation A.4)

Expending equation A.2 and using equation A.3 gives:

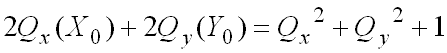(equation A.5)

Equations A.4 and A.5 are linear equations in Xo and Yo since the other variables are fixed. There will be a solution when the determinant of coefficients is non zero, that is, if and only if:

(equation A.6)

is non zero. The determinant is not zero if and only if the two points lie on a line through the origin (a diameter of C). When the two points, P and Q, do not lie on a diameter of C, equations A.4 and A.5 can be easily solved to give the center (Xo,Yo) of the orthogonal circle.