7: Axioms and Theorems

All of Euclidean geometry (the thousands of theorems) were all put together with a few different kinds of blocks. These are called "Euclid's five axioms":

• A-1 Every two points lie on exactly one line.
• A-2 Any line segment with given endpoints may be continued in either direction.
• A-3 It is possible to construct a circle with any point as its center and with a radius of any length. (This implies that there is neither an upper nor lower limit to distance. In-other-words, any distance, no mater how large can always be increased, and any distance, no mater how small can always be divided.)
• A-4 If two lines cross such that a pair of adjacent angles are congruent, then each of these angles is also congruent to any other angle formed in the same way.
• A-5 (Parallel Axiom): Given a line l and a point not on l, there is one and only one line which contains the point, and is parallel to l.

In addition to its axiom, Euclidean geometry is based on a number of common notions that Euclid listed in "The Elements". Unlike the axioms which deal with objects of geometry, the common notions are general rules of logic:

• CN-1  Things which are equal to the same thing are also equal to one another.
• CN-2  If equals be added to equals, the wholes are equal.
• CN-3  If equals be subtracted from equals, the remainders are equal.
• CN-4  Things which coincide with one another are equal to one another.
• CN-5  The whole is greater than the part.

Euclid's goal was for these axioms and common notions to be (1) few in number, and (2) so obviously true that they could not possible be argued with. For over 2000 years, many mathematicians believed that the fifth axiom (the Parallel Axiom) was not needed. They believed that it could instead be proved as a theorem of the first four axioms. There were numerous attempts to do so. Early in the nineteenth century, three men working independently, finally put an end to this impossible search. These men were Ivanovitch Lobachevski in Russia, Karl Gauss in Germany, and János Bolyai in Hungary. These men each developed theorems using Euclid's first four axioms and a negation of the Parallel Axiom. Their expectation was to eventually develop two theorems which contradicted each other. This would prove that their negation of the Parallel Axiom is inconsistent with the first four axioms - thereby proving the Parallel Axiom (and making it the Parallel Theorem). To their surprise, however, they never obtained a contradiction. Instead, they developed a complete and consistent geometry - a non-Euclidean geometry that is now called hyperbolic geometry. This proved that the Parallel Axiom could not be derived from the other four.This was of great mathematical and philosophical interest. From the time of the Greeks, it was believed that geometric theorems were such pure and perfect Truth that they did not need to be scrutinized by observations of the real world. Now, those statements are only true is some geometries. The only reason to prefer one geometry over another is by comparison to the real world - a heavy blow to a geometor. In the early twentieth century, Albert Einstein developed The General Theory of Relativity which made extensive use of hyperbolic geometry. Thus, abstract, mathematical philosophy was now firmly in the realm of Science.

There are actually two ways to negate the Euclidean Parallel Axiom:

• A-5S (Spherical Geometry Parallel Axiom): Given a line l and a point not on l, no lines exist that contain the point, and are parallel to l.
• A-5H (Hyperbolic Geometry Parallel Axiom): Given a line l and a point not on l, there are at least two distinct lines which contains the point, and are parallel to l.

When thinking about these parallel axioms, it is important to remember that "parallel" does not mean "lines that look like train tracks". "Parallel" means two lines in the same plane that, no matter how far extended, do not intersect.

The Spherical Geometry Parallel Axiom is inconsistent with Euclid's first four axioms. In spherical geometry, The "lines" are great circles. Most pairs of points (A and B) in spherical geometry, lie on one and only one great circle; however if A and B happen to be antipodal (on opposite ends of any single axis), then there are an infinite number of different great circles that pass through them. This violates Euclid's first axiom. Euclid's second axiom, "any line segment with given endpoints may be continued in either direction" is also violated. In spherical geometry, if points the endpoints of a line segment are moved farther and farther apart, then they will eventually coincide.

Contrary to Lobachevski's, Bolyai's, and Gauss' expectations, the hyperbolic geometry Parallel Axiom is perfectly consistent with Euclid's first four axioms. And what a beautiful world this surprise opened up.

7.2 Betweeness and SAS Axioms:
In addition to the axioms and common notions that Euclid included in "The Elements",  he unknowingly made a number of implicit assumptions.  One of these is called the Betweeness Axiom and can be stated: "Of any three points on a line, exactly one is between the other two." Another is called the SAS (or Side-Angle-Side) Axiom.

The SAS axiom states that if two sides and the included angle of one triangle are congruent to two sides and an included angle of a second triangle, then the two triangles are congruent.

In "The Elements", Euclid presents what he believed to be a proof for SAS:[Health-56]

Given:
ABC and DEF, with sides AB DE, side AC DF, and A D.

Proof:

Move ABC such that point A coincides with point D, and line AB coincides with DE.
Point B will coincide with E, because AB DE.
Also, segment AC will coincide with DF, because A D.
Point C will coincide with F, because AC DF.
Line BC will coincide with EF, because two lines cannot enclose a space.
Finally, side BC is congruent to side EF, because the lines and endpoints of each coincide.
Therefore, B E, C F, and ABC DEF.

7.3 Proofs in Hyperbolic Geometry:
Euclid's 5 axioms, the common notions, plus all of his unstated assumptions together make up the complete axiomatic formation of Euclidean geometry. The only difference between the complete axiomatic formation of Euclidean geometry and of hyperbolic geometry is the Parallel Axiom.

This is a powerful statement. It means that any proof in Euclidean geometry which does not use the Parallel Axiom is also a proof in hyperbolic geometry!

Likewise, it means that Euclidean geometry theorems that require the Parallel Axiom will be false in hyperbolic geometry. A striking example of this is the Euclidean geometry theorem that the sum of the angles of a triangle will always total 180°. Figure 7.3a may help you recall the proof of this theorem - and see why it is false in hyperbolic geometry.

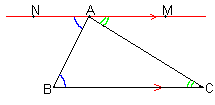
Figure 7.3a: Proof for mA + mB + mC = 180°

In Euclidean geometry, for any triangle ABC, there exists a unique parallel to BC that passes through point A. Additionally, it is a theorem in Euclidean geometry that when two parallel lines are cut by a transversal, then the opposite interior angles are congruent; therefore, NAB ABC and MAC ACB. In gyperbolic feometry, however, there are an infinite number of lines that are parallel to BC and pass through point A, yet there does not exist any line such that both: NAB ABC and MAC ACB.

7.4 Angle Measure Axioms: The ancient Greeks considered that measurement was merely one of the practical arts. It was considered unworthy of the attention of mathematicians and philosophers. Moderen Geometery, however,