4: The Shape of Space

1. Matter and energy distort space, and
2. The distortions of space affect the motions of matter and energy.

Some people say that Time is the 4th dimension. This is, in a sense, true. However, time is not the "different direction" of which I was speaking. If we want to count time as a dimension, then we should say that we live in a four dimensional space-time that is curved into the 5th dimension! So where is this "different direction"?

4.2 Flatland
It is very difficult to visualize four dimensions of space. In 1884, a Victorian schoolmaster, Edwin Abbott, published a book about an imaginary two-dimensional world called Flatland.  Flatland is inhabited by creatures that slide about.  We might think of them as being like coins on a tabletop. Alternatively, we could think of them as colored patterns in a soap film. The story focus on the adventures of A Square, Flatland's most famous citizen, and his path to an understanding of the third dimension. 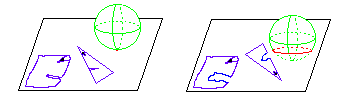By thinking about A Square's difficulties in understanding the third dimension, we become better able to deal with our own problems with the fourth dimension. Early in the story, A Square and his wife are comfortably sealed up in the safety of their home, when suddenly a voice out of nowhere speaks to them. And then, a moment later, a circle appears in the confines of their tightly locked house. It is A Sphere, come to teach A Square about the third dimension:

"I am not a plane Figure, but a Solid. You call me a Circle; but in reality I am not a Circle, but an indefinite number of Circles, of size varying from a Point to a Circle of thirteen inches in diameter, one placed on the top of the other. When I cut through your plane as I am now doing, I make in your plane a section which you, very rightly, call a Circle. For even a Sphere - which is my proper name in my own country - if he manifest himself at all to an inhabitant of Flatland - must needs manifest himself as a Circle." [Abbott-1884]

4.3 Ourland
This bulging out into the 4th dimension that our universe seems to do occurs on different scales: For example, micro-scale curvature results from each subatomic particle. Medium-scale curvature is associated with gravitational attraction of stars, black holes, and galaxies. Large-scale curvature is the overall shape of space, and is the cumulative result of the totality of all the mater and energy in space. To make clear what is meant by different "scales of curvature", consider the following: On the large-scale, we say that the surface of the Earth is curved into the shape of a sphere that bulges a bit at the equator. On the medium, human-sized scale, we notice that the Earth's surface is covered with hills valleys, mountains and planes. On a smaller scale, the Earth's surface breaks into individual rocks and clods of dirt.

It appears that much of our universe has a particular kind of curvature that follows a hyperbolic geometry, yet this is not apparent on the scale that we are accustomed to observing. The surface of the Earth's oceans curve around the globe, yet even as a few square miles of ocean appear flat, a small chunk of hyperbolic geometry approximates Euclidean geometry. For example a triangle formed by three points of light in a classroom on Earth has an angle sum so near 180 degrees that any difference is too small for us to notice (the sides curve inward by a very tiny amount). Thus, it usually appears we live in a Euclidean geometry; however, triangles defined by a set of three distant stars can have angle sums measurably different from 180 degrees.

Even on a large scale, there are many commonalities between hyperbolic geometry and Euclidean geometry, such as the base angles of isosceles triangles being congruent, but, on the large scale, there are also striking differences.

4.4 Mercury's Orbit
The distance from the Earth to the Sun is much too small for our most sensitive instruments to measure any of the differences between Euclidean and hyperbolic geometry caused by the large-scale curvature of space. However, our Sun causes some medium-scale curvature that - thanks to planet Mercury - we are able to measure. Mercury is the closest planet to the Sun. It is in a much higher gravitational field than is the Earth, and therefore, space is significantly more curved in its vicinity. Mercury is close enough to us so that, with telescopes, we can make accurate measurements of its motion. Mercury's orbit about the Sun is slightly more accurately predicted when hyperbolic geometry is used in place of Euclidean geometry.