2: Using NonEuclid - My First Triangle

NonEuclid an interactive, two-dimensional, model of a particular Non-Euclidean geometry called hyperbolic geometry. The default model used by NonEuclid is called the Poincaré Model. The Poincaré model resides inside a circle called the "Boundary Circle". This is the large circle that appears when you first start NonEuclid. The inside of this boundary circle is the graphing area of the screen and it models the entire, infinite, two-dimensional hyperbolic plane.

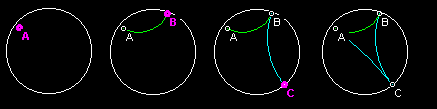The hyperbolic geometry triangle, ABC, shown above looks bent. Actually, the three sides that make it up are, in hyperbolic geometry, perfectly straight lines! Most straight lines in hyperbolic geometry appear curved when viewed from our normal Euclidean geometry. If you could somehow be transported inside a world of Hyperbolic Geometry, then all of the "straight lines" shown in this simulation would appear perfectly straight to your vision.

The following steps lead you through the construction of the hyperbolic geometry triangle.

Select the "Draw Line Segment" option from the "Constructions" Menu. This will cause the "Draw Line Segment" Dialog to appear.
Move the mouse inside the boundary circle.
Click the mouse somewhere inside the boundary circle. This will cause a point to be plotted. After plotting this first point, notice that as you move the mouse inside the boundary circle "Length = " followed by a number is printed in a text box within the "Draw Line Segment" dialog box. This length is the distance from the first point you plotted to the current location of the mouse.
Click the mouse in a second place inside the boundary circle. This will cause a second point to be plotted and a straight line to be drawn between the two points.
Click the mouse on one of the endpoints of your new line segment. Then move the mouse to a third point and click again. This will cause a second straight line segment to be drawn. Two sides of your triangle are now complete.
Construct the third side by clicking on the two open endpoints. Your first hyperbolic geometry triangle is now complete.
You can now measure angles and the length of the sides of your triangle by selecting the "Measure Triangle" command from the "Measurements" Menu. Notice that the sum of the three angles of your triangle is LESS THEN 180°.

More Exercises for Getting Started:
Now that you have successfully constructed and measured a triangle, it would be a good idea to get a "feel" for this strange geometry. Construct lots of lines and see if you can notice any patterns. Some straight, Hyperbolic Lines appear to be very curved, and others appear almost perfectly straight. Can you predict which pairs of points will determine straight looking straight, hyperbolic lines, and which will produce curved looking straight, hyperbolic lines? Do straight, hyperbolic lines appear curve toward the center, toward the boundary or sometimes toward the center and sometimes toward the boundary? Given two points, try to predict the approximate path of straight, hyperbolic line that passes through them.

Another good way to use NonEuclid is to open your regular high school geometry book to the section called "Constructions With a Straight Edge and Compass". Try to duplicate these constructions in NonEuclid. Some of them will work perfectly (but look quit odd), and others will totally fail. Try to figure out why.

NonEuclid Home
Next Topic - 3: Activities - How to get started Exploring