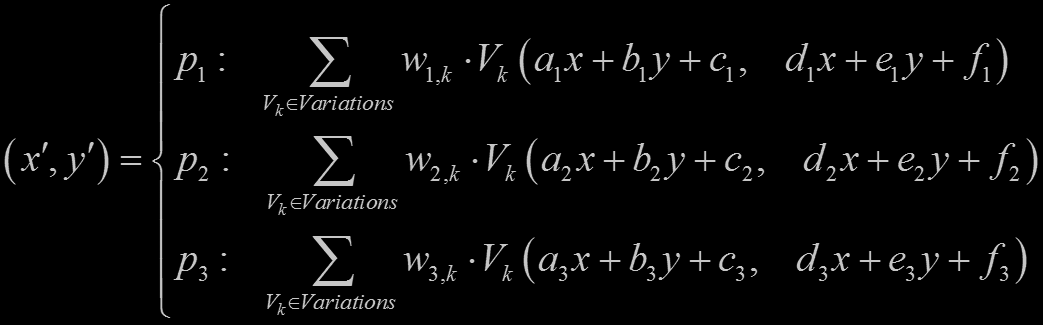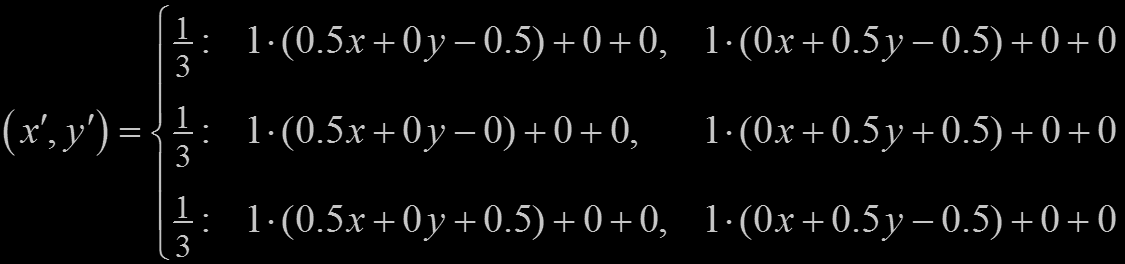Chaos Dancers is a fractal animation. More precisely, each frame is a collection of pixels
representing a mathematical set that exhibits both
self-similarity and differences on endless
magnification. The word "fractal" comes from a curious scaling property that
distinguishes such sets form other geometric
shapes. For example, increasing all the edge lengths of a
polygon by a factor of two will increase the polygon's area by a factor of two raised to the second power.
By contrast, if a fractal's one-dimensional lengths are all doubled, the spatial content of the fractal scales
by two raised to a power that is usually greater than two, and not necessarily an integer. This power, called the
fractal dimension,
differs from one fractal to another (and from one frame of Chaos Dancers to another).
While watching Chaos Dancers, it can be
fun to guess which patterns represent fractals with a relatively high or relatively low fractal dimension.
Chaos Dancers is a type of fractal called an
Iterated Function System mixed with variations and
Circle Inversion.
Chaos Dancers is written using a mix of Javascript, HTML5, CSS, WebGL and GLSL.
The algorithm used here is adapted from the Fractal Flame
developed in 2003 by Scott Draves and Erik Reckase. Draves and Reckase's Fractal Flame algorithm allows for an
an arbitrarily large number of equations and variations. This web app supports only four equations with four variations.
This implementation runs in real-time (60 frames per second on an Intel mobile i5 with a mid level graphics card).
In order to achieve this performance, the original algorithm needed to be modified so as to take advantage of
the massively parallel architecture of modern GPUs. Also, to keep the app real-time, the number of particles per frame
is only twice the number pixels on the canvas (just under a million particles/frame for a 700 x 700 pixels canvas).
While that is a large number of particles, it is vastly less than what is typically used for non-real-time
fractal flame renders.
In addition to the Fractal Flame algorithm, circle inversion, using a single circle that circumscribes the
{(x,y): -1≤ x|y ≤1} view window,
is applied to any particles that would otherwise render outside that circle.
The steps of the algorithm that happen each frame are:
- Javascript modifies the equation coefficients and color tables.
- The modified data together with a large block of random seed particles are loaded into the GPU using
WebGL where each seed particle's "dance" is calculated in a separate instance of a GLSL (OpenGL Shading Language) vertex shader.
- The vertex shader selects one of four transformation equations (see below). The probability of selecting the
ith equation is pi. Each pi is one of the uniforms modified in the
Javascript part of the code and loaded into the GPU each frame.
- The selected transformation equation calculates a new set of coordinates.
- The vertex shader repeats steps (3) and (4) twenty-five times, each time using the result from (4) as the input to (3).
- After the 25 iterations, if a particle is outside the {(x,y): -1≤ x|y ≤1} view window,
then the vertex shader will sometimes (depending on the slider setting)
apply circle inversion to bring the particle back into the viewing area.
- The vertex shader uses the final result from (4) or (5) to calculate a blended color using the color assigned to each equation
weighted by the number of times each equation was chosen. The final coordinates and the blended color are passed to the rasterizer.
- The rasterizer filters any points that are outside the view window, then passes the rest on: each to a different
fragment shader instance. To get an idea of how the blending works, try adjusting the "Color Iterations" slider down to 1 (the lowest setting).
Then, slowly move the slider to 2, 3, 4, ...
- The fragment shader in this program is a single line: it assigns the given color to the given pixel.
In addition to the iteration blending applied in the vertex shader, the fragment shader will use GL Blending
(gl.SRC_ALPHA, gl.ONE_MINUS_SRC_ALPHA) when more than one particle renders to the same pixel.
The three transformation equations in this IFS are:
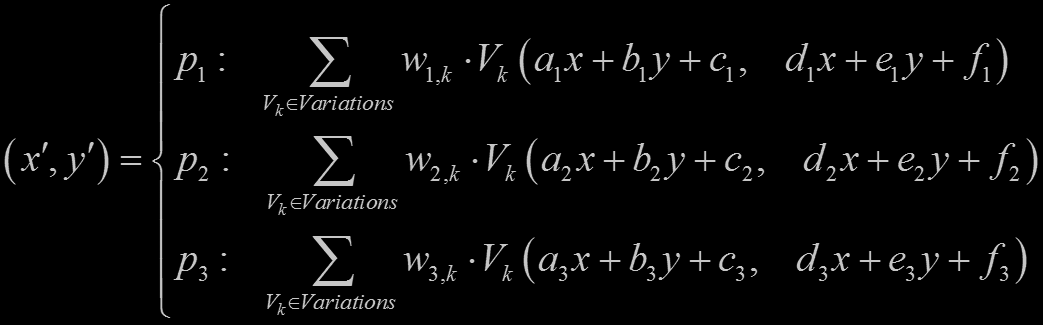
Where p1, p2, and p3 are each the probability that the corresponding
equation is chosen on any one iteration (p1+p2+p3 = 1.0).
Each a, b, c, d, e, and f is a parameter with domain (-1.0, 1.0).
Each parameter wi,k is a weight, in equation i, of the variation Vk.
The variation functions are:
| Linear: |
V1(x, y) = (x, y) |
| Sinusoidal: |
V2(x, y) = (sin(x), sin(y)) |
| Spherical: |
V3(x, y) =
(x/(x2+y2),
y/(x2+y2)) |
| Fisheye: |
V4(x, y) =
(4x/(x2+y2+4),
4y/(x2+y2+4)) |
For the Sierpinski Triangle, only the linear variation function, V1, has a non-zero weight.
Also, the x-coordinate transformation is independent of y and the y-coordinate transformation
is independent of x.
Thus, with vertices {( -1, -1), ( 0, 1 ), ( 1, -1 )} the IFS equation for the Sierpinski Triangle is:
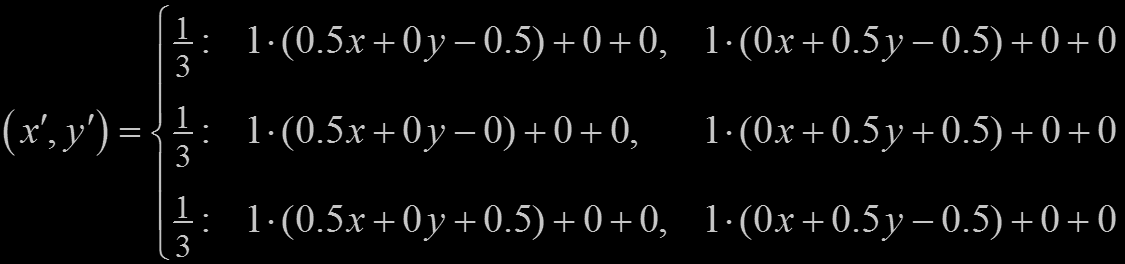
With thanks to Truman DeYoung, Marcos Lemus, and Luke Balaoro for cross-browser / cross-OS testing and for many useful ideas and advice throughout development.