In Search of a Common Scale for Causal Fusion in Neuroimaging
Sergey Plis
joint work with David Danks, Vince
Clark, Andy Mayer, Terran Lane,
Eswar Damaraju,
Mike Weisend, Tom Eichele, Jianyu Yang, and Vince
Calhoun
The Mind Research Network
- definitions
- dangers of unimodal analysis
- a model-based solution
- towards a graph space model fusion
definitions
neuroimaging
- studies brain function
- produces immense amounts of data
- data comes in various forms
- each with their strength and weaknesses
- our goal: use that data to infer causal relations among brain networks
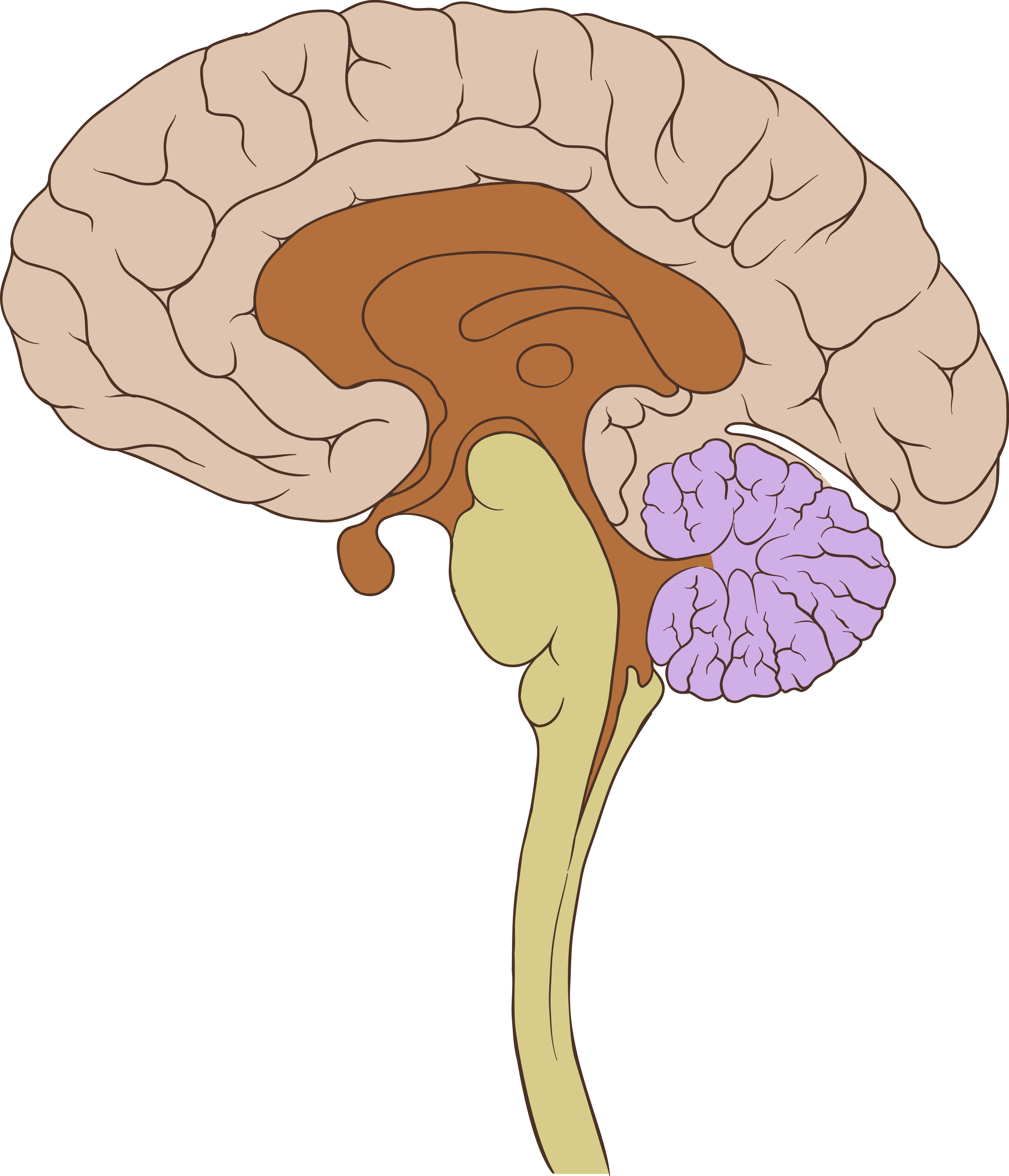
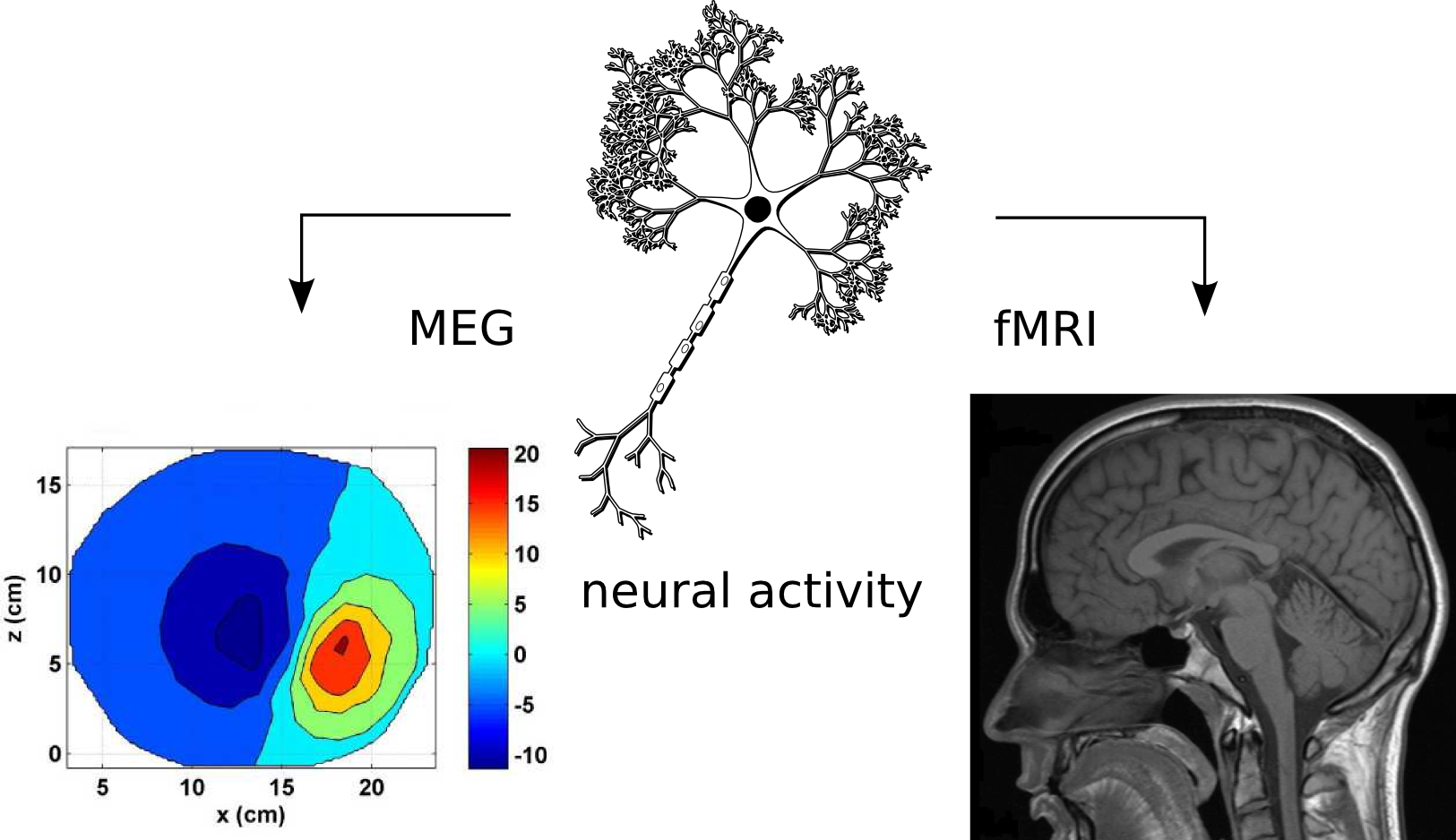
functional MRI
- measures Blood Oxygenation Level Dependent (BOLD) response
- produces 4D data
- Strength: relatively well localized
- Weakness: slow sampling rate
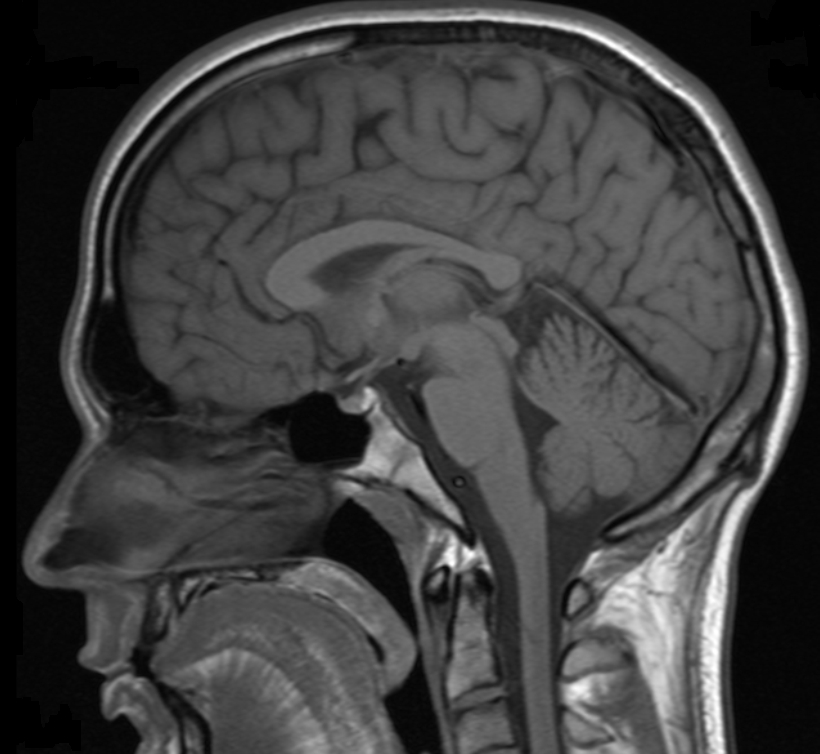
Magnetoencephalography
- measures magnetic field
- Strength: instant reflection of underlying activity
- Weakness: uncertain spatial location

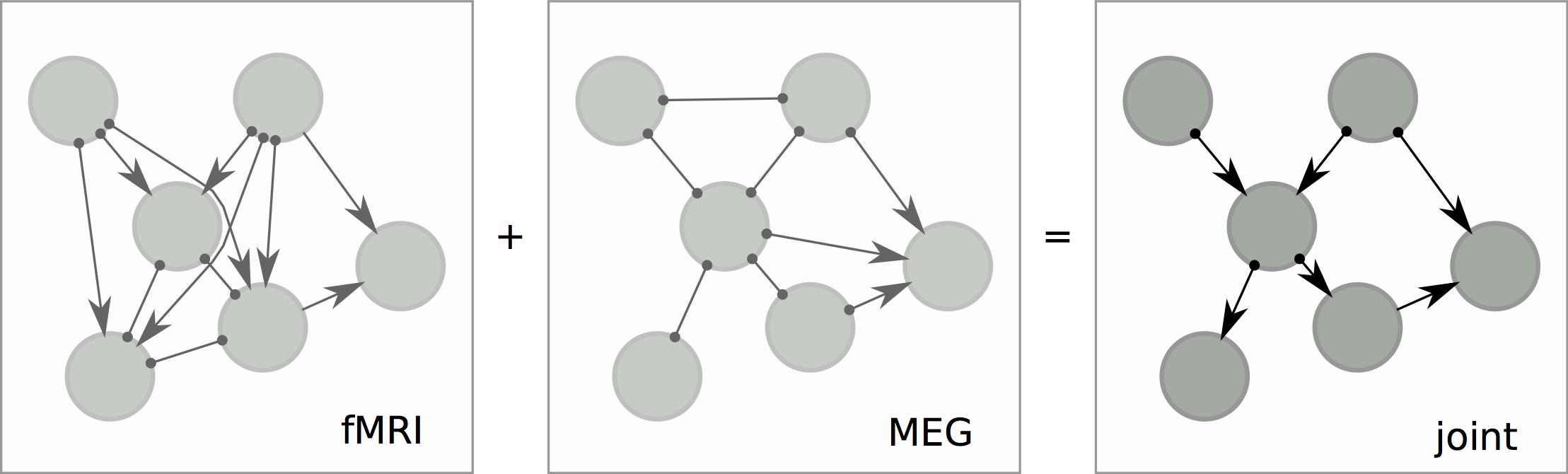
the same underlying phenomena
Bayesian Network
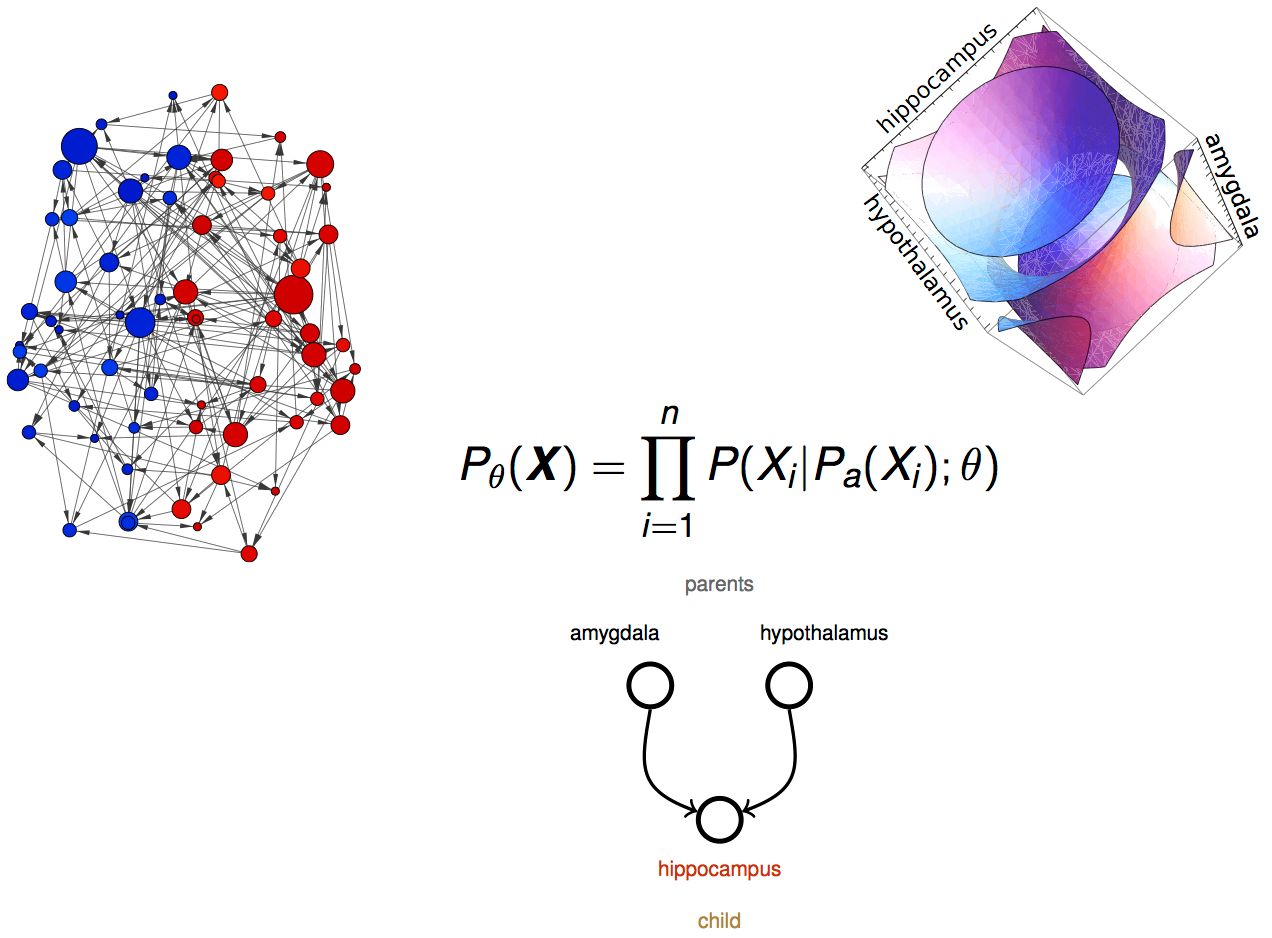
graph characterization

dangers of unimodal analysis
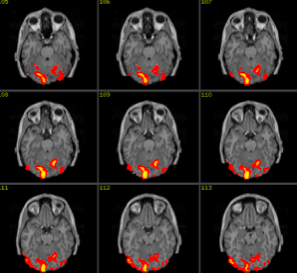
processing pipeline
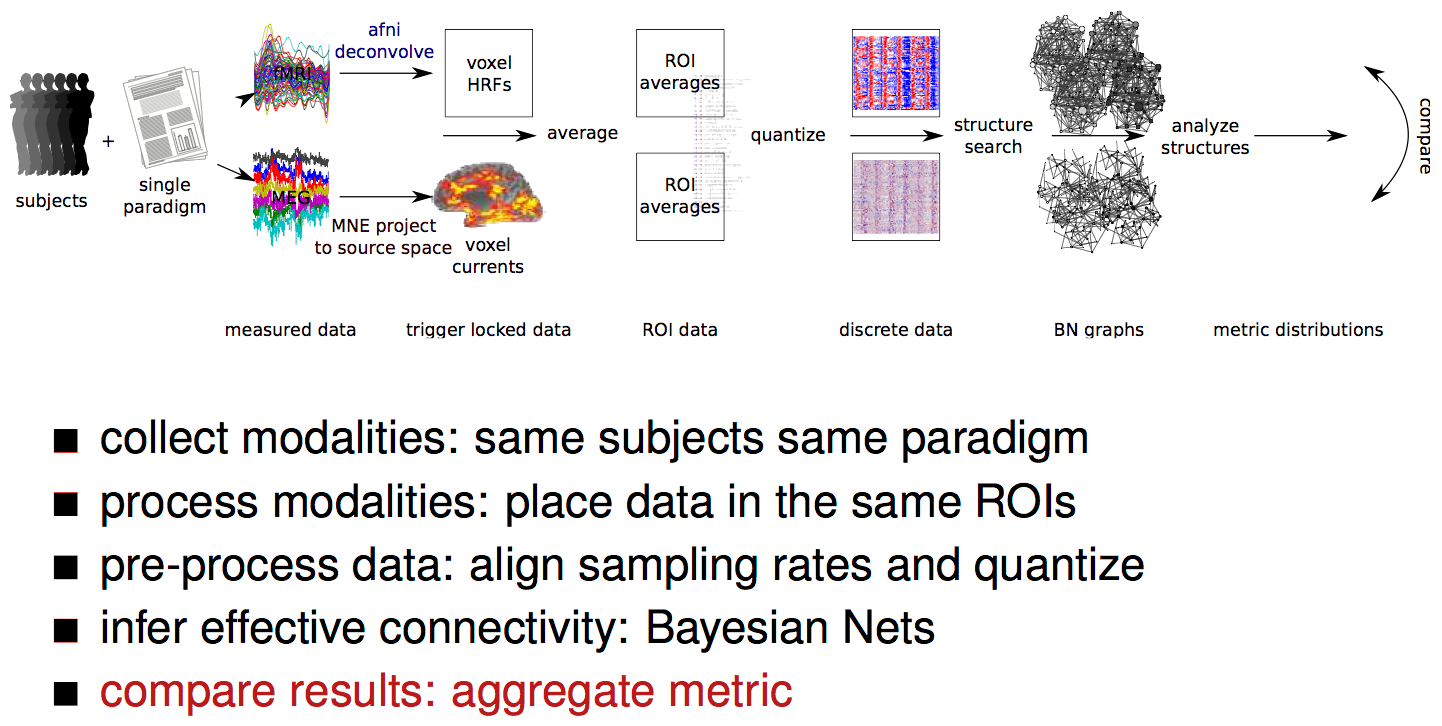
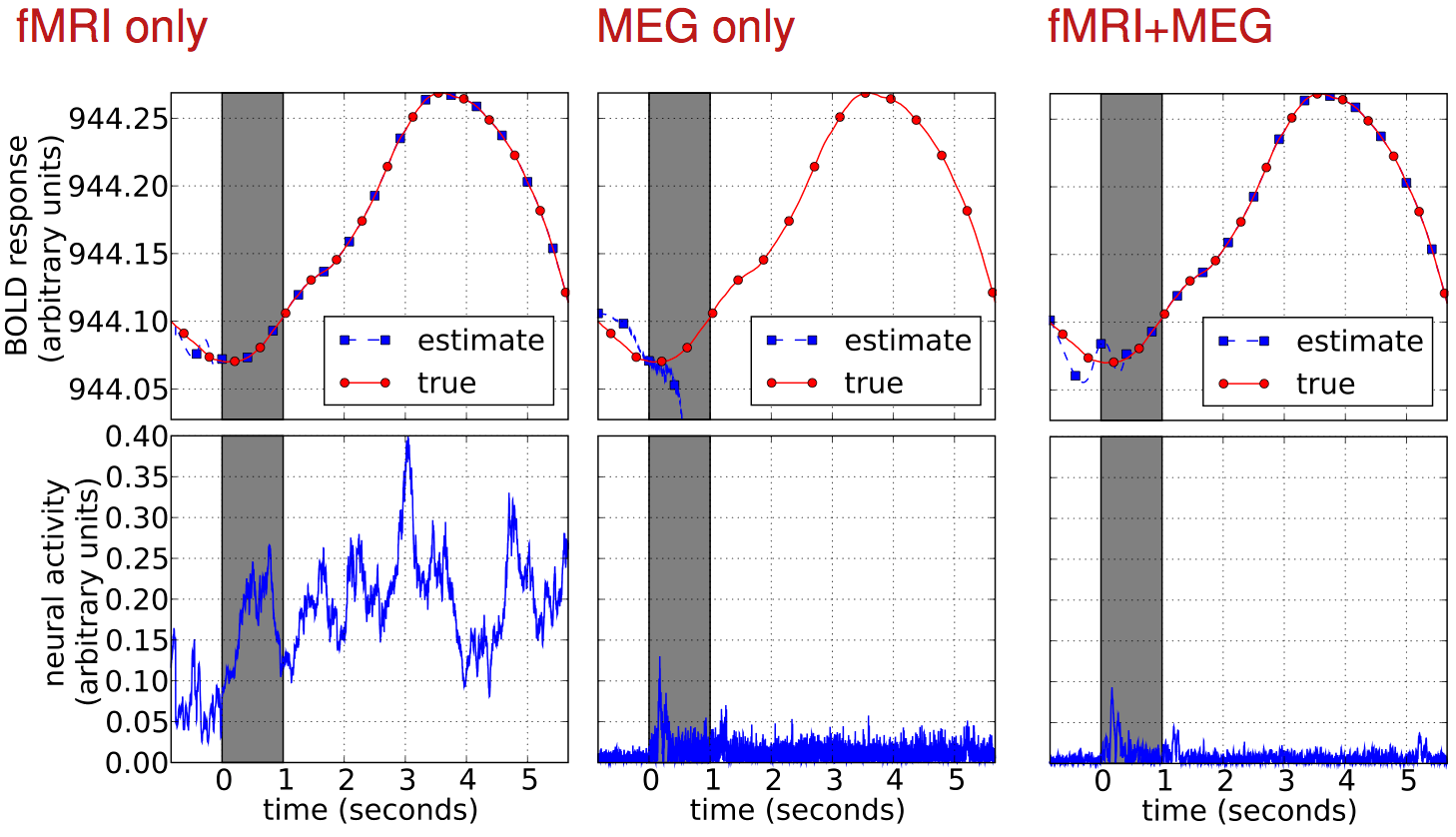
result
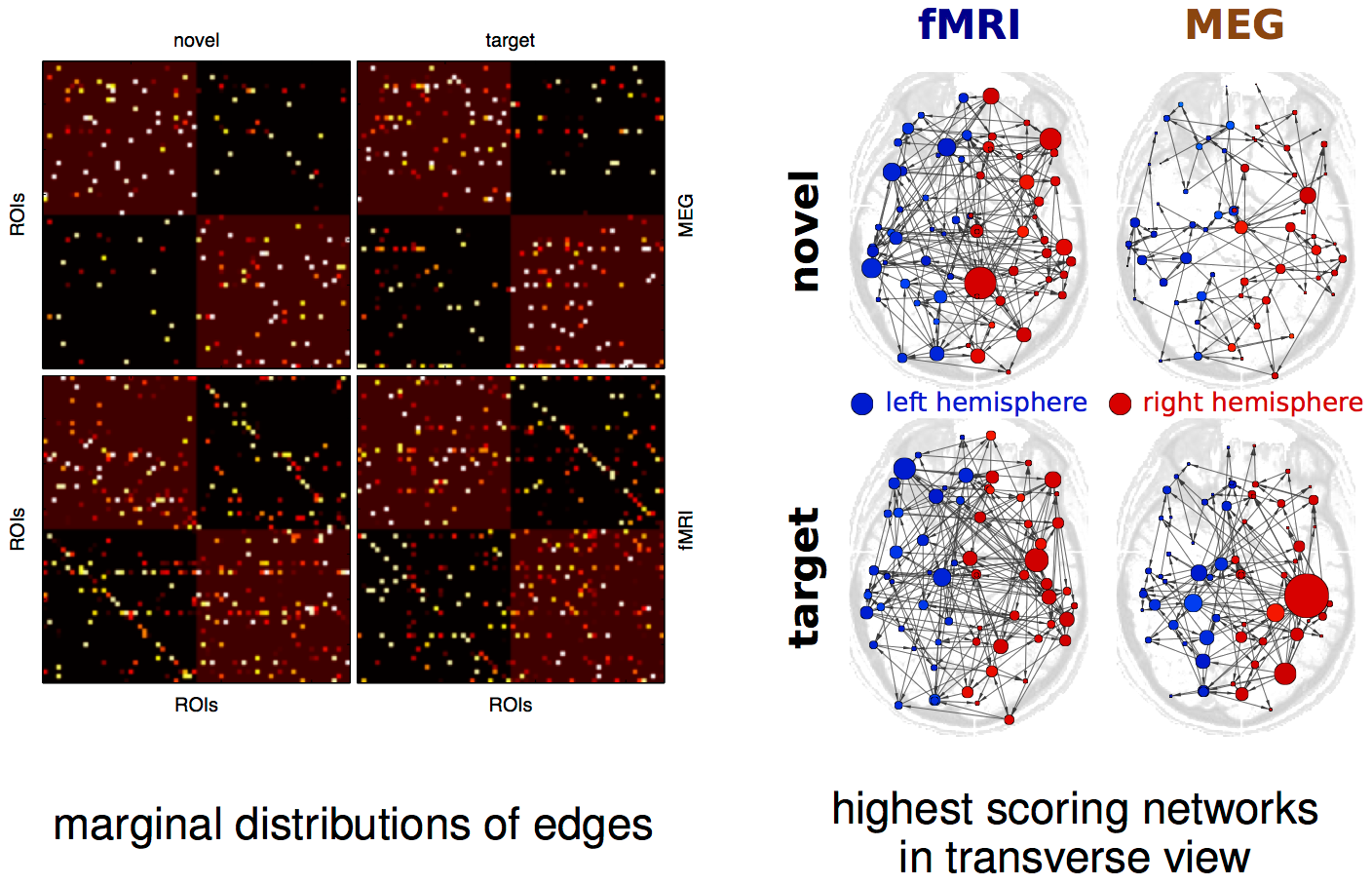
result up close
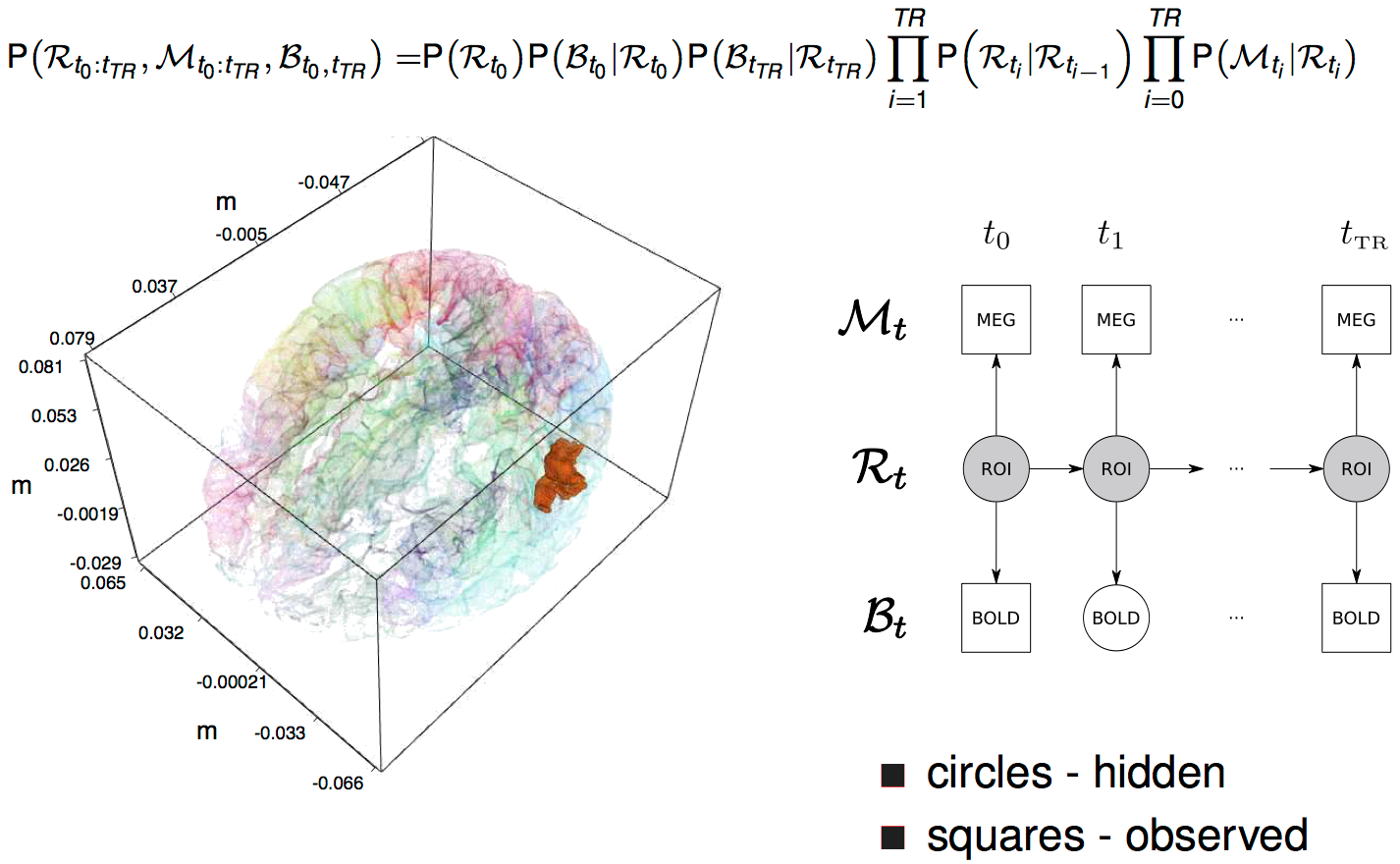
a model-based solution
dynamic Bayesian net
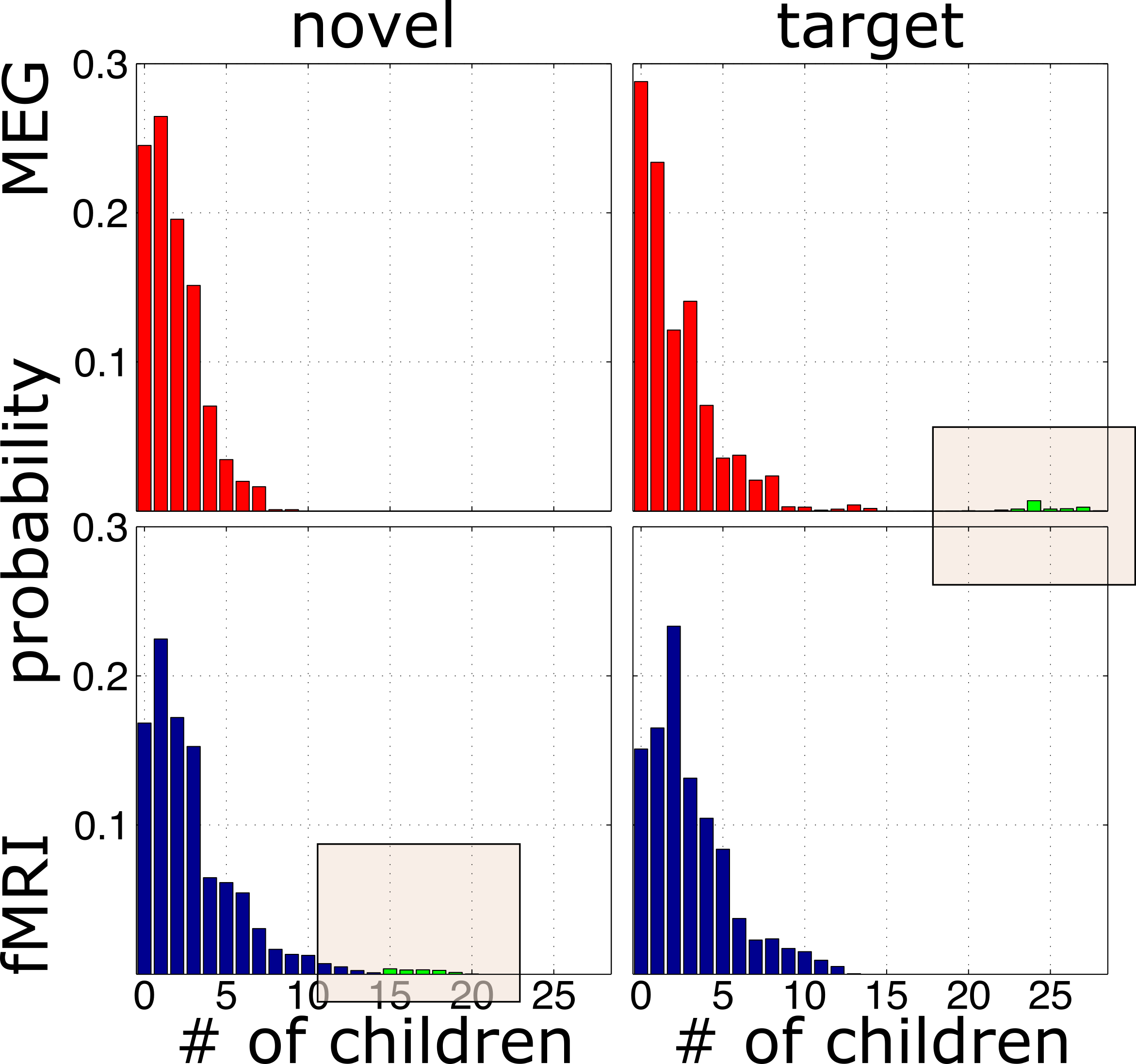
Results
dynamic Bayesian net

Causal Structure from Overlapping Variable Sets
theory
the situation
Causal timescale $\ne$ Measurement timescale
$\approx100ms$
$???$
$\approx2s$
What causal inferences can be made in this situation?
two challenges
- Forwards inference: Given a causal structure at causal timescale, what is the implied structure at (undersampled) measurement timescale?
- Backwards inference: Given inferred causal structure at measurement timescale (with unknown undersampling), what structures at causal timescale are possible?
representation
- Dynamic Bayesian Network (DBN)
- first order Markov
- causally sufficient
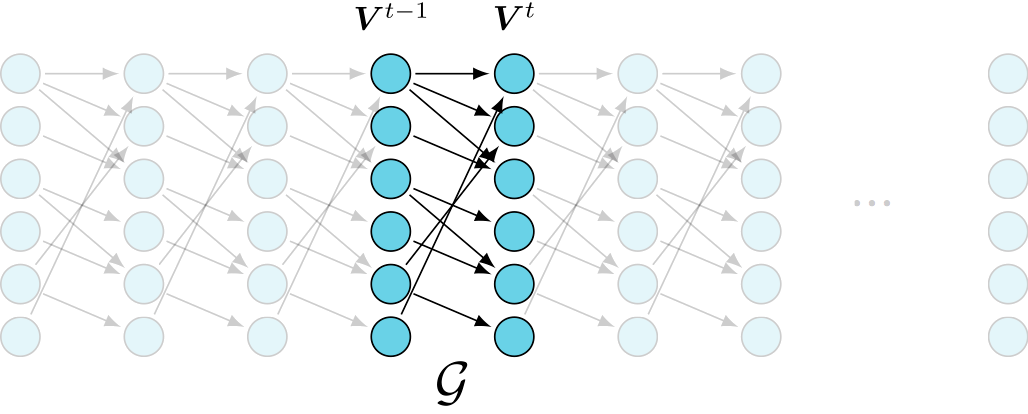
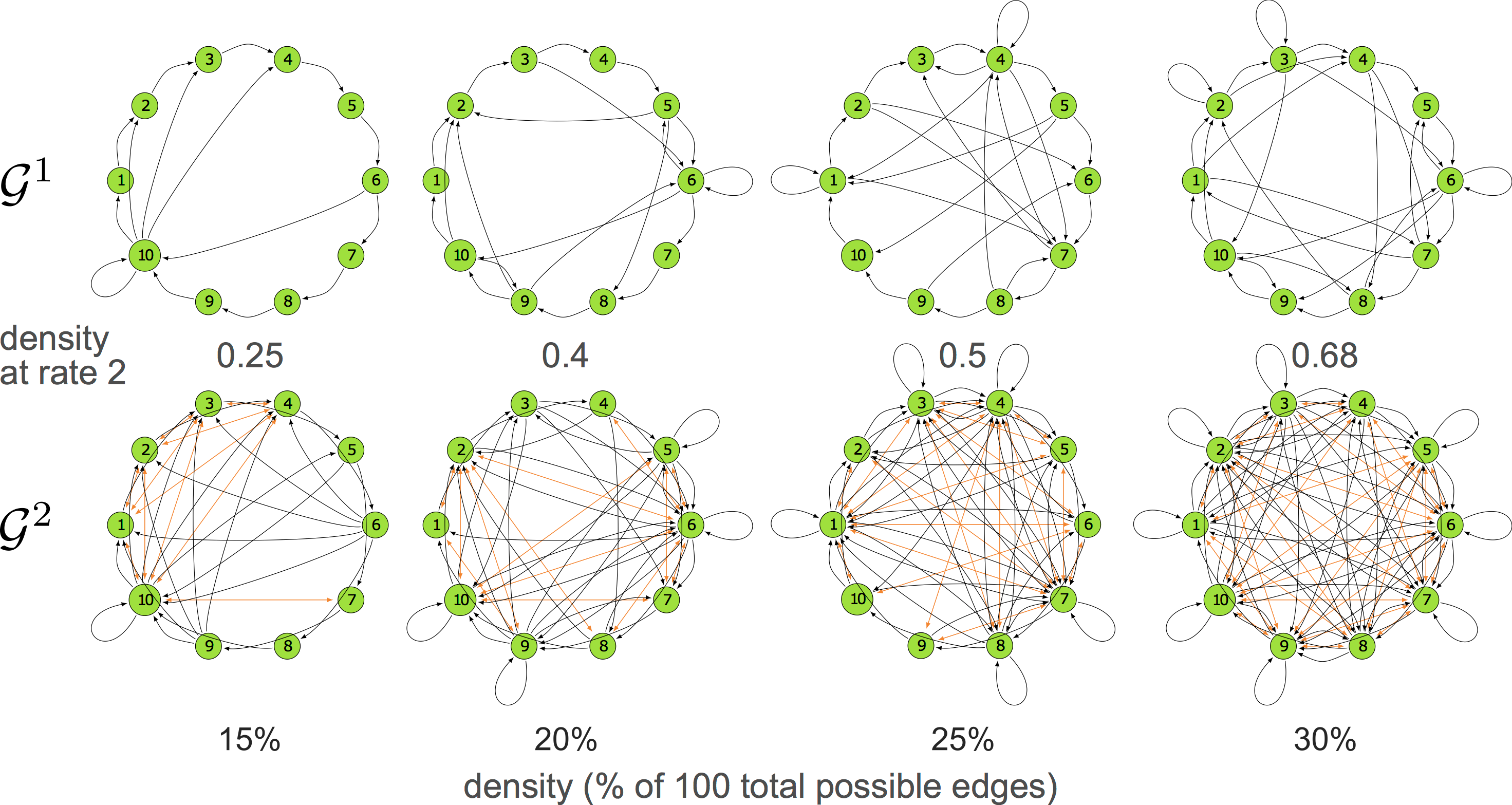
undersampling effect
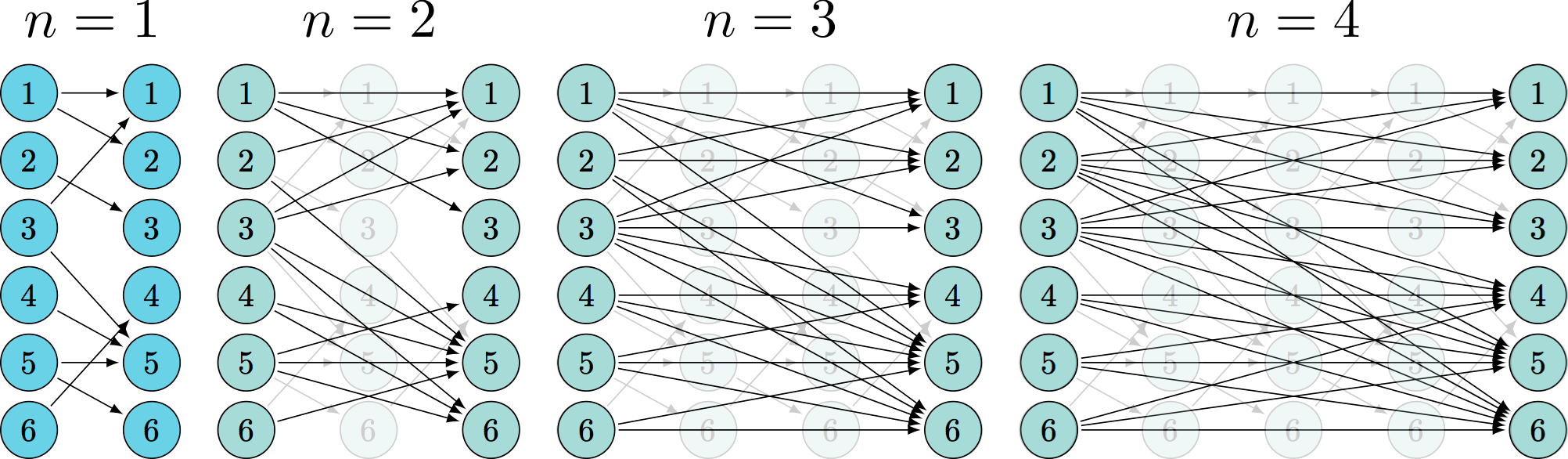
(better) representation
undersample
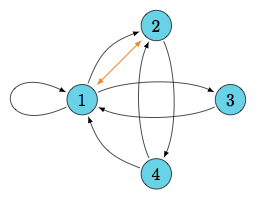
A quick look at behavior
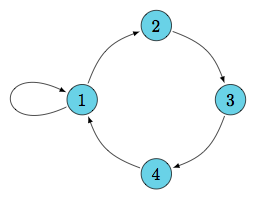
DAG

A quick look at behavior
Superclique SCC
A quick look at behavior
Oscillating SCC
algorithm
Virtual nodes
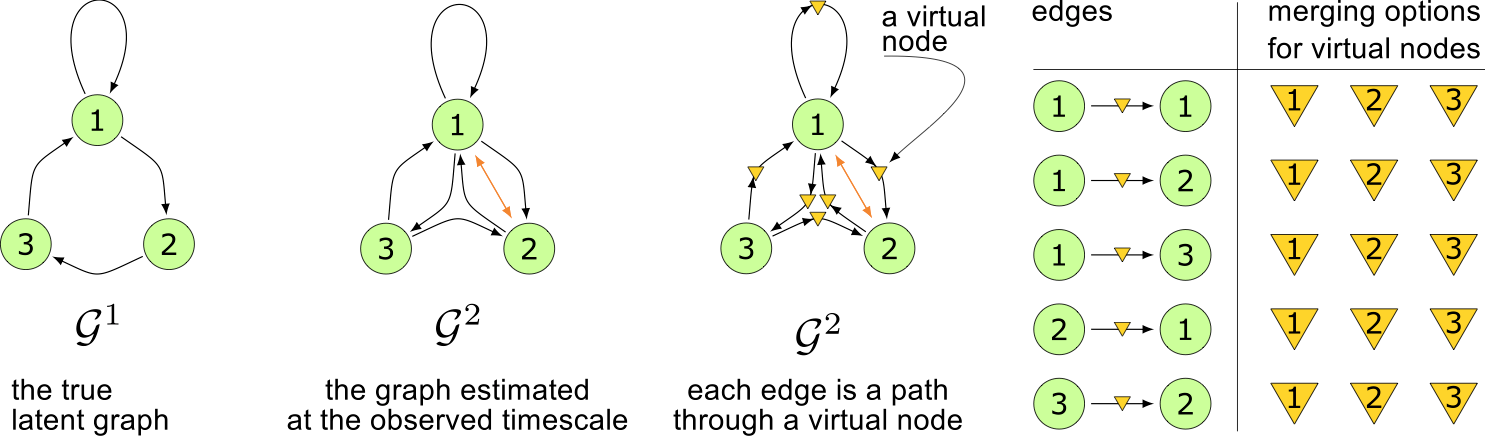
Conflict persistence
conflicts persist
${\cal{G}}^1 \text{ conflicts with } {\cal{H}}^u
\implies \forall {\cal G} \supseteq {\cal G}^1
{\cal{G}} \text{ conflicts
with } {\cal{H}}^u$
Search Tree
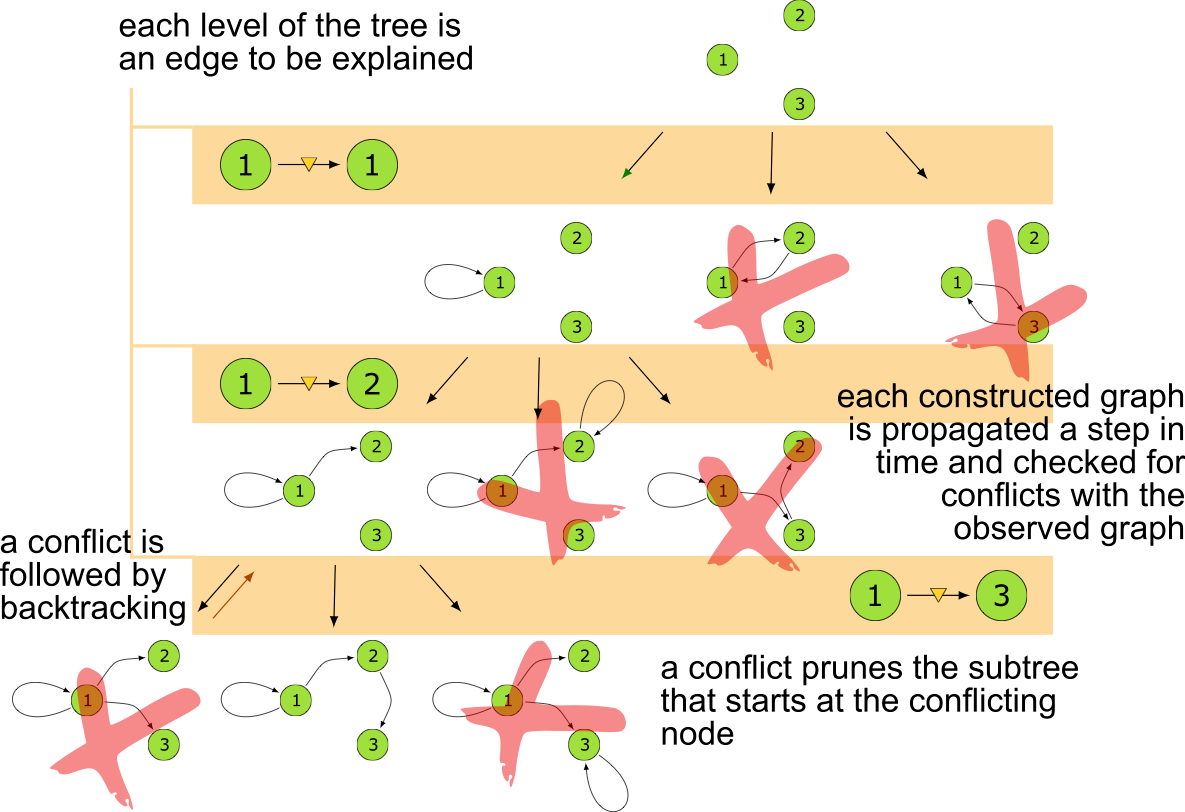
The MSL algorithm is correct and complete
Unfortunately it is slow
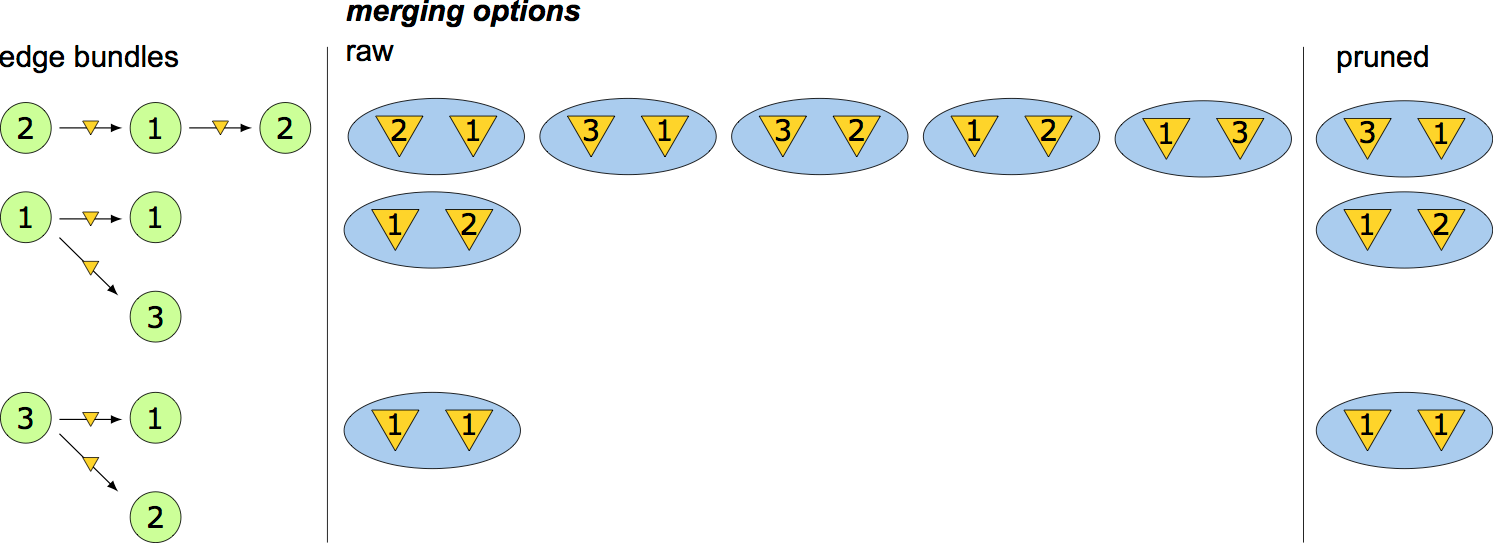
computational complexity
- $\{ m_1 , \dots , m_l \}$ - the sets of virtual node identifications for each of the edges or edge-pairs
- $\prod_i^{l} \text{len}(m_i)$ - computational complexity of using edge-pairs
- $\text{len}$ - the number of possible identifications for that particular edge or edge-pair
- Computational advantage, expressed as a log-ratio: $$ \log{r} = \sum_i^{l} \log{\text{len}(m_i)} - e\log{n}. $$
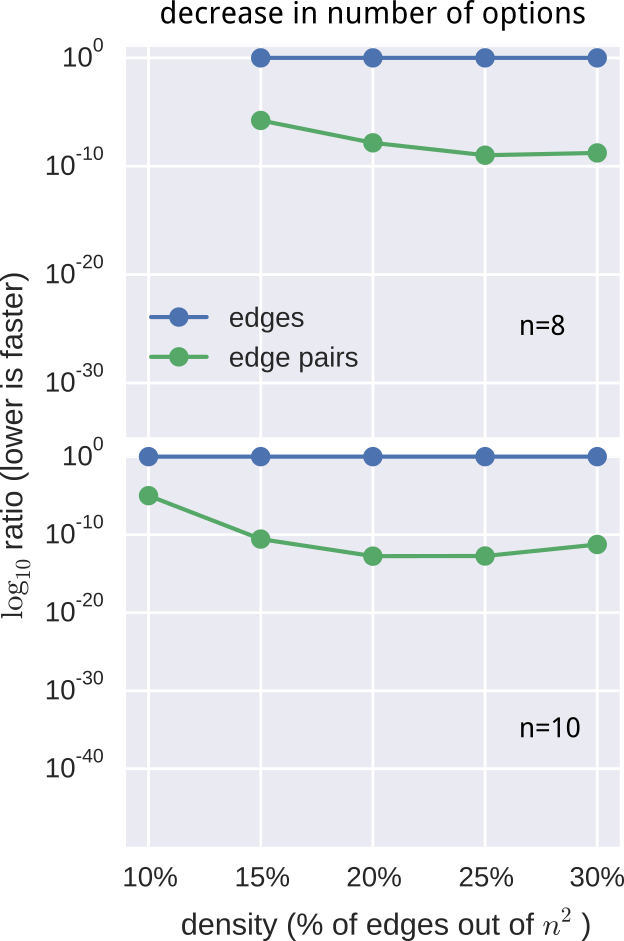
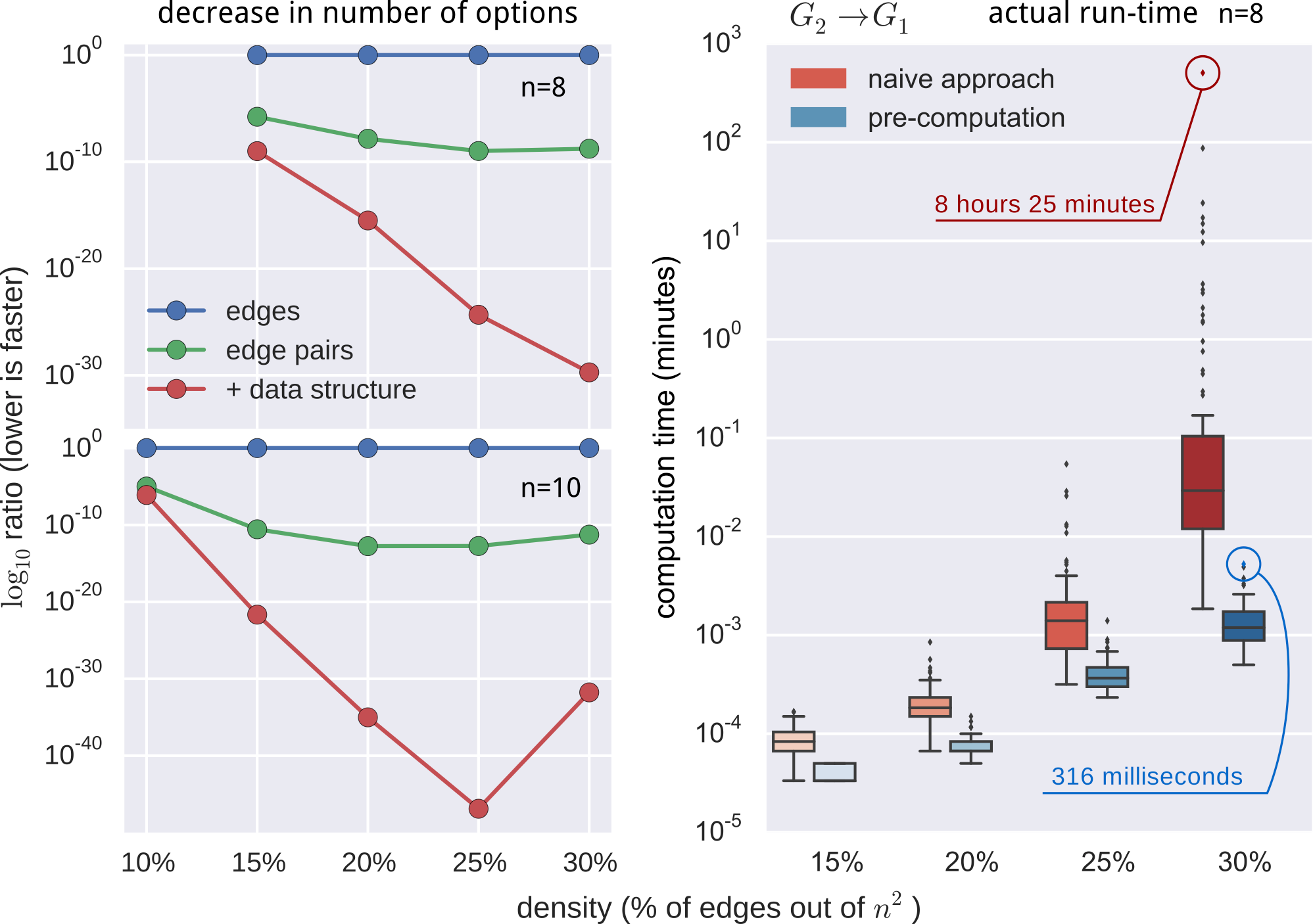
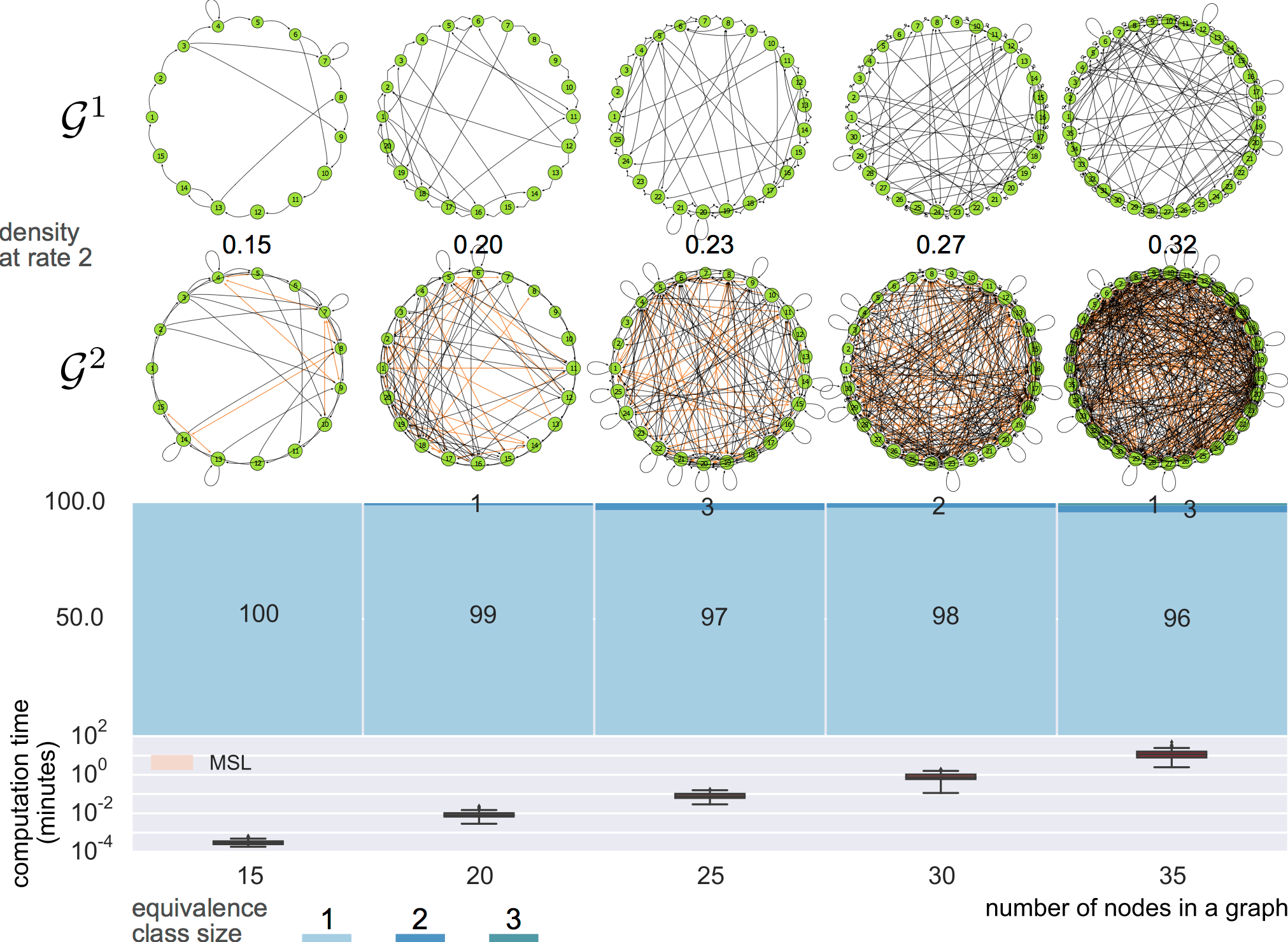
still not fast enough
- pre-computed $O(n^2)$ pruning data-structure
- employed additional constraints and observations
A virtual node $V$ in $S \xrightarrow{V} E$ cannot
be identified with node $X$ if any of the following
holds:
- $\exists W \in \chg{1}{S}\setminus X$ s.t. $\nexists W \leftrightarrow X$ in ${\cal{H}}^2$
- $\exists W\in \chg{1}{X}\setminus E$ s.t. $\nexists W \leftrightarrow E$ in ${\cal{H}}^2$
- $\exists W\in \chg{1}{X}$ s.t. $\nexists S \rightarrow W$ n ${\cal{H}}^2$
- $\exists W \in \chg{1}{E}$ s.t. $\nexists X \rightarrow W$ in ${\cal{H}}^2$
- $\exists W\in \pag{1}{S}$ s.t. $\nexists W \rightarrow X$ in ${\cal{H}}^2$
- $\exists W \in \pag{1}{X}$ s.t. $\nexists W \rightarrow E$ in ${\cal{H}}^2$
A virtual node pair $V_1, V_2$ for a fork
$E_1 \xleftarrow{V_1} S \xrightarrow{V_2} E_2$
cannot be identified with nodes $X_1, X_2$
if any of the following holds:
- $V_1$ in $E_1 \xleftarrow{V_1} S$ cannot be identified with $X_1$
- $V_2$ in $S \xrightarrow{V_2} E_2$ cannot be identified with $X_2$
- $V_1 \equiv E_2 \wedge V_2 \not\in pa_{{\cal{H}}^2}(E_1)$
- $V_2 \equiv E_1 \wedge V_1 \not\in pa_{{\cal{H}}^2}(E_2)$
- $S \equiv V_2 \wedge V_1 \ne V_2 \wedge V_1 \ne E_2$ and $\nexists E_2 \leftrightarrow V_1$ in ${\cal{H}}^2$
- $S \equiv V_1 \wedge (V_1 \equiv V_2 \vee V_2 \equiv E_2) $ and $\nexists E_1 \leftrightarrow E_2$ in ${\cal{H}}^2$
- $S \equiv V_1 \wedge (V_1 \equiv V_2 \vee V_2 \equiv E_2) $ and $\nexists E_1 \leftrightarrow E_2$ in ${\cal{H}}^2$
- $S \equiv V_2 \wedge (V_1 \equiv V_2 \vee V_1 \equiv E_1)$ and $\nexists E_1 \leftrightarrow E_2$ in ${\cal{H}}^2$
- $V_1 \equiv V_2$ and $\nexists E_1 \leftrightarrow E_2$ in ${\cal{H}}^2$
A virtual node pair $V_1, V_2$ for two-edge sequence
$S \xrightarrow{V_1} M \xrightarrow{V_2} E$
cannot be identified with $X_1, X_2$
if any of the following holds:

- $V_1$ in $S \xrightarrow{V_1} M$ cannot be merged to $X_1$
- $V_2$ in $M \xrightarrow{V_2} E$ cannot be merged to $X_2$
- $V_1 \equiv V_2 \wedge ( M \not\in pa_{{\cal{H}}^2}(M) \vee V_1 \not\in pa_{{\cal{H}}^2}(V_2) \vee S \not\in pa_{{\cal{H}}^2}(E))$

Results
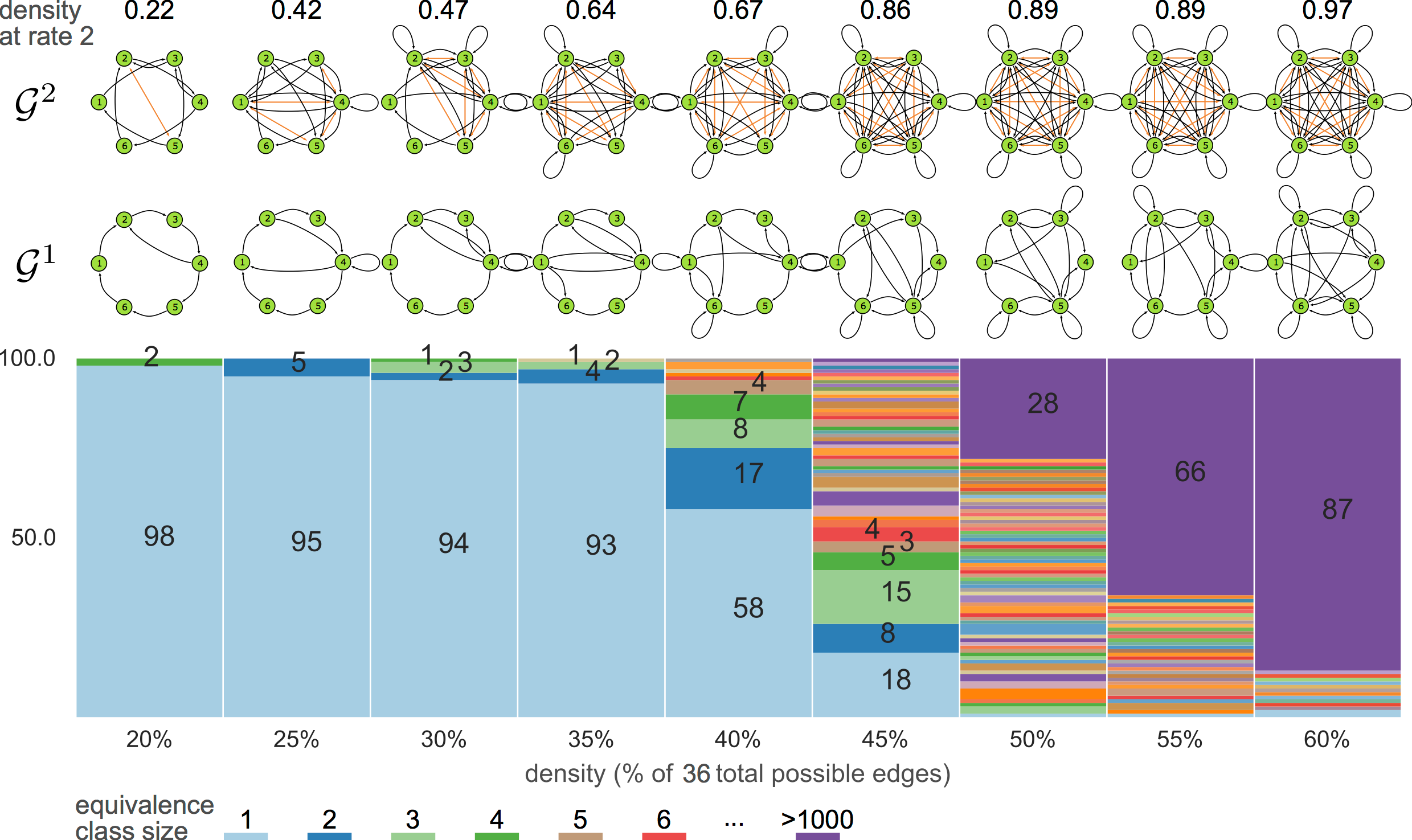
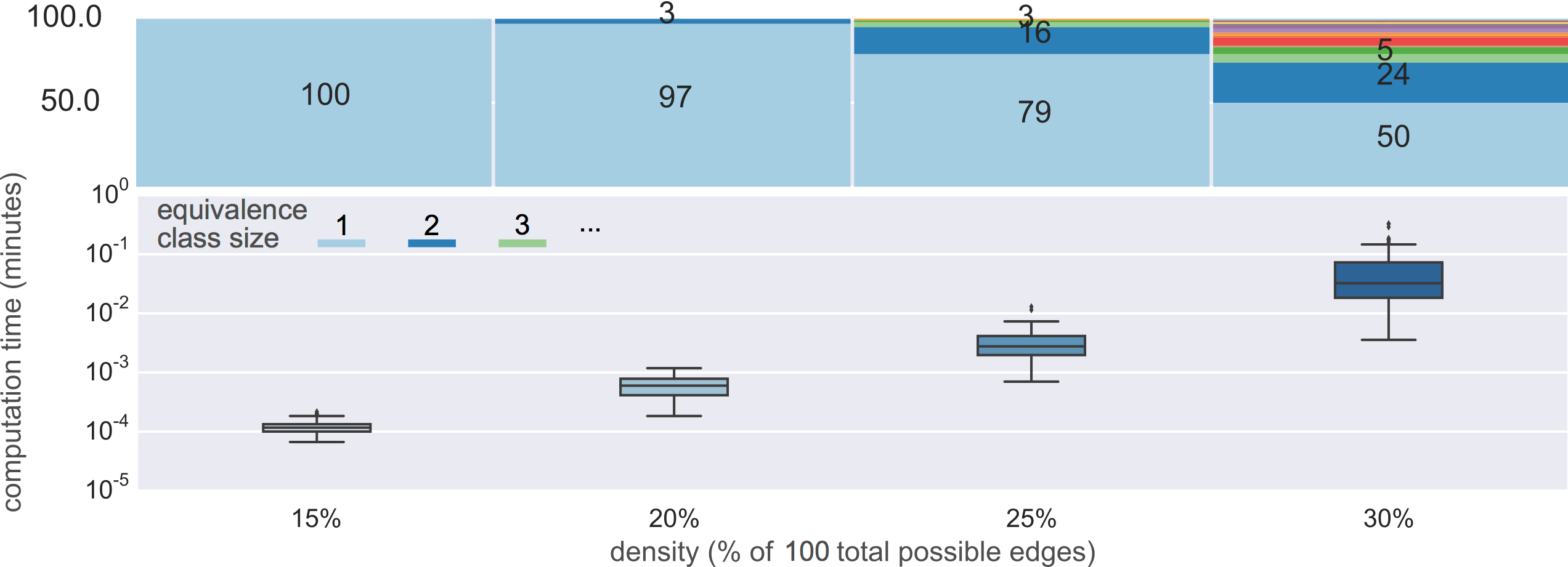
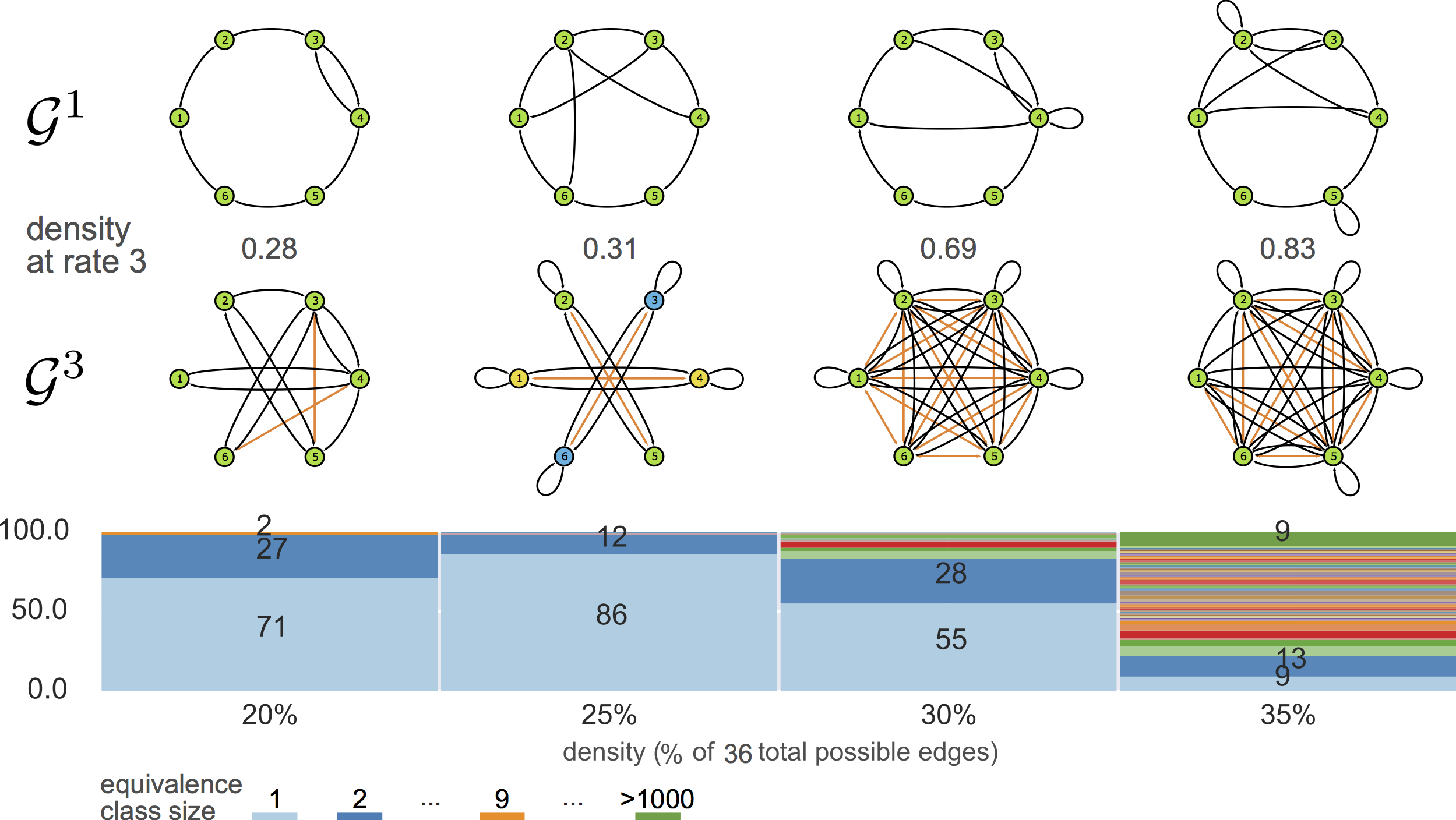
equivalence classes
6-node graphs

8-node graphs

10-node graphs


10% density

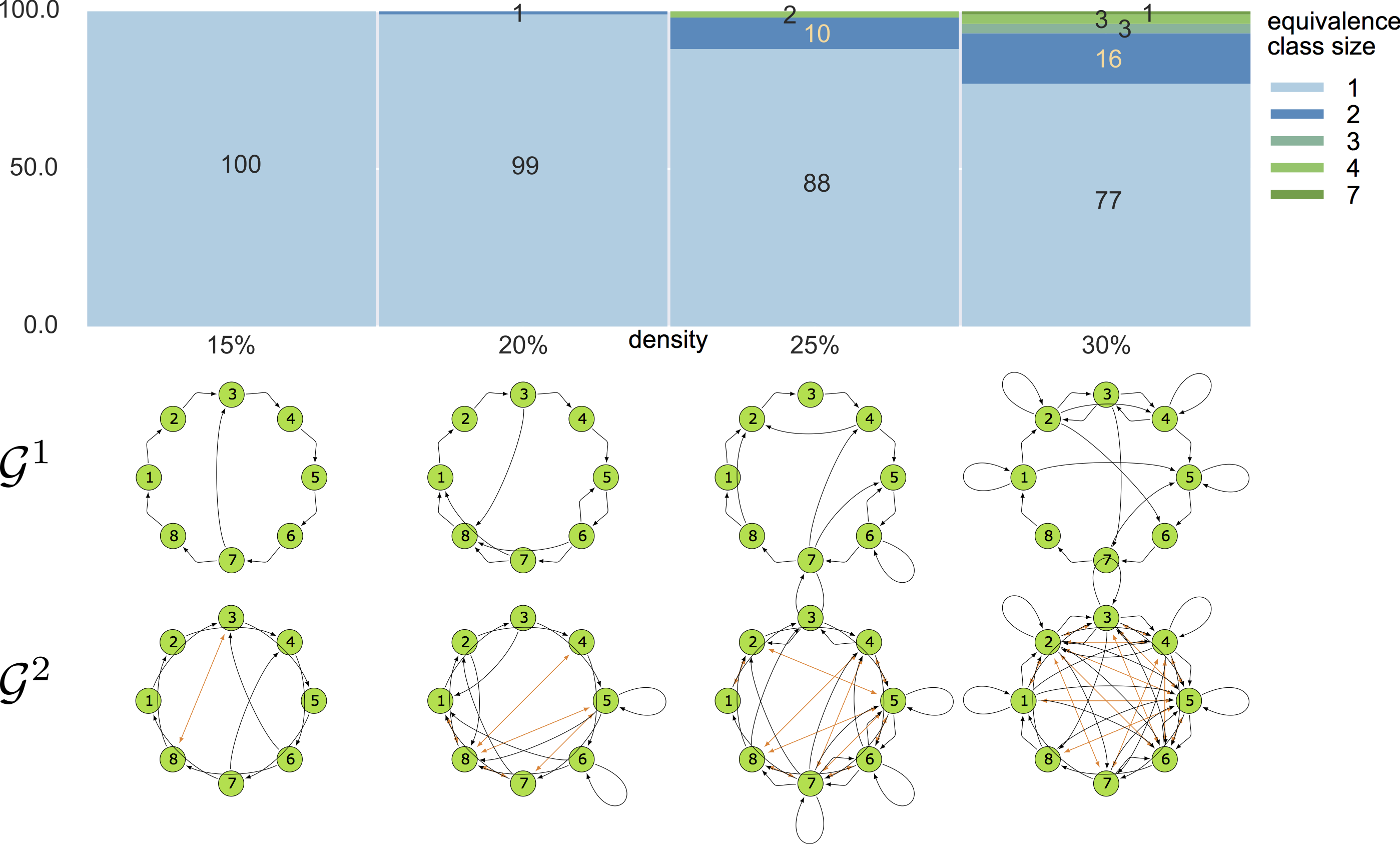
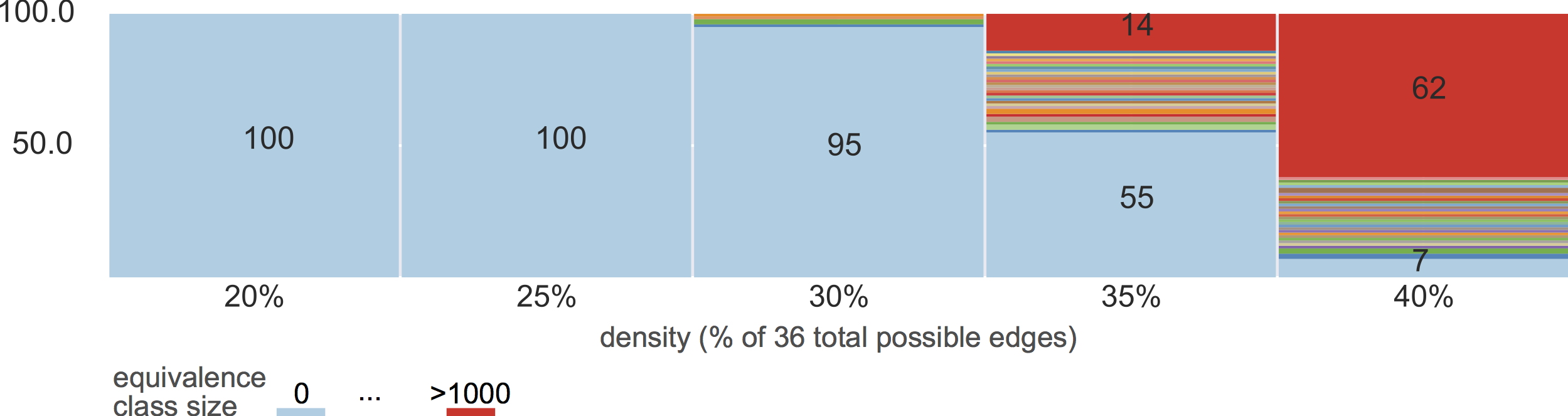
violating assumptions
feeding MSL with ${\cal G}^3$
generalizing
${\cal G}^3\rightarrow {\cal G}^1$
Results
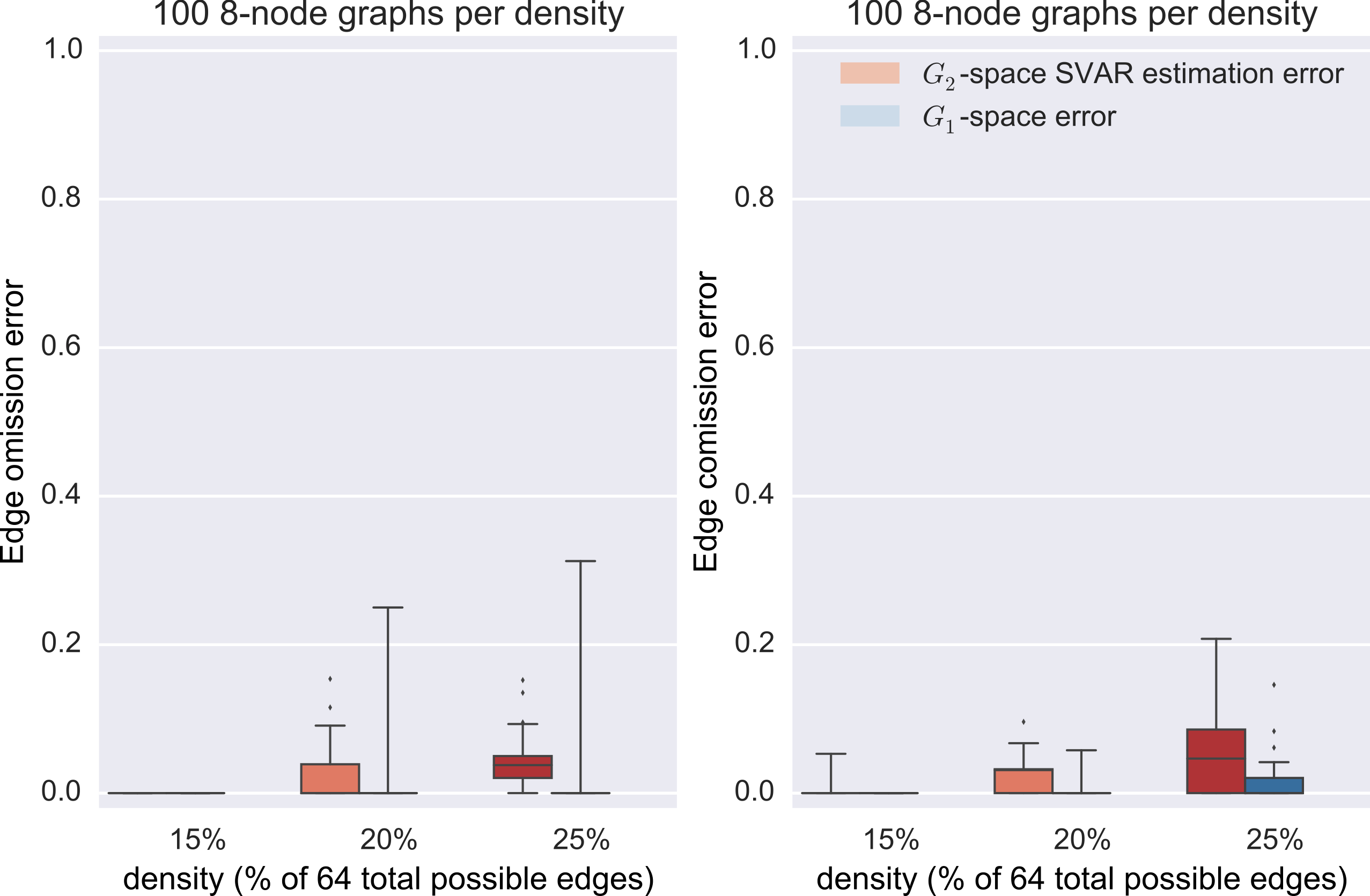
synthetic data
Data generation
- generate a random SCC graph
- convert it to a stable transition matrix
- simulate data via $\vec{x}_t = A \vec{x}_{t-1} + \vec{\eta}$
- sub-sample to rate 2
Graph estimation
- direct minimization of the negative log likelihood of the structural vector autoregressive model (SVAR) $B \vec{x}_t = A \vec{x}_{t-1} + \vec{\eta}$
discarding unreachable graphs

searching the neighborhood
Up to 5 steps away on the Hamming cube [92, 4186, 125580, 2794155, 49177128]
Conclusions
- Undersampling leads to incorrect results!
- We have solved the forward problem!
- We have solved the inverse problem!
- Equivalence classes often are singletons
- Statistical estimation errors may get help from the theory
- Our solutions are nonparametric
- MSL algorithm solves for a given undersampling rate
- Cannot solve for large high density graphs
Thank you!
research supported by NSF