.In the summer of 1939, then, Shannon arrived at one of the greatest genetics laboratories in America, and one of the greatest scientific embarrassments: the Eugenics Record Office. In 1910, when this headquarters of the American eugenics movement opened its doors, it was considered the cutting edge of progress in some circles to push for the selective breeding of the “fittest families” and the sterilization of the “defective classes.” Its founder had opined that “three or four per cent of our population is a fearful drag on our civilization,” and its longtime director even mailed state legislators custom-made estimates of the number of “defectives” in their districts. By 1939, the movement was dying, and the crimes of Nazi Germany—a regime that took eugenicists as seriously as they took themselves—were the final push into disrepute. (Chillingly enough, a Nazi poster from 1936 prominently featured the flag of the United States, along with those of other nations that had adopted eugenics laws. The inscription read: “WE DO NOT STAND ALONE.”) Somewhere on the list of Vannevar Bush’s accomplishments, then, should be his role in killing American eugenics. As president of the Carnegie Institution of Washington, which funded the Eugenics Record Office, he forced its sterilization-promoting director into retirement and ordered the office to close for good on December 31, 1939.
But the poison tree bore some useful fruit. And Shannon was there, in its last months, to collect what he could of it. Few scientists had compiled better data on heredity and inheritance than eugenicists—in some ways, eugenics are to modern genetics as alchemy is to chemistry, the disreputable relative in the attic. Perhaps the best data set of all belonged to the Eugenics Record Office, which had spent a quarter century accumulating more than one million index cards bearing information on human traits and family trees.
Many of those cards were the work of generations of field researchers; many more were volunteered by the subjects themselves, offered freely in return for advice on the fitness of their offspring. In a massive, fireproof vault the cards stood in their files row after row: traits of physiology (“biochemical deficiencies, color blindness, diabetes”), of personality (“lack of foresight, rebelliousness, trustworthiness, irritability, missile throwing, popularity, radicalness, conservativeness, nomadism”), of social behavior (“criminality, prostitution, inherited scholarship, alcoholism, patriotism, ‘traitorousness’ ”), and on and on. Each trait was coded like a book in a library. Searching for chess-playing ability would take Shannon to file 4598: 4 for mental trait, 5 for general mental ability, 9 for game-playing ability, and 8 for chess.
Mixed almost at random through this genetic Library of Babel was good, hard data; junk (unreliable testimony of untrained volunteers; exhaustive reports on circus freaks; “Midget Schedules”); and the bastard mush in between. For an example of the latter, erring on the side of junk, consider the observations of the office’s founder on “thalassophilia,” or the genetic love of the sea that allegedly causes sailing careers to be passed down through family trees: “Sometimes a father who shows no liking for the sea . . . may carry a determiner for sea-lust recessive. It is theoretically probable that some mothers are heterozygous for love of the sea, so that when married to a thalassophilic man half of their children will show sea-lust and half will not.”
While Vannevar Bush might have appreciated this line of thought, descended as he was from several generations of thalassophilic sea captains, much of the junk here lies in the simple-minded assumption that such a complex trait, if it had any basis in genetics at all, could be controlled by a single gene. But this was the murk in which the study of genetics found itself without serious math, and with still more than a decade to go until the spiral staircase of DNA first appeared under biologists’ X-rays. Pending the proof, Shannon wrote, we can only speak “as though the genes actually exist.” More to the point, without the application of statistics and probability to huge numbers of traits across entire populations, genetics would fail to account for anything more interesting than the height of pea plants or the shape of rooster combs. Eugenicists would be stuck in fruitless, and dangerous, speculations about the gene for sea-lust or for traitorousness. In Shannon’s childhood, scientists like J. B. S. Haldane, Ronald Fisher, and Sewall Wright had begun to train the big guns of statistics on biology, effecting the “great modern synthesis” between Darwinian evolution and Mendelian genetics, of which Darwin had been ignorant. It was their work that gave an unexpected value to the raw data vaulted in a selective-human-breeding warehouse, and this was why Claude Shannon was pulled out of the differential analyzer room and enlisted to continue their work in population genetics. Demand for naturalists and butterfly nets had cratered; biology, like computer building, demanded mathematicians.
Long before she helped to remake the study of genetics, Barbara Stoddard Burks, Shannon’s supervisor at Cold Spring Harbor, had narrated a children’s picture book: “Thousands of stars glittered in the heavens, and Father showed me the Southern Cross, which is made of four very bright stars in the shape of a kite. Grown people call the shape a cross, though, and some feel very proud when they have seen it because they have to travel so far before they can.”
Few scientists had traveled as far as Burks. As a child, she’d traveled with her parents, two educators, to the Philippines’ remote mountains, and when she returned to America, she starred in a picture book, Barbara’s Philippine Journey, written by her mother in young Barbara’s voice. She had traveled to the upper ranks of American science, even at a time when women were still shunted out of the allegedly purer disciplines, and from theory to fieldwork. Like Shannon, fourteen years her junior, she did her best work in her twenties; unlike him, she was a woman who had learned to cope with colleagues who stigmatized her as exceedingly aggressive for defending her conclusions with the same confidence they owned.
Burks had traveled with her field, bringing statistical rigor to the study of genetics. Much of her work was directed at the age-old nature-nurture problem, particularly with respect to intelligence. Burks’s most controversial studies were efforts to isolate the impact of genetics and environment on IQ. Nature without nurture, for instance, was a study of identical twins raised apart; nurture without nature was a comparison of the intelligence of foster children and their foster parents. At twenty-four, her study of foster children led her to the contentious conclusion that variance in IQ was 75 to 80 percent inherited. Though Burks had no truck with eugenics, the million index cards at Cold Spring Harbor brought her there for the same reason they attracted Bush’s attention, and in the eugenics office’s last years, she published a reliable method of filtering out the garbage in the files to get at the usable data.
Burks was, in other words, both an expert on and a model of intelligence; so her words carried some weight when, after reading some of his preliminary work on genetics, she wrote back to MIT that “surely Shannon is gifted—perhaps to a very high degree.” And she shared a moment of commiseration with Bush over this young man who seemed to have so little to learn from either of them: “To advise a youth like Shannon is difficult, is it not?” All the same, Shannon still had to learn the entire field of genetics from scratch. Alleles, chromosomes, heterozygosity—when he first sat down to it, he confessed to Bush, he didn’t even understand the words. From this impoverished start, he (mostly) mastered a new science and produced publishable work in less than a year.
“An Algebra for Theoretical Genetics” did, in fact, bear all the marks of a gifted novice airdropped into strange territory—for better and worse. Shannon only bothered to cite seven other studies in his bibliography, excusing himself on the grounds that his method of genetic math was literally unprecedented: “No work has been done previously along the specific algebraic lines indicated in this thesis.” But this faith in his own originality cost him: at one point, he presented as a new discovery a theorem that had been common knowledge among biologists for two decades. One class in genetics, or a few more weeks in the library, might have saved him the trouble of rediscovering it from scratch. As he confided to Bush after the fact, “Although I looked through the textbooks on Genetics fairly carefully, I didn’t have the courage to tackle the periodical literature.” At the same time, though, Shannon offered genuinely new eyes on old problems, and where his thought was original, it was almost unconsciously so. Like something of a genetic Joseph Conrad, he could reach heights of creativity in an adopted language because he had missed learning its clichés in his youth.
Shannon’s genetic algebra was, in effect, an attempt to re-create for cells what he had accomplished for circuits. Circuits before Shannon might be drawn on a blackboard, but not represented as equations. Of course, it’s much more unwieldy to manipulate a diagram than an equation, and one couldn’t even begin to use mathematical rules on a drawing. Everything in Shannon’s thesis flowed from his realization that circuits were poorly symbolized. What if genes were poorly symbolized, too? Just as Boolean algebra helped automate the mental effort of wiring machines, an algebra for genetics might help biologists predict the course of evolution. The trick, as before, was abstracting away from what was in front of his eyes. Forget the hundred switches in the box; forget that 4598 means chess playing.
“Much of the power and elegance of any mathematical theory,” Shannon wrote, “depends on use of a suitably compact and suggestive notation, which nevertheless completely describes the concepts involved.” It was a point, in fact, that was already well hammered into the heads of mathematicians, who learned early on, for instance, how Newton and Leibniz had invented the calculus almost simultaneously, but how Leibniz’s system of symbols had won out as the more intuitive. But what would be an intuitive system of symbolizing an entire population down to the genes?
As Shannon had learned in the months before sitting down to write, “genes are carried in rodlike bodies called chromosomes, a large number of genes lying side by side along the length of a chromosome.” (The chromosomes are themselves made of DNA molecules that encode genes in a four-“letter” alphabet, though no one knew that yet.) In most species more complex than a single cell, individuals have a number of pairs of chromosomes (we humans have twenty-three pairs). In species that reproduce sexually, one comes from the mother and one from the father. To simplify, Shannon suggested that we consider an organism with just two chromosome pairs and sixteen genes. He symbolized its genetic code like this:
A1 B1 C3 D5 |
E4 F1 G6 H1 |
A3 B1 C4 D3 |
E4 F2 G2 H2 |
The top left entry, A1 B1 C3 D5, is the chromosome from one parent, and the bottom left entry, A3 B1 C4 D3, is the chromosome from the other; together they make up one chromosome pair. The column of A1 and A3 (which is bolded) makes up a gene position. Taken individually, A1 is an allele, or a gene from one parent for a certain trait. A limited number of alleles is possible at any gene position, and the interaction of alleles from mother and father determines the qualities their offspring inherit. Shannon symbolized the possible alleles with the numbers in subscript. A1 and A3 are different expressions of the same trait (hair color, for instance—one for brown and one for blond), and the quality that prevails depends on which gene dominates the other.
Now simplify even further: Imagine that we want to study an entire population of individuals with respect to just two of its traits, A and B. Again, each row of symbols comes from one parent, and each column represents a gene position. Say that there are two possible alleles for A (brown hair and blond hair, for instance), and three for B (tall, medium, and short, for instance). In that case, there are twenty-one genetically distinct individuals (trust us on this), ranging from
A1B1
A1B1
to
A1B3
A2B2.
So how could we simulate that population’s genetic change over time, or predict the results if it bred at random with another group? What would the new population look like in five generations? In a thousand generations?
If we had an infinity of paper and patience, we might do the math separately for each of the twenty-one individuals, combined randomly with individuals from the crossbreeding group. That would give us one generation, and we could repeat the process over and over until we gave up. But what if the entire population and all of its relevant genes could be represented by just one algebraic expression? The expression would have to be, as Shannon said, both compact and suggestive: compact enough to use as a single variable in an equation, and suggestive enough to be “unpacked” to all of its constituent individuals whenever we wanted to halt the cycles of recombination and investigate the results.
Reasoning like that, Shannon invented a symbol to sum up an entire population: .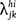
That expression is really, as he observed, “a whole group of numbers.” λ is the population as a whole. h, j, i, and k are genes. As we come to know the range of genes possible for the population, we can replace those letters with a range of numbers. The column 
is one gene position, and because the first trait under consideration has two alleles, the value of h or j can range from 1 to 2. The column 
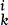is the other gene position, and because the second trait under consideration has three alleles, the value of i or k can range from 1 to 3. 
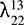now stands not for a single individual, but for a fraction of the entire population bearing the genetic code
A1 B3
A2B2.
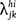is an especially elegant way of symbolizing gene frequencies, because, like any good optical illusion, it reveals two different sets of information depending on the way we read it. Read vertically, the columns of variables— and 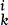—represent gene positions, which lead us to the qualities of any individual in the population. Read horizontally, the rows of variables—hi and jk—represent sets of chromosomes, each the inheritance of one parent.
This was, in other words, Shannon’s attempt to re-create the central conceptual leap of this thesis on circuits. As before, a wise choice of symbols—addition for a parallel circuit, or a grid of variables for chromosomes—would allow Shannon to simplify and simulate the future on paper. The rest of his dissertation was a set of genetic theorems that put his algebraic tools to work. He could estimate the probability that a gene would appear in an individual after n generations of mating. He could use addition to stand for the combination of several populations, and multiplication to stand for random breeding, and he showed how to calculate the product of two populations, •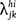 
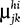. There were fractions of populations, imaginary “negative populations,” and rates of change in gene frequencies over time. He could consider “lethal factors,” or natural selection against maladaptive traits over time: evolutionary algebra. There were algebraic equations in which x was an entire group of organisms: given the genes of a known group in the present, he could work backward and identify the genes of the unknown ancestors who planted its family tree. Most important, he derived the equation—a twelve-line monster of interlocking brackets and exponents—that gave the frequencies of three different alleles in any population after any number of generations. While a number of the dissertation’s conclusions were old news, this last result, an extrapolation of the future of any three traits, was entirely new. Less than a year after learning the vocabulary, he had produced findings some five to ten years in advance of the field.
Unlike his discoveries in switching, though, Shannon’s genetic work was pitched at far too high a level of abstraction to prove useful. There is some irony in the fact that a facility built for such a practical purpose—to promote the selective breeding of humans—ended with such impractical work. In the case of all but the simplest of organisms, Shannon’s algebra demanded too much information to make real-world predictions. “My theory has to do with what happens when you have all the genetic facts,” he later explained. “But people don’t know all of them, especially for humans. They are pretty well versed on the fruitfly!” Two years after Shannon’s death, geneticists finished sequencing the human genome; yet even then, far more input on genetic variation between individual humans would have been required to render Shannon’s algebra workable. If anything was to come of Shannon’s dissertation, it would not be anything so immediately valuable as a digital computer, but rather new methods and new symbols for thinking through the problems of population genetics in the most general terms.
Even that, though, would have to materialize without Shannon’s help. He abandoned his work in genetics as soon as it was typed up and bound.
In a sense, the subject of the dissertation was Claude Shannon himself. The project had been Bush’s initiative, and the hypothesis was his. Hypothesis: the subject, a twenty-three-year-old genius, working in a scientific field in which he has no training, in which “he did not even know what the words meant,” can produce original findings in less than one year. Conclusion: confirmed, mostly.
Behind the scenes, Bush confidentially canvassed his colleagues for their opinions, admitting as he did that Shannon’s work was still marked by amateurism: “It goes on for a while and then just stops, and there are some obvious crudities.” He was prepared, then, to put the verdict to Shannon as delicately as possible. “I need your guidance before I speak to him concerning this particular thing,” he wrote to a Harvard statistician, “for what I say will either encourage or discourage him greatly.” That worry speaks to the touchy pride that Bush saw in his student, “a man who should be handled with great care”—as well as to the simple fact that Shannon’s academic life to date, from Gaylord to Cambridge, had been free of failure.
In any case, Bush was spared the work of framing bad news: the reviews came back bearing phrases like “very suitable” and “very much impressed.” Burks was even more supportive. The story went that the seventeenth-century mathematician Pascal, at the age of twelve, had independently discovered the theorems of Euclid’s geometry by drawing on his playroom floor—and Shannon’s work, Burks said, was something like that. “This, I feel strongly, should be polished a bit and then published,” Bush wrote to Shannon with some satisfaction.
For all that, Shannon ignored him: his genetics work was filed away and forgotten. There is no sign that Shannon heard any condescension in the comparison to a precocious twelve-year-old scribbling on the floor. At the same time, he seems to have had no wish to be Pascal, rediscovering common knowledge. Such discoveries might say something remarkable about their authors, an unschooled boy or an out-of-place engineer, but they said nothing new about the world. The newest element of Shannon’s dissertation was his algebraic method itself—and this would only prove worthwhile if Shannon, a young man with no clout and no network in the field, could convince geneticists to set aside their familiar tools and start using his. Shannon understood that as well as anyone: “I had a good time acting as a geneticist for a couple years,” he later joked.
Burks and Bush included, along with their praise for his work, candid assessments of its odds of making an impact. Burks wrote to MIT that “few scientists are ever able to apply creatively a new and unconventional method furnished by someone else—at least of their own generation.” Bush passed the warning on to his student, along with the praise: “I doubt very much whether your publication will result in further work by others using your method, for there are very few individuals in this general field who would be likely to do so.” The very peculiarity of Shannon’s method, the isolation in which he had invented it, would most likely consign it to irrelevance. Or, at the absolute best, it would sentence its inventor to a frustrating career as an outsider geneticist peddling his notation to skeptics. For a student who had already made his name as one of the nation’s most talented young engineers, it must have looked like an unappealing future—and an unnecessary one. Shannon, observed a later colleague, “did not need to corrupt his reputation with anything non-spectacular.”
Shannon would be adamant on the point, for any number of publications-that-might-have-been, for the rest of his life: after the effort of discovery, the effort of communication was secondary, by far. He had solved a problem to his own satisfaction—and that, as far as he was concerned, was enough, especially in the sub-spectacular cases. Shannon explained later: “After I had found the answers it was always painful to write them up or to publish them (which is how you get the acclaim).” A more magniloquent scientist might have added something about the pure Platonic joy of discovery. Not Shannon, though: “Too lazy, I guess.”
More than a half century after the dissertation was submitted to Bush and Burks, the editors of Shannon’s collected papers asked an expert in modern population genetics to read Shannon’s lost dissertation with a counterfactual eye: if it had been published, and if it had been read, would it have mattered? The reviewer compared the dissertation to the work of two other young, mathematically inclined geneticists who were also working in obscurity in the late 1930s. While he ranked Shannon as the least of the three, he admitted his regret “that the work of all three did not become widely known in 1940. It would have changed the history of the subject substantially, I think.”
Shannon would have to make his history elsewhere. The simplest explanation for his failure to publish is just that his attention did what it did so often: it wandered away. In the midst of what was supposed to be his immersion in genetics, he stopped to write a letter to his advisor:
I’ve been working on three different ideas simultaneously, and strangely enough it seems a more productive method than sticking to one problem. . . .
Off and on I have been working on an analysis of some of the fundamental properties of general systems for the transmission of intelligence, including telephony, radio, television, telegraphy, etc. . . .