The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point. Frequently the messages have meaning. . . . These semantic aspects of communication are irrelevant to the engineering problem.”
From the start, “A Mathematical Theory of Communication” demonstrated that Shannon had digested what was most incisive from the pioneers of information science. Where Nyquist used the vague concept of “intelligence” and Hartley struggled to explain the value of discarding the psychological and semantic, Shannon took it for granted that meaning could be ignored. In the same way, he readily accepted that information measures freedom of choice: what makes messages interesting is that they are “selected from a set of possible messages.” It would satisfy our intuitions, he agreed, if we stipulated that the amount of information on two punch cards doubled (rather than squared) the amount of information on one, or that two electronic channels could carry twice the information of one.
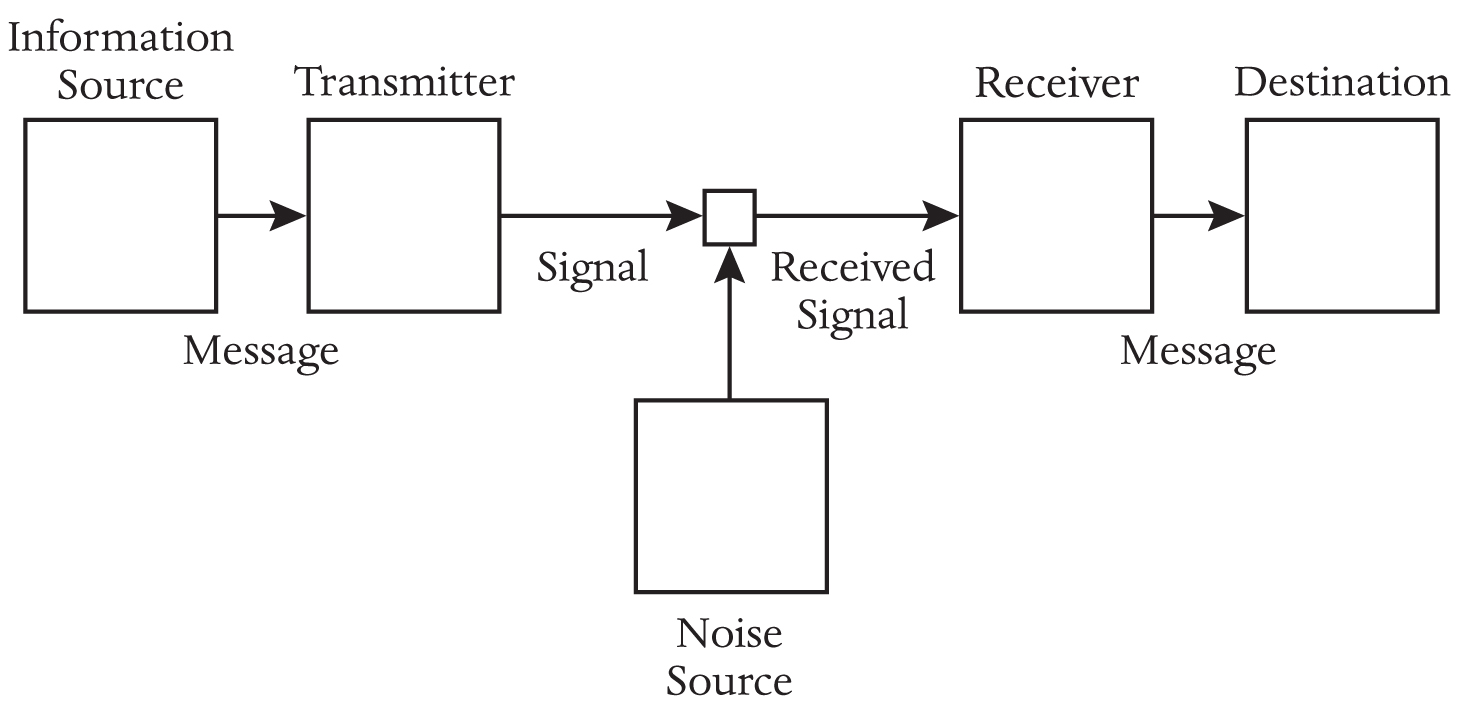
That was Shannon’s debt. What he did next demonstrated his ambition. Every system of communication—not just the ones existing in 1948, not just the ones made by human hands, but every system conceivable—could be reduced to a radically simple essence.

• The information source produces a message.
• The transmitter encodes the message into a form capable of being sent as a signal.
• The channel is the medium through which the signal passes.
• The noise source represents the distortions and corruptions that afflict the signal on its way to the receiver.
• The receiver decodes the message, reversing the action of the transmitter.
• The destination is the recipient of the message.
The beauty of this stripped-down model is that it applies universally. It is a story that messages cannot help but play out—human messages, messages in circuits, messages in the neurons, messages in the blood. You speak into a phone (source); the phone encodes the sound pressure of your voice into an electrical signal (transmitter); the signal passes into a wire (channel); a signal in a nearby wire interferes with it (noise); the signal is decoded back into sound (receiver); the sound reaches the ear at the other end (destination).
In one of your cells, a strand of your DNA contains the instructions to build a protein (source); the instructions are encoded in a strand of messenger RNA (transmitter); the messenger RNA carries the code to your cell’s sites of protein synthesis (channel); one of the “letters” in the RNA code is randomly switched in a “point mutation” (noise); each three-“letter” code is translated into an amino acid, protein’s building block (receiver); the amino acids are bound into a protein chain, and the DNA’s instructions have been carried out (destination).
It is wartime. Allied headquarters plans an assault on the enemy beaches (source); staff officers turn the plan into a written order (transmitter); copies of the order are sent to the front lines, by radio or courier or carrier pigeon (channel); headquarters has deliberately scrambled the message, encrypting it to look as random as possible (a kind of artificial “noise”); one copy reaches the Allies on the front lines, who remove the encryption with the help of a key and translate it into a battle plan, but another copy is intercepted by the enemy, whose cryptanalysts crack the code for themselves (receiver); the order issued at headquarters, and intercepted by the enemy, has turned into a strategy and counterstrategy for the battle to come (destination).
Those six boxes are flexible enough to apply even to the messages the world had not yet conceived of—messages for which Shannon was, here, preparing the way. They encompass human voices as electromagnetic waves that bounce off satellites and the ceaseless digital churn of the Internet. They pertain just as well to the codes written into DNA. Although the molecule’s discovery was still five years in the future, Shannon was arguably the first to conceive of our genes as information bearers, an imaginative leap that erased the border between mechanical, electronic, and biological messages.
Breaking down the act of communication into these universal steps enabled Shannon to home in on each step in isolation—to consider in turn what we do when we select our messages at the source, or how the struggle against noise can be fought and won in the channel. Imagining the transmitter as a distinct conceptual box proved to be especially pivotal: as we will see, the work of encoding messages for transmission turned out to hold the key to Shannon’s most revolutionary result. When we remember that Shannon’s mind was often at its best in the presence of outrageous analogies (as, earlier, between Boole’s logic and a box of switches), we can observe how this universal structure might serve as a tool for bringing promising analogies to light.
First, though, Shannon saw that information science had still failed to pin down something crucial about information: its probabilistic nature. When Nyquist and Hartley defined it as a choice from a set of symbols, they assumed that each choice from the set would be equally probable, and would be independent of all the symbols chosen previously. It’s true, Shannon countered, that some choices are like this. But only some. We could start, he later explained, by asking “what would be the simplest source you might have, or the simplest thing you were trying to send. And I’d think of tossing a coin.” A fair coin has a 50-50 chance of landing heads or tails. This simplest choice possible—heads or tails, yes or no, 1 or 0—is the most basic message that can exist. It is the kind of message that actually conforms to Hartley’s way of thinking. It would be the baseline for the true measure of information.
New sciences demand new units of measurement—as if to prove that the concepts they have been talking and talking around have at last been captured by number. The new unit of Shannon’s science was to represent this basic situation of choice. Because it was a choice of 0 or 1, it was a “binary digit.” In one of the only pieces of collaboration Shannon allowed on the entire project, he put it to a lunchroom table of his Bell Labs colleagues to come up with a snappier name. Binit and bigit were weighed and rejected, but the winning proposal was laid down by John Tukey, a Princeton professor working at Bell. Bit.
One bit is the amount of information that results from a choice between two equally likely options. So “a device with two stable positions . . . can store one bit of information.” The bit-ness of such a device—a switch with two positions, a coin with two sides, a digit with two states—lies not in the outcome of the choice, but in the number of possible choices and the odds of the choosing. Two such devices would represent four total choices and would be said to store two bits. Because Shannon’s measure was logarithmic (to base 2—in other words, the “reverse” of raising 2 to the power of a given number), the number of bits doubled each time the number of choices offered was squared:
Bits |
Choices |
1 |
2 |
2 |
4 |
4 |
16 |
8 |
256 |
16 |
65,536 |
Some choices are like this. But not all coins are fair. Not all options are equally likely. Not all messages are equally probable.
So think of the example at the opposite extreme: Think of a coin with two heads. Toss it as many times as you like—does it give you any information? Shannon insisted that it does not. It tells you nothing that you do not already know: it resolves no uncertainty.
What does information really measure? It measures the uncertainty we overcome. It measures our chances of learning something we haven’t yet learned. Or, more specifically: when one thing carries information about another—just as a meter reading tells us about a physical quantity, or a book tells us about a life—the amount of information it carries reflects the reduction in uncertainty about the object. The messages that resolve the greatest amount of uncertainty—that are picked from the widest range of symbols with the fairest odds—are the richest in information. But where there is perfect certainty, there is no information: there is nothing to be said.
“Do you swear to tell the truth, the whole truth, and nothing but the truth?” How many times in the history of courtroom oaths has the answer been anything other than “Yes”? Because only one answer is really conceivable, the answer provides us with almost no new information—we could have guessed it beforehand. That’s true of most human rituals, of all the occasions when our speech is prescribed and securely expected (“Do you take this man . . . ?”). And when we separate meaning from information, we find that some of our most meaningful utterances are also our least informative.
We might be tempted to fixate on the tiny number of instances in which the oath is denied or the bride is left at the altar. But in Shannon’s terms, the amount of information at stake lies not in one particular choice, but in the probability of learning something new with any given choice. A coin heavily weighted for heads will still occasionally come up tails—but because the coin is so predictable on average, it’s also information-poor.
Still, the most interesting cases lie between the two extremes of utter uncertainty and utter predictability: in the broad realm of weighted coins. Nearly every message sent and received in the real world is a weighted coin, and the amount of information at stake varies with the weighting. Here, Shannon showed the amount of information at stake in a coin flip in which the probability of a given side (call it p) varies from 0 percent to 50 percent to 100 percent:
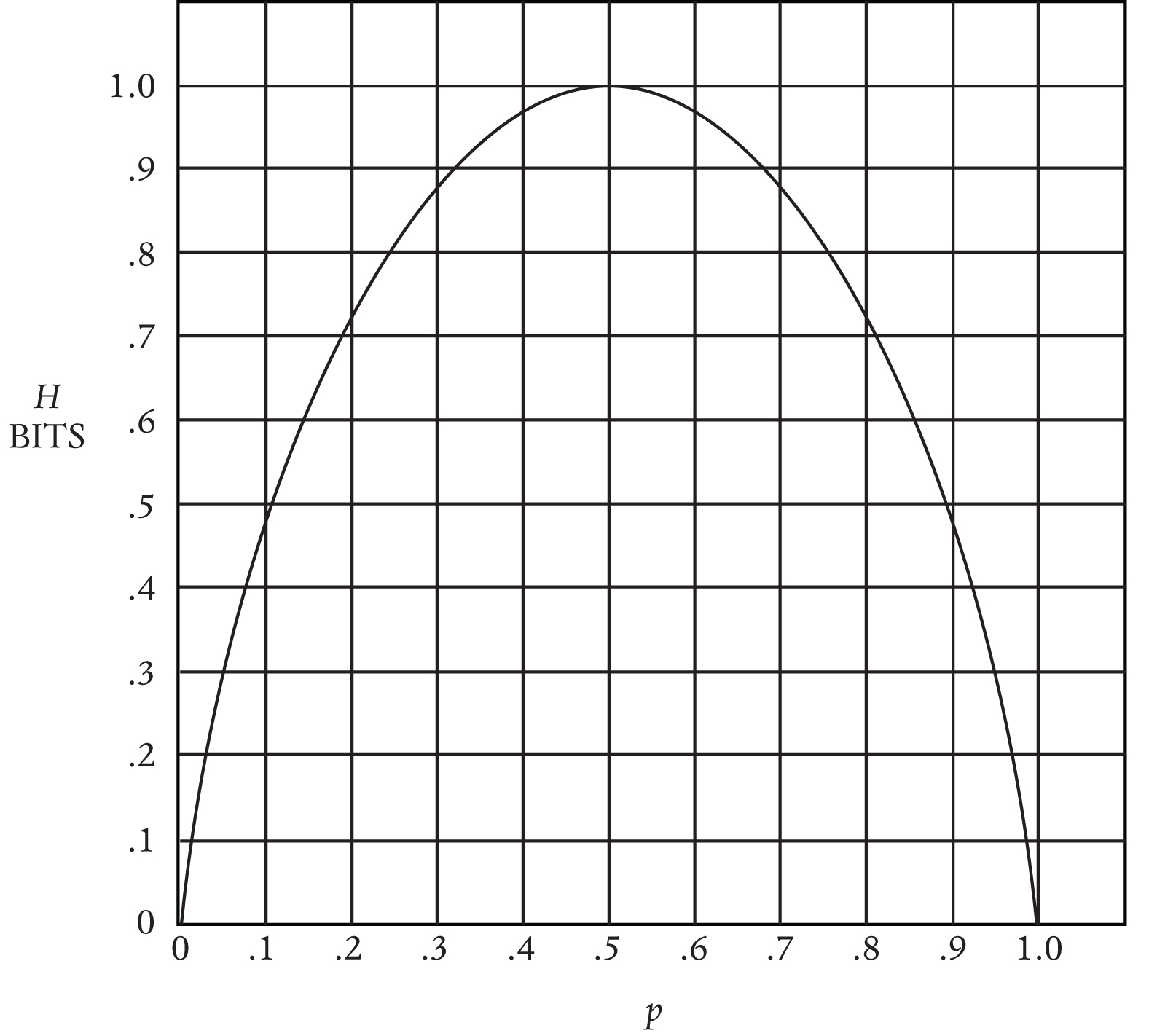
The case of 50-50 odds offers a maximum of one bit, but the amount of surprise falls off steadily as the choice grows more predictable in either direction, until we reach the perfectly predictable choice that tells us nothing. The special 50-50 case was still described by Hartley’s law. But now it was clear that Hartley’s theory was consumed by Shannon’s: Shannon’s worked for every set of odds. In the end, the real measure of information depended on those odds:
H = -p log p – q log q
Here, p and q are the probabilities of the two outcomes—of either face of the coin, or of either symbol that can be sent—which together add up to 100 percent. (When more than two symbols are possible, we can insert more probabilities into the equation.) The number of bits in a message (H) hangs on its uncertainty: the closer the odds are to equal, the more uncertain we are at the outset, and the more the result surprises us. And as we fall away from equality, the amount of uncertainty to be resolved falls with it. So think of H as a measure of the coin’s “average surprise.” Run the numbers for a coin weighted to come up heads 70 percent of the time and you find that flipping it conveys a message worth just about .9 bits.
Now, the goal of all this was not merely to grind out the precise number of bits in every conceivable message: in situations more complicated than a coin flip, the possibilities multiply and the precise odds of each become much harder to pin down. Shannon’s point was to force his colleagues to think about information in terms of probability and uncertainty. It was a break with the tradition of Nyquist and Hartley that helped to set the rest of Shannon’s project in motion—though, true to form, he dismissed it as trivial: “I don’t regard it as so difficult.”
Difficult or not, it was new, and it revealed new possibilities for transmitting information and conquering noise. We can turn unfair odds to our favor.
For the vast bulk of messages, in fact, symbols do not behave like fair coins. The symbol that is sent now depends, in important and predictable ways, on the symbol that was just sent: one symbol has a “pull” on the next. Take an image: Hartley showed how to measure its information content by gauging the intensity of each “elementary area.” But in images that resemble anything other than TV static, intensities are not splattered randomly across the pixels: each pixel has pull. A light pixel is more likely to appear next to a light pixel, a dark next to a dark. Or, suggested Shannon, think of the simplest case of telegraph messages. (By now it was common to appeal to the telegraph as the most basic model of discrete communication, fit for simplification and study; even as the telegraph grew obsolete, it continued to live a productive afterlife in information theory papers.) Reduce the alphabet to three basic Morse characters of dot, dash, and space. Whatever the message, a dot can be followed by a dot, dash, or space; a dash can be followed by a dot, dash, or space—but a space can only be followed by a dot or dash. A space is never supposed to be followed by another space. The choice of symbols is not perfectly free. True, a random machine in charge of a telegraph key might break the rules and ignorantly send a space after a space—but nearly all the messages that interest engineers do come with implicit rules, are something less than free, and Shannon taught engineers how to take huge advantage of this fact.
This was the hunch that Shannon had suggested to Hermann Weyl in Princeton in 1939, and which he had spent almost a decade building into theory: Information is stochastic. It is neither fully unpredictable nor fully determined. It unspools in roughly guessable ways. That’s why the classic model of a stochastic process is a drunk man stumbling down the street. He doesn’t walk in the respectably straight line that would allow us to predict his course perfectly. Each lurch looks like a crapshoot. But watch him for long enough and we’ll see patterns start to emerge from his stumble, patterns that we could work out statistically if we cared to. Over time, we’ll develop a decent estimation of the spots on the pavement on which he’s most likely to end up; our estimates are even more likely to hold if we begin with some assumptions about the general walking behavior of drunks. For instance, they tend to gravitate toward lampposts.
Remarkably, as Shannon showed, this model also describes the behavior of messages and languages. Whenever we communicate, rules everywhere restrict our freedom to choose the next letter and the next pineapple.I Because these rules render certain patterns more likely and certain patterns almost impossible, languages like English come well short of complete uncertainty and maximal information: the sequence “th” has already occurred 6,431 times in this book, the sequence “tk” just this once. From the perspective of the information theorist, our languages are hugely predictable—almost boring.
To prove it, Shannon set up an ingenious, if informal, experiment in garbled text: he showed how, by playing with stochastic processes, we can construct something resembling the English language from scratch. Shannon began with complete randomness. He opened a book of random numbers, put his finger on one of the entries, and wrote down the corresponding character from a 27-symbol “alphabet” (26 letters, plus a space). He called it “zero-order approximation.” Here’s what happened:
XFOML RXKHRJFFJUJ ZLPWCFWKCYJ FFJEYVKCQSGHYD QPAAMKBZAACIBZLHJQD.
There are equal odds for each character, and no character exerts a “pull” on any other. This is the printed equivalent of static. This is what our language would look like if it were perfectly uncertain and thus perfectly informative.
But we do have some certainty about English. For one, we know that some letters are likelier than others. A century before Shannon, Samuel Morse (inspired by some experimental rifling through a typesetter’s box of iron characters) had built his hunches about letter frequency into his telegraph code, assigning “E” an easy single dot and “Q” a more cumbersome dash-dash-dot-dash. Morse got it roughly right: by Shannon’s time, it was known that about 12 percent of English text is the letter “E,” and just 1 percent the letter “Q.” With a table of letter frequencies in one hand and his book of random numbers in the other, Shannon restacked the odds for each character. This is “first-order approximation”:
OCRO HLI RGWR NMIELWIS EU LL NBNESEBYA TH EEI ALHENHTTPA OOBTTVA NAH BRL.
More than that, though, we know that our freedom to insert any letter into a line of English text is also constrained by the character that’s just come before. “K” is common after “C,” but almost impossible after “T.” A “Q” demands a “U.” Shannon had tables of these two-letter “digram” frequencies, but rather than repeat the cumbersome process, he took a cruder tack, confident that his point was still made. To construct a text with reasonable digram frequencies, “one opens a book at random and selects a letter at random on the page. This letter is recorded. The book is then opened to another page and one reads until this letter is encountered. The succeeding letter is then recorded. Turning to another page this second letter is searched for and the succeeding letter is recorded, etc.” If all goes well, the text that results reflects the odds with which one character follows another in English. This is “second-order approximation”:
ON IE ANTSOUTINYS ARE T INCTORE ST BE S DEAMY ACHIN D ILONASIVE TUCOOWE AT TEASONARE FUSO TIZIN ANDY TOBE SEACE CTISBE.
Out of nothing, a stochastic process has blindly created five English words (six, if we charitably supply an apostrophe and count ACHIN’). “Third-order approximation,” using the same method to search for trigrams, brings us even closer to passable English:
IN NO IST LAT WHEY CRATICT FROURE BIRS GROCID PONDENOME OF DEMONSTURES OF THE REPTAGIN IS REGOACTIONA OF CRE.
Not only are two- and three-letter combinations of letters more likely to occur together, but so are entire strings of letters—in other words, words. Here is “first-order word approximation,” using the frequencies of whole words:
REPRESENTING AND SPEEDILY IS AN GOOD APT OR COME CAN DIFFERENT NATURAL HERE HE THE A IN CAME THE TO OF TO EXPERT GRAY COME TO FURNISHES THE LINE MESSAGE HAD BE THESE.
Even further, our choice of the next word is strongly governed by the word that has just gone before. Finally, then, Shannon turned to “second-order word approximation,” choosing a random word, flipping forward in his book until he found another instance, and then recording the word that appeared next:
THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED.
“The particular sequence of ten words ‘attack on an English writer that the character of this’ is not at all unreasonable,” Shannon observed with pride.II
From gibberish to reasonable, the passages grew closer and closer to passable text. They were not written, but generated: the only human intervention came in manipulating the rules. How, Shannon asked, do we get to English? We do it by making our rules more restrictive. We do it by making ourselves more predictable. We do it by becoming less informative. And these stochastic processes are just a model of the unthinking choices we make whenever we speak a sentence, whenever we send any message at all.
It turns out that some of the most childish questions about the world—“Why don’t apples fall upwards?”—are also the most scientifically productive. If there is a pantheon of such absurd and revealing questions, it ought to include a space for Shannon’s: “Why doesn’t anyone say XFOML RXKHRJFFJUJ?” Investigating that question made clear that our “freedom of speech” is mostly an illusion: it comes from an impoverished understanding of freedom. Freer communicators than us—free, of course, in the sense of uncertainty and information—would say XFOML RXKHRJFFJUJ. But in reality, the vast bulk of possible messages have already been eliminated for us before we utter a word or write a line. Or, to alter just slightly one of the fortuitous sequences that emerged by chance on Shannon’s notepad: THE LINE MESSAGE HAD [TO] BE THESE.
Still, who cares about letter frequencies?
For one, cryptanalysts do—and Shannon was one of the best. He was familiar with the charts of letter and digram and trigram frequencies because they were the codebreaker’s essential tool kit. In nearly any code, certain symbols will predominate, and these symbols are likely to stand for the most common characters. Recall how, in Shannon’s favorite childhood story, “The Gold-Bug,” the eccentric Mr. Legrand uncovered a buried treasure by cracking this seemingly impenetrable block of code:
53‡‡†305))6*;4826)4‡.)4‡);806*;48†8’60))85;]8*:‡*8†83
(88)5*†;46(;88*96*?;8)*‡(;485);5*†2:*‡(;4956*2(5*-4)8’8*; 4069285);)6†8)4‡‡;1(‡9;48081;8:8‡1;48†85;4)485†528806*81
(‡9;48;(88;4(‡?34;48)4‡;161;:188;‡?;
He began, as all good codebreakers did, by counting frequencies. The symbol “8” occurred more than any other, 33 times. This small fact was the crack that brought the entire structure down. Here, in words that captivated Shannon as a boy, is how Mr. Legrand explained it:
Now, in English, the letter which most frequently occurs is e . . . An individual sentence of any length is rarely seen, in which it is not the prevailing character. . . .
As our predominant character is 8, we will commence by assuming it as the e of the natural alphabet. . . .
Now, of all words in the language, “the” is the most usual; let us see, therefore, whether they are not repetitions of any three characters in the same order of collocation, the last of them being 8. If we discover repetitions of such letters, so arranged, they will most probably represent the word “the.” On inspection, we find no less than seven such arrangements, the characters being ;48. We may, therefore, assume that the semicolon represents t, that 4 represents h, and that 8 represents e—the last being now well confirmed. Thus a great step has been taken.
Being the work of a semiliterate pirate, the code was easy enough to break. More sophisticated ciphers would employ any number of stratagems to foil frequency counts: switching code alphabets partway through a message, eliminating double vowels and double consonants, simply doing without the letter “e.” The codes that Shannon tested for Roosevelt and that Turing cracked for Churchill were more convoluted still. But in the end, codebreaking remained possible, and remains so, because every message runs up against a basic reality of human communication. It always involves redundancy; to communicate is to make oneself predictable.
This was the age-old codebreaker’s intuition that Shannon formalized in his work on information theory: codebreaking works because our messages are less, much less, than fully uncertain. To be sure, it was not that Shannon’s work in cryptography drove his breakthrough in information theory: he began thinking about information years before he began thinking about codes in any formal sense—before, in fact, he knew that he’d be spending several years as a cryptographer in the service of the American government. At the same time, his work on information and his work on codes grew from a single source: his interest in the unexamined statistical nature of messages, and his intuition that a mastery of this nature might extend our powers of communication. He would explain later, “I wrote [the information theory paper], which in a sense sort of justified some of the time I’d been putting into [cryptography], at least in my mind. . . . But there was this close connection. I mean they are very similar things. . . . Information, at one time trying to conceal it, and at the other time trying to transmit it.”
In Shannon’s terms, the feature of messages that makes code-cracking possible is redundancy. A historian of cryptography, David Kahn, explained it like this: “Roughly, redundancy means that more symbols are transmitted in a message than are actually needed to bear the information.” Information resolves our uncertainty; redundancy is every part of a message that tells us nothing new. Whenever we can guess what comes next, we’re in the presence of redundancy. Letters can be redundant: because Q is followed almost automatically by U, the U tells us almost nothing in its own right. We can usually discard it, and many more letters besides. As Shannon put it, “MST PPL HV LTTL DFFCLTY N RDNG THS SNTNC.”
Words can be redundant: “the” is almost always a grammatical formality, and it can usually be erased with little cost to our understanding. Poe’s cryptographic pirate would have been wise to slash the redundancy of his message by cutting every instance of “the,” or “;48”—it was the very opening that Mr. Legrand exploited to such effect. Entire messages can be redundant: in all of those weighted-coin cases in which our answers are all but known in advance, we can speak and speak and say nothing new. On Shannon’s understanding of information, the redundant symbols are all of the ones we can do without—every letter, word, or line that we can strike with no damage to the information.
As his approximations of text grew more and more like English, then, they also grew more and more redundant. And if this redundancy grows out of the rules that check our freedom, it is also dictated by the practicalities of communicating with one another. Every human language is highly redundant. From the dispassionate perspective of the information theorist, the majority of what we say—whether out of convention, or grammar, or habit—could just as well go unsaid. In his theory of communication, Shannon guessed that the world’s wealth of English text could be cut in half with no loss of information: “When we write English, half of what we write is determined by the structure of the language and half is chosen freely.” Later on, his estimate of redundancy rose as high as 80 percent: only one in five characters actually bear information.
As it is, Shannon suggested, we’re lucky that our redundancy isn’t any higher. If it were, there wouldn’t be any crossword puzzles. At zero redundancy, in a world in which RXKHRJFFJUJ is a word, “any sequence of letters is a reasonable text in the language and any two dimensional array of letters forms a crossword puzzle.” At higher redundancies, fewer sequences are possible, and the number of potential intersections shrinks: if English were much more redundant, it would be nearly impossible to make puzzles. On the other hand, if English were a bit less redundant, Shannon speculated, we’d be filling in crossword puzzles in three dimensions.
Shannon’s estimates of our language’s redundancy grew, he wrote cryptically, out of “certain known results in cryptography.” The hint he dropped there is a reminder that his great work on code writing, “Communication Theory of Secrecy Systems,” was still classified in 1948. Other sources, though, Shannon could discuss more openly. One was Raymond Chandler.
One evening, Shannon picked up Chandler’s pulpy book of detective stories, Pickup on Noon Street, and flipped, as he often did in those days, to a random passage. His job was to spell the text out letter by letter; the job of his assistant was to guess the next letter until she got it right. By the time they arrived at “A S-M-A-L-L O-B-L-O-N-G R-E-A-D-I-N-G L-A-M-P O-N T-H-E D” she could guess the next three letters with perfect accuracy. E-S-K.
The point was not the assistant’s powers of prediction—it was that any English reader would be just as clairvoyant in the same position, reading the same sentence governed by the same silent rules. By the time the reader has reached D, she has already gotten the point. E-S-K is a formality; and if the rules of our language left us free to shut up once the point has been gotten, D would be enough. The redundancy went even further. A phrase beginning “a small oblong reading lamp on the” is almost certainly followed by one of two letters: D, or the first guess, T. In a zero-redundancy language, the assistant would have had just a 1-in-26 chance of guessing what came next, and so the next letter would have been as informative as possible. In our language, though, her odds were much closer to 1-in-2, and the letter bore far less information. And even further: the Oxford English Dictionary lists 228,132 words. Out of that twenty-volume trove of lexicography, two words were hugely probable after the short phrase that Shannon spelled out: “desk”; “table.” Once Raymond Chandler got to “the,” he had written himself into a corner. Not that he bore any fault for it: we all write and talk and sing ourselves into corners as a condition of writing and talking and singing.
Understanding redundancy, we can manipulate it deliberately, just as an earlier era’s engineers learned to play tricks with steam and heat.
Of course, humans had been experimenting with redundancy in their trial-and-error way for centuries. We cut redundancy when we write shorthand, when we assign nicknames, when we invent jargon to compress a mass of meaning (“the left-hand side of the boat when you’re facing the front”) into a single point (“port”). We add redundancy when we say “V as in Victor” to make ourselves more clearly heard, when we circumlocute around the obvious, even when we repeat ourselves. But it was Shannon who showed the conceptual unity behind all of these actions and more.
At the foundation of our Information Age—once wires and microchips have been stripped away, once the stream of 0’s and 1’s has been parted—we find Shannon’s two fundamental theorems of communication. Together they speak to the two ways in which we can manipulate redundancy: subtracting it, and adding it.
To begin with, how fast can we send a message? It depends, Shannon showed, on how much redundancy we can wring out of it. The most efficient message would actually resemble a string of random text: each new symbol would be as informative as possible, and thus as surprising as possible. Not a single symbol would be wasted. Of course, the messages that we want to send one another—whether telegraphs or TV broadcasts—do “waste” symbols all the time. So the speed with which we can communicate over a given channel depends on how we encode our messages: how we package them, as compactly as possible, for shipment. Shannon’s first theorem proves that there is a point of maximum compactness for every message source. We have reached the limits of communication when every symbol tells us something new. And because we now have an exact measure of information, the bit, we also know how much a message can be compressed before it reaches that point of perfect singularity. It was one of the beauties of a physical idea of information, a bit to stand among meters and grams: proof that the efficiency of our communication depends not just on the qualities of our media of talking, on the thickness of a wire or the frequency range of a radio signal, but on something measurable, pin-downable, in the message itself.
What remained, then, was the work of source coding: building reliable systems to wring the excess from our all-too-humanly redundant messages at the source, and to reconstitute them at the destination. Shannon, along with MIT engineer Robert Fano, made an important start in this direction, and in an encyclopedia article he wrote some time after his famous paper, Shannon explained how a simple redundancy-eliminating code would work. It all depends, he said, on the statistical nature of messages: on the probability with which a white pixel happens next to a white pixel in an image, or on the frequencies of letters and digrams and trigrams that made those randomly generated fragments look more and more like English. Imagine that our language has only four letters: A, B, C, and D. Imagine that this language, like every other, lazes itself into patterns over time. Over time, half of the letters turn out to be A, a quarter turn out to be B, and C and D each make up an eighth. If we wanted to send a message in this language over the airwaves in 0’s and 1’s, what is the best code we could use?
Perhaps we opt for the obvious solution: each letter gets the same number of bits. For a four-letter language, we’d need two bits for each letter:
A = 00
B = 01
C = 10
D = 11
But we can do better. In fact, when transmission speed is such a valuable commodity (consider everything you can’t do with a dial-up modem), we have to do better. And if we bear in mind the statistics of this particular language, we can. It’s just a matter of using the fewest bits on the most common letters, and using the most cumbersome strings on the rarest ones. In other words, the least “surprising” letter is encoded with the smallest number of bits. Imagine, Shannon suggested, that we tried this code instead:
A = 0
B = 10
C = 110
D = 111III
To prove that this code is more efficient, we can multiply the number of bits for each letter by the chance that each letter will occur, giving us an average of bits per letter:
(1/2)•1 + (1/4)•2 + (1/8)•3 + (1/8)•3 = 1.75.
The message sent with this second code is less redundant: rather than using 2 bits per letter, we can express an identical idea with a leaner 1.75. It turns out that 1.75 is a special number in this four-letter language—it’s also the amount of information, in bits, of any letter. Here, then, we’ve reached the limit. For this language, it’s impossible to write a more efficient code. It’s as information-dense as possible: not a digit is wasted. Shannon’s first theorem shows that more complex sources—audio, video, TV, Web pages—can all be efficiently compressed in similar, if far more complex, ways.
Codes of this kind—pioneered by Shannon and Fano, and then improved by Fano’s student David Huffman and scores of researchers since then—are so crucial because they enormously expand the range of messages worth sending. If we could not compress our messages, a single audio file would take hours to download, streaming Web video would be impossibly slow, and hours of television would demand a bookshelf of tapes, not a small box of discs. Because we can compress our messages, video files can be compacted to just a twentieth of their size. All of this communication—faster, cheaper, more voluminous—rests on Shannon’s realization of our predictability. All of that predictability is fat to be cut; since Shannon, our signals have traveled light.
Yet they also travel under threat. Every signal is subject to noise. Every message is liable to corruption, distortion, scrambling, and the most ambitious messages, the most complex pulses sent over the greatest distances, are the most easily distorted. Sometime soon—not in 1948, but within the lifetimes of Shannon and his Bell Labs colleagues—human communication was going to reach the limits of its ambition, unless noise could be solved.
That was the burden of Shannon’s second fundamental theorem. Unlike his first, which temporarily excised noise from the equation, the second presumed a realistically noisy world and showed us, within that world, the bounds of our accuracy and speed. Understanding those bounds demanded an investigation not simply of what we want to say, but of our means of saying it: the qualities of the channel over which our message is sent, whether that channel is a telegraph line or a fiber-optic cable.
Shannon’s paper was the first to define the idea of channel capacity, the number of bits per second that a channel can accurately handle. He proved a precise relationship between a channel’s capacity and two of its other qualities: bandwidth (or the range of frequencies it could accommodate) and its ratio of signal to noise. Nyquist and Hartley had both explored the trade-offs among capacity, complexity, and speed; but it was Shannon who expressed those trade-offs in their most precise, controllable form. The groundbreaking fact about channel capacity, though, was not simply that it could be traded for or traded away. It was that there is a hard cap—a “speed limit” in bits per second—on accurate communication in any medium. Past this point, which was soon enough named the Shannon limit, our accuracy breaks down. Shannon gave every subsequent generation of engineers a mark to aim for, as well as a way of knowing when they were wasting their time in pursuit of the hopeless. In a way, he also gave them what they had been after since the days of Thomson and the transatlantic cable: an equation that brought message and medium under the same laws.
This would have been enough. But it was the next step that seemed, depending on one’s perspective, miraculous or inconceivable. Below the channel’s speed limit, we can make our messages as accurate as we desire—for all intents, we can make them perfectly accurate, perfectly free from noise. This was Shannon’s furthest-reaching find: the one Fano called “unknown, unthinkable,” until Shannon thought it.
Until Shannon, it was simply conventional wisdom that noise had to be endured. The means of mitigating noise had hardly changed, in principle, since Wildman Whitehouse fried the great undersea cable. Transmitting information, common sense said, was like transmitting power. Expensively and precariously adding more power remained the best answer—shouting through the static, as it were, brute-forcing the signal-to-noise ratio by pumping out a louder signal.
Shannon’s promise of perfect accuracy was something radically new.IV For engineering professor James Massey, it was this promise above all that made Shannon’s theory “Copernican”: Copernican in the sense that it productively stood the obvious on its head and revolutionized our understanding of the world. Just as the sun “obviously” orbited the earth, the best answer to noise “obviously” had to do with physical channels of communication, with their power and signal strength. Shannon proposed an unsettling inversion. Ignore the physical channel and accept its limits: we can overcome noise by manipulating our messages. The answer to noise is not in how loudly we speak, but in how we say what we say.
How did the faltering transatlantic telegraph operators attempt to deal with the corruption of their signal? They simply repeated themselves: “Repeat, please.” “Send slower.” “Right. Right.” In fact, Shannon showed that the beleaguered key-tappers in Ireland and Newfoundland had essentially gotten it right, had already solved the problem without knowing it. They might have said, if only they could have read Shannon’s paper, “Please add redundancy.”
In a way, that was already evident enough: saying the same thing twice in a noisy room is a way of adding redundancy, on the unstated assumption that the same error is unlikely to attach itself to the same place two times in a row. For Shannon, though, there was much more. Our linguistic predictability, our congenital failure to maximize information, is actually our best protection from error. A few pages ago, recall, you read that the structure of our language denies us total freedom to choose “the next letter and the next pineapple.” As soon as you reached “pineapple”—really, as soon as you got to “p”—you knew that something was wrong. You had detected (and probably corrected) an error. You did it because, even without running the numbers, you have an innate grasp of the statistical structure of English. And that intuition told you that the odds of “pineapple” making sense in that sentence and paragraph were lottery-winning low. The redundancy of our language corrected the error for you. On the other hand, imagine how much harder it would be to find an error in the “XFOML” language, a language in which each letter is equally likely.V
For Shannon, then, the key was once again in the code. We must be able to write codes, he showed, in which redundancy acts as a shield: codes in which no one bit is indispensable, and thus codes in which any bit can absorb the damage of noise. Once more, we want to send a message made up of the letters A through D, but this time we are less concerned with compressing the message than with passing it safely through a noisy channel. Again, we might start by trying the laziest code:
A = 00
B = 01
C = 10
D = 11
One of the worst things that noise can do—in a burst of static, interference from the atmosphere, or physical damage to the channel—is falsify bits. Where the sender says “1,” the receiver hears “0,” or vice versa. So if we used this code, an error to a single bit could be fatal. If just one of the bits representing C flipped, C would vanish in the channel: it would emerge as B or D, with the receiver none the wiser. It would take just two such flips to turn “DAD” to “CAB.”
But we can solve the problem—just as human languages have intuitively, automatically solved the same problem—by adding bits. We could use a code like this:
A = 00000
B = 00111
C = 11100
D = 11011
Now any letter could sustain damage to any one bit and still resemble itself more than any other letter. With two errors, things get fuzzier: 00011 could be either B with one flipped bit or A with two. But it takes fully three errors to turn one letter into another. Our new code resists noise in a way our first one did not, and does it more efficiently than simple repetition. We were not forced to change a single thing about our medium of communication: no yelling across a crowded room, no hooking up spark coils to the telegraph, no beaming twice the television signal into the sky. We only had to signal smarter.
As long as we respect the speed limit of the channel, there is no limit to our accuracy, no limit to the amount of noise through which we can make ourselves heard. Yes, overcoming more errors, or representing more characters, would demand more complex codes. So would combining the advantages of codes that compress and codes that guard against error: that is, reducing a message to bits as efficiently as possible, and then adding the redundancy that protects its accuracy. Coding and decoding would still exact their cost in effort and time. But Shannon’s proof stood: there is always an answer. The answer is digital. Here Shannon completed the reimagining that began with his thesis and his switches eleven years earlier. 1’s and 0’s could enact the entirety of logic. 1’s and 0’s stood for the fundamental nature of information, an equal choice from a set of two. And now it was evident that any message could be sent flawlessly—we could communicate anything of any complexity to anyone at any distance—provided it was translated into 1’s and 0’s. Logic is digital. Information is digital.
So each message is kin to all messages. “Up until that time, everyone thought that communication was involved in trying to find ways of communicating written language, spoken language, pictures, video, and all of these different things—that all of these would require different ways of communicating,” said Shannon’s colleague Robert Gallager. “Claude said no, you can turn all of them into binary digits. And then you can find ways of communicating the binary digits.” You can code any message as a stream of bits, without having to know where it will go; you can transmit any stream of bits, efficiently and reliably, without having to know where it came from. As information theorist Dave Forney put it, “bits are the universal interface.”
In time, the thoughts developed in these seventy-seven pages in the Bell System Technical Journal would give rise to a digital world: satellites speaking to earth in binary code, discs that could play music through smudges and scratches (because storage is just another channel, and a scratch is just another noise), the world’s information distilled into a black rectangle two inches across.
In time: because while Shannon had proven that the codes must be there, neither he nor anyone else had shown what they must be. Once the audacity of his work had worn off—he had, after all, founded a new field and solved most of its problems at one stroke—one consequential shortfall would dominate the conversation on Claude Shannon and Claude Shannon’s theory. How long would it take to find the codes? Once found, would they even make everyday practical sense, or would it simply be cheaper to continue muddling through? Could this strange work, full of imaginary languages, messages without meaning, random text, and a philosophy that claimed to encompass and explain every signal that could possibly be sent, ever be more than an elegant piece of theorizing? In words with which any engineer could have sympathized: would it work?
Yet, from the other direction and in a far different spirit, there came another set of questions. They’re best overheard in a conversation between Shannon and Von Neumann at Princeton, said to have taken place in 1940, when Shannon was first piecing his theory together in the midst of his failing marriage. Shannon approached the great man with his idea of information-as-resolved-uncertainty—which would come to stand at the heart of his work—and with an unassuming question. What should he call this thing? Von Neumann answered at once: say that information reduces “entropy.” For one, it was a good, solid physics word. “And more importantly,” he went on, “no one knows what entropy really is, so in a debate you will always have the advantage.”
Almost certainly, this conversation never happened. But great science tends to generate its own lore, and the story is almost coeval with Shannon’s paper. It was retold in seminars and lectures and books, and Shannon himself had to brush it away at conferences and in interviews with his usual evasive laugh. The story was retold for so long—as we are retelling it here—just because the link between information and entropy was so suggestive.VI From one direction came the demand that Shannon’s paper work; from the other, the suspicion that it hinted at truths more profound than the author himself was willing to admit.
No one knows what entropy really is. It was an overstatement; but entropy has, at least, been a multitude of things in its conceptual life—nearly as many things as information itself—some scientifically sound, and some otherwise. It has been the inability of a steam engine to do work; it has been the dissipation of heat and energy, the unalterable tendency of every part of a closed system to lapse toward lukewarm muck; it has been, more roughly but also more resonantly, the trend toward disorder, chaos. It is the always incipient mess against which we are pitted as a condition of living. James Gleick put this succintly: “Organisms organize.” He went on:
We sort the mail, build sand castles, solve jigsaw puzzles, separate wheat from chaff, rearrange chess pieces, collect stamps, alphabetize books, create symmetry, compose sonnets and sonatas, and put our rooms in order. . . . We propagate structure (not just we humans but we who are alive). We disturb the tendency toward equilibrium. It would be absurd to attempt a thermodynamic accounting for such processes, but it is not absurd to say that we are reducing entropy, piece by piece. Bit by bit.
In pursuing all of this order, we render our world less informative, because we reduce the amount of uncertainty available to be resolved. The predictability of our communication is, in this light, the image of a greater predictability. We are, all of us, predictability machines. We think of ourselves as incessant makers and consumers of information. But in the sense of Shannon’s entropy, the opposite is true: we are sucking information out of the world.
Yet we are failing at it. Heat dissipates; disorder, in the very long run, increases; entropy, the physicists tell us, runs on an eternally upward slope. In the state of maximal entropy, all pockets of predictability would have long since failed: each particle a surprise. And the whole would read, were there then eyes to read it, as the most informative of messages.
The unsettled question: whether information-as-entropy was a misplaced and fruitless analogy, or whether it was a more or less resonant language in which to talk about the world—or whether, in fact, information itself was fundamental in a way that even a physicist could appreciate. When particles jump from state to state, is their resemblance to switches, to logic circuits, to 0’s and 1’s, something more than a trick of our eyes? Or put it this way: Was the quality of information something we imposed on the world, just a by-product of our messages and machines—or was it something we found out about the world, something that had been there all along?
These were only some of the insistent questions that trailed after Shannon’s theory. Shannon himself—even while courting them with the use of such a tantalizing term, or metaphor, as “entropy”—almost always dismissed these puzzles. His was a theory of messages and transmission and communication and codes. It was enough. “You know where my interests are.”
But in his insistence on this point, he ran up against a human habit much older than him: our tendency to reimagine the universe in the image of our tools. We made clocks, and found the world to be clockwork; steam engines, and found the world to be a machine processing heat; information networks—switching circuits and data transmission and half a million miles of submarine cable connecting the continents—and found the world in their image, too.
I. Because you’re unconsciously aware of those rules, you’ve already recognized “pineapple” as a transmission error. Given the way the paragraph and the sentence were developing, practically the only word possible in that location was “word.”
II. In an unpublished spoof written a year later, Shannon imagined the damage his methods would do if they fell into the wrong hands. It seems that an evil Nazi scientist, Dr. Hagen Krankheit, had escaped Germany with a prototype of his Müllabfuhrwortmaschine, a fearsome weapon of war “anticipated in the work . . . of Dr. Claude Shannon.” Krankheit’s machine used the principles of randomized text to totally automate the propaganda industry. By randomly stitching together agitprop phrases in a way that approximated human language, the Müllabfuhrwortmaschine could produce an endless flood of demoralizing statements. On one trial run, it spat out “Subversive elements were revealed to be related by marriage to a well-known columnist,”“Capitalist warmonger is a weak link in atomic security,” and “Atomic scientist is said to be associated with certain religious and racial groups.” Remarkably, these machine-generated phrases were indistinguishable from human propaganda—and now it was feared that the machine had fallen into the hands of the communists.
III. Why not use 11 for C? In that case, it would be impossible to unambiguously decode a multi-symbol message. 1110, for instance, could mean either “CB” or “DA.”
IV. Or more accurately, of an “arbitrarily small” rate of error: an error rate as low as we want, and want to pay for.
V. Kahn illustrates this point with a useful thought experiment. Think of a language in which any four-letter combination, from “aaaa” to “zzzz,” was fair game. There would be 456,976 such combinations, more than enough to account for every word in an English dictionary. But when any letter combination is valid, recognizing errors becomes far more difficult. “ ‘Xfim,’ meaning perhaps ‘come,’ would be changed to ‘xfem,’ maybe meaning ‘go’ and, without redundancy, no alarm bells would ring.” By contrast, ordinary languages benefit not just from the redundancy of context (which made “pineapple” impossible above), but from the redundancy of letters that bear no information. The loss of one dot in Morse code turns “individual” into “endividual”—but the error is easy to detect. Most English words can suffer similar errors to several letters before the sender’s intention is lost.
VI. The link between information and entropy was made explicit in Shannon’s paper. But a connection between information and physics was first suggested, as early as 1929, by the Hungarian physicist Leo Szilard. Briefly, Szilard resolved an old puzzle in the physics of heat: the Second Law of Thermodynamics says that entropy is constantly increasing, but what if we imagined a microscopic and intelligent being, which James Clerk Maxwell had dubbed a “demon,”that tried to decrease entropy by sorting hot molecules from cold? Would that contradict the Second Law? Szilard showed that it would not: the very act of determining which molecules were which would cost enough energy to offset any savings that Maxwell’s Demon proposed to achieve. In other words—learning information about particles costs energy. Shannon, however, had not read Szilard’s work when he wrote his 1948 paper.