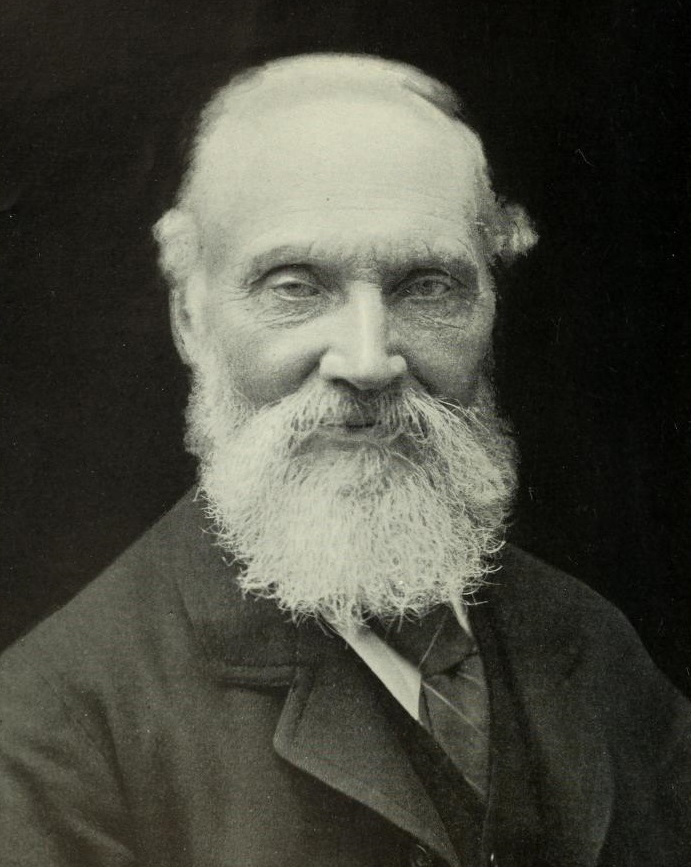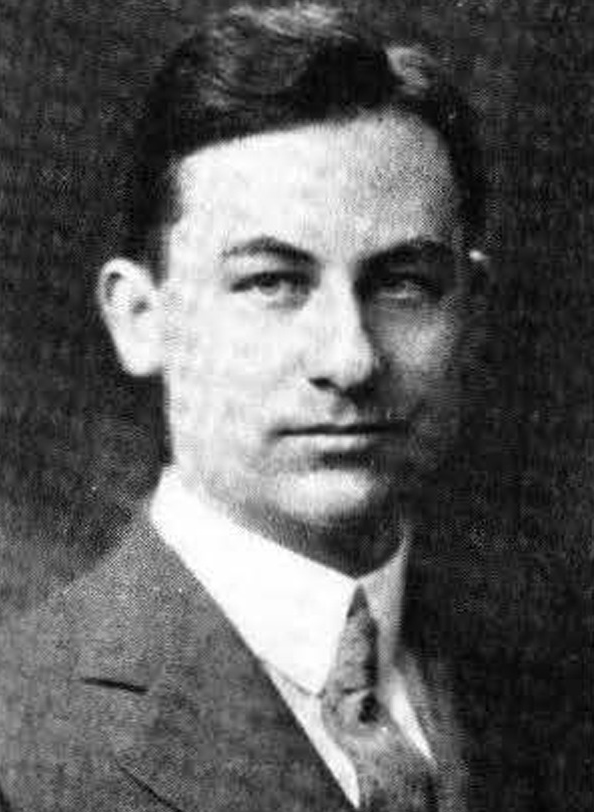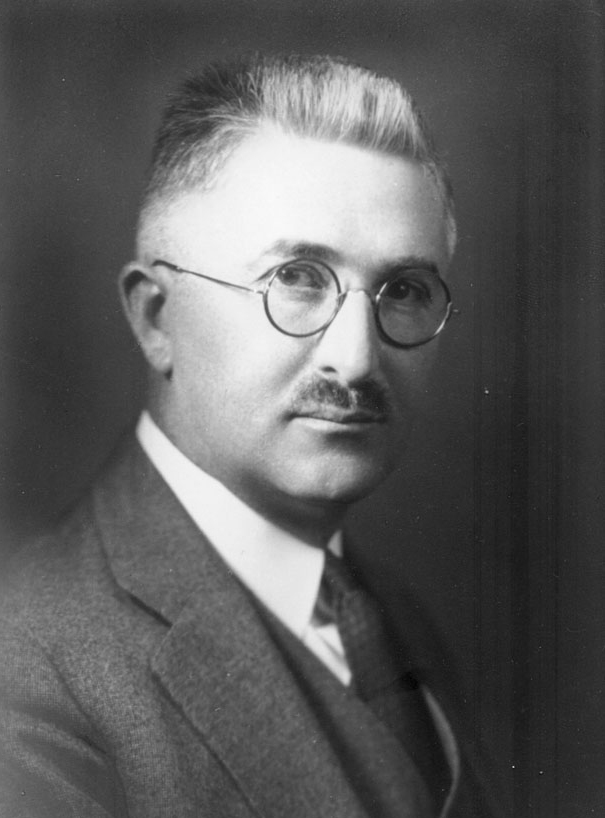Photographs
1
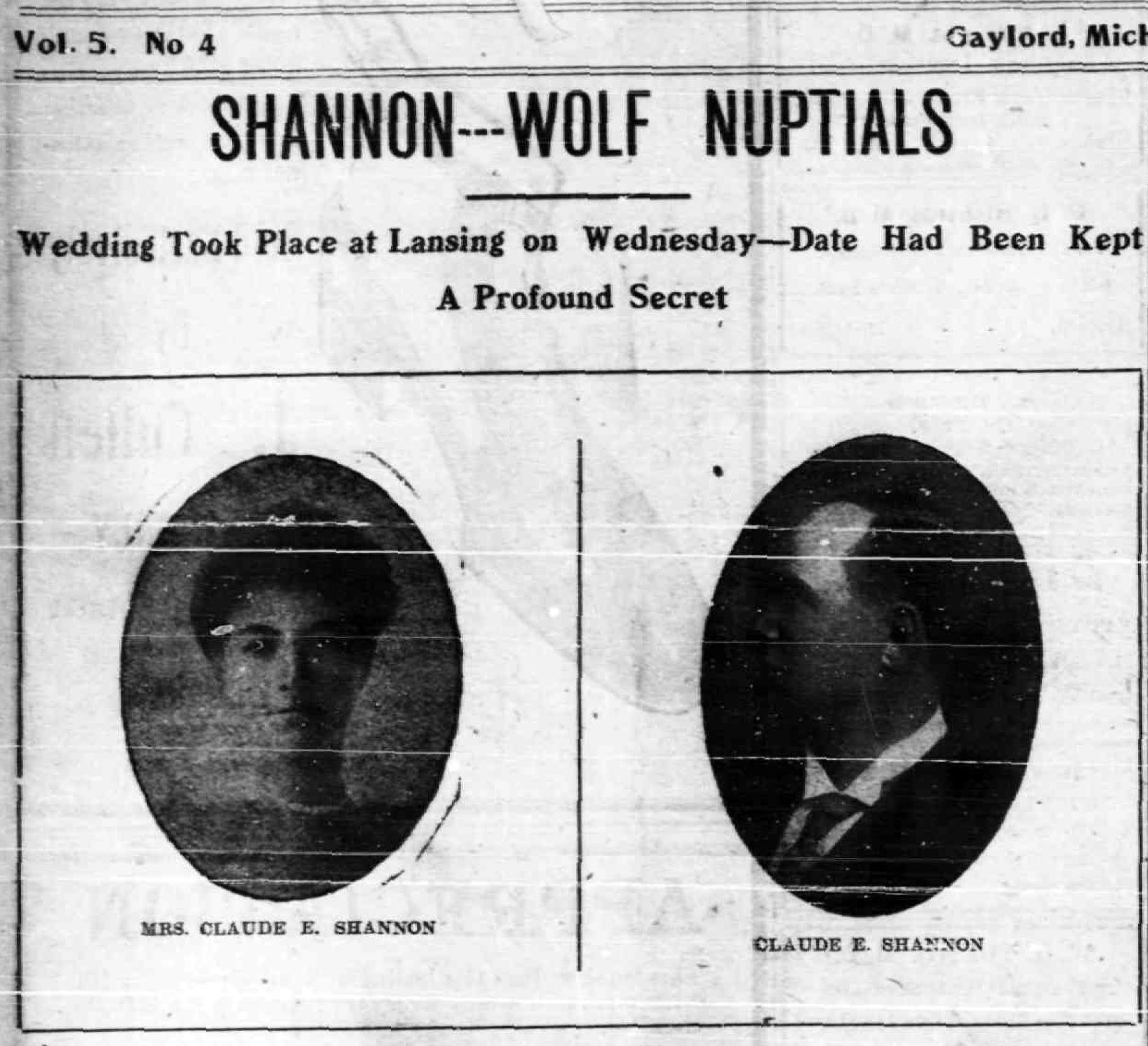
Born in 1862 in New Jersey, Claude Shannon’s father, Claude Elwood Shannon Sr., worked as a furniture salesman, funeral director, and probate judge. Claude’s mother, born Mabel Wolf, was the daughter of a German immigrant; she was a teacher and school principal. Their 1909 wedding announcement was front-page news in Gaylord, testament both to the town’s smallness and the Shannons’ active roles in the community.

2
By the time Claude Shannon took this registration photo for the University of Michigan, he was already an accomplished tinkerer. His creations included a makeshift elevator, a backyard trolley, and a telegraph system that sent coded messages along a barbed-wire fence.
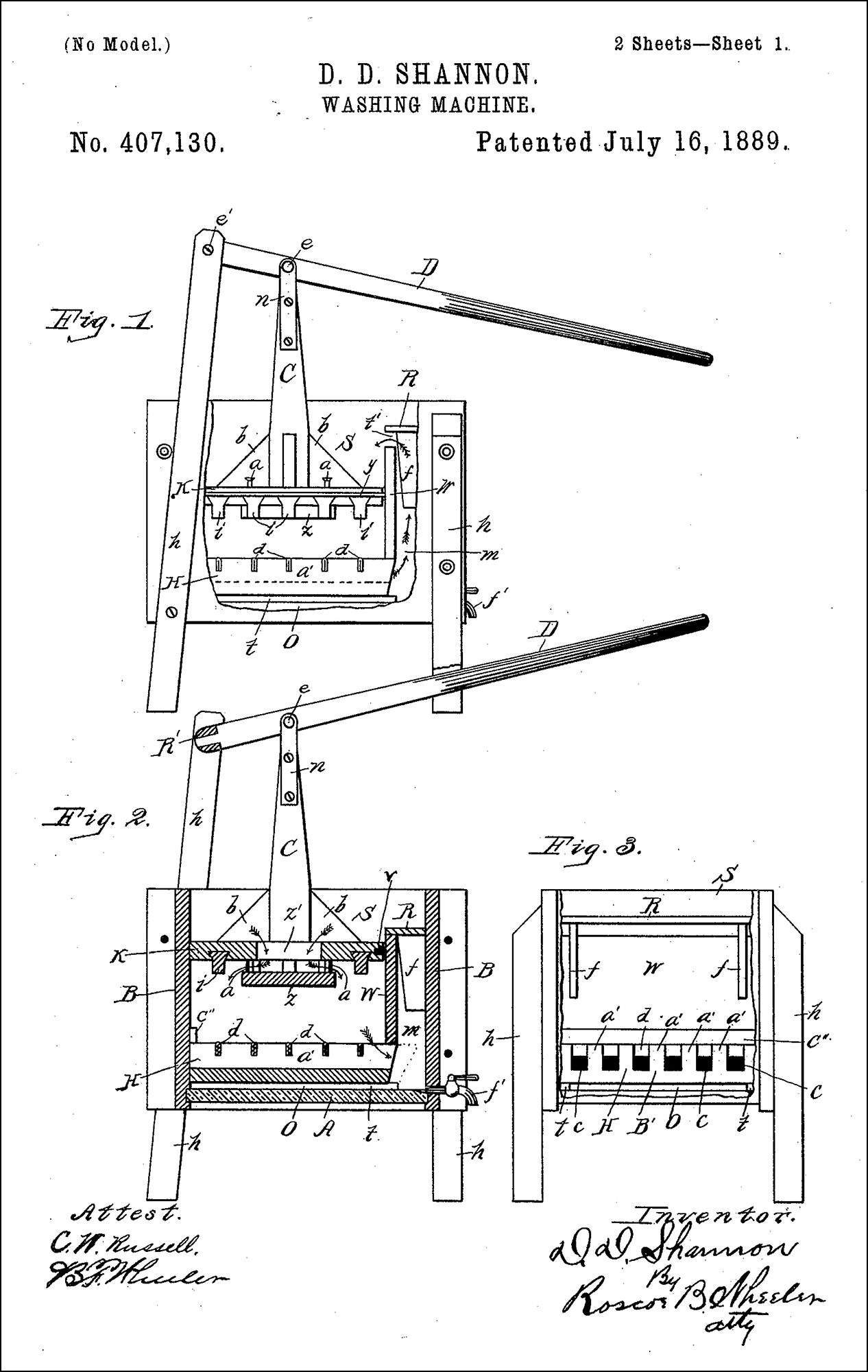
3
Shannon appears to have taken after his grandfather David Shannon Jr., the proud owner of U.S. Patent No. 407,130, a series of improvements on the washing machine. For a boy of Claude Jr.’s mechanical bent, a certified inventor in the family tree was something to brag about.
4
The University of Michigan’s College of Engineering had grown dramatically in the years before Shannon’s arrival. At one of its public exhibitions, students “surprised their visitors by sawing wood with a piece of paper running at 20,000 revolutions per minute, freezing flowers in liquid air, and showing a bottle supported only by two narrow wires from which a full stream of water flowed—a mystery solved by few.” Michigan’s engineering buildings were fitted out for heavy industry. They included this foundry . . .
5
. . . and this naval tank, where students tested the hydrodynamics of model ships.
6
In the spring of 1934, at the age of seventeen, Claude Shannon claimed his first publication credit, on page 191 of the American Mathematical Monthly. Shannon’s contribution was the solution to a math puzzle. That he was reading such a journal at all hints at more than the usual attention paid to academic matters; that his solution was chosen points to more than the usual talent.
7
The campus of MIT, where Shannon first made his name as an engineer, was a compromise between architects: a classical dome sitting atop tunnels built for “efficiency and avoidance of lost motion by student and teacher, equal to that which obtains in our best industrial works.” It was part temple and part factory.
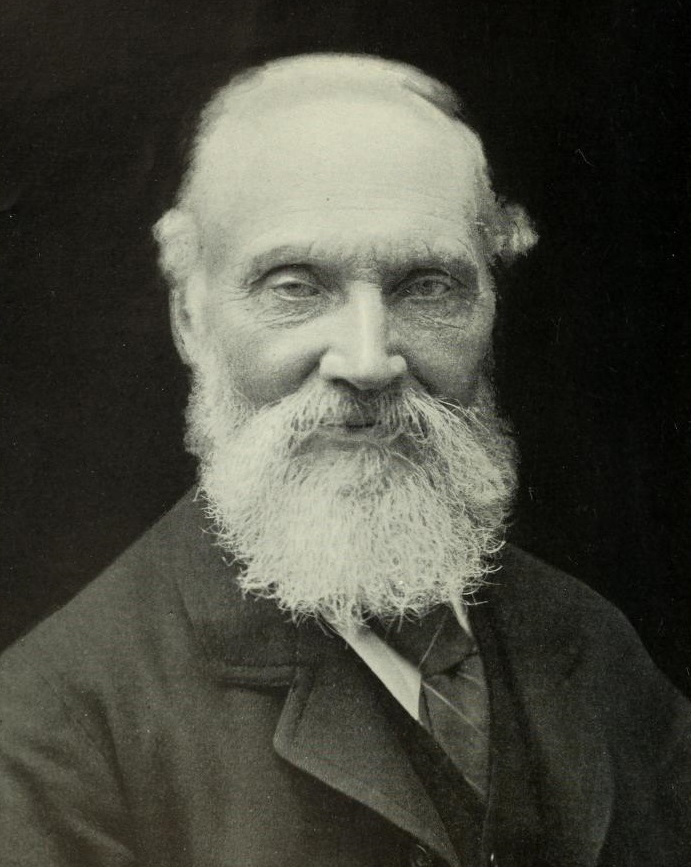
8
At MIT, Shannon joined a team dedicated to managing the differential analyzer: an all-purpose mechanical computer capable of bringing the force of calculus to bear on the industrial problems of power transmission or telephone networks, or on the advanced physics problems of cosmic rays and subatomic particles. The project followed in the footsteps of the wizard-bearded physicist William Thomson, Lord Kelvin, who built an early mechanical computer in 1876.
9
At MIT, Shannon trained as a pilot in his spare time. The professor who taught the flying class urged MIT’s president to ban him from taking further lessons: such a brain was too valuable to risk in a crash. The president refused: “Somehow I doubt the advisability of urging a young man to refrain from flying or arbitrarily to take the opportunity away from him, on the ground of his being intellectually superior.”
10
The differential analyzer: a brain the size of a room that could whir away at a problem for days and nights on end. “It was a fearsome thing of shafts, gears, strings, and wheels rolling on disks—but it worked.”

11
Vannevar Bush was, by most accounts, the most powerful scientist in mid-twentieth-century America. He presided over the differential analyzer at MIT, advised presidents, and led America’s scientists through World War II. Collier’s magazine called him “the man who may win or lose the war”; Time, “the general of physics.” And not least among these accomplishments was this: he became Claude Shannon’s first and most influential mentor.

12
Traveling to Cold Spring Harbor in the summer of 1939, Shannon arrived at one of the greatest genetics laboratories in America, and one of the greatest scientific embarrassments: the Eugenics Record Office. It housed a treasury of genetic data, which Shannon drew on for his dissertation on theoretical genetics.
13
Shannon’s fellowship at the Institute for Advanced Study in Princeton was prestigious, but less than gratifying: it saw the breakdown of his first marriage and his growing fears about the WWII draft, though it also included a number of run-ins with Albert Einstein.

14
This was the Bell Labs complex as seen from Washington Street in Manhattan’s West Village in 1936. “People did very well at Bell Labs,” recalled one of Shannon’s colleagues, “when they did what others thought was impossible.” Shannon signed up for a full-time job when its offices were still in lower Manhattan, near the site of the present-day High Line.
15
Claude Shannon and his colleague Dave Hagelbarger at work at Bell Labs. As another colleague would remark about that time at Bell: “Here I am, I’ve got the world’s knowledge in electrical engineering at my beck and call. All I’ve got to do is pick up the phone or go see somebody and I can get the answer.”
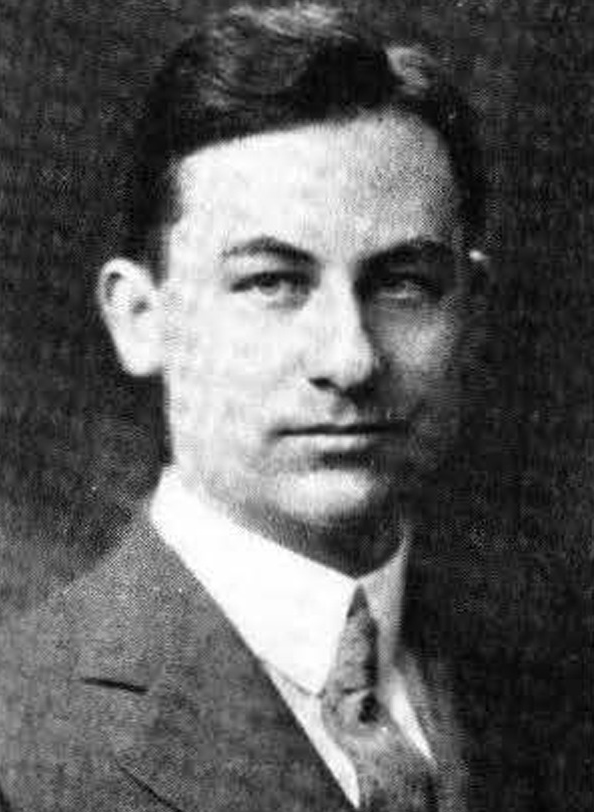
16
Thornton Fry founded the Labs’ math group and assigned Shannon to it. “Mathematicians are queer people,” he once said. “That’s a fact. So that anybody who was queer enough that you didn’t know what to do with him, you said, ‘This fellow is a mathematician. Let’s have him transferred over to Fry.’ ”
17
Along with Barney Oliver, Shannon and John Pierce (pictured here) formed a genius clique of three at the Labs. As a contemporary joked, “the three of those people were intellectually insufferable.”
18
In Manhattan, Shannon was a bachelor—after the end of his brief first marriage—with a small Greenwich Village apartment and a demanding job. He kept odd hours, played music too loud, and relished the New York jazz scene.

19
As part of the “scientists’ war” against Nazi Germany, Shannon contributed to research on cryptography, antiaircraft fire control, and SIGSALY (pictured here), the most ambitious speech-scrambling system of its day.
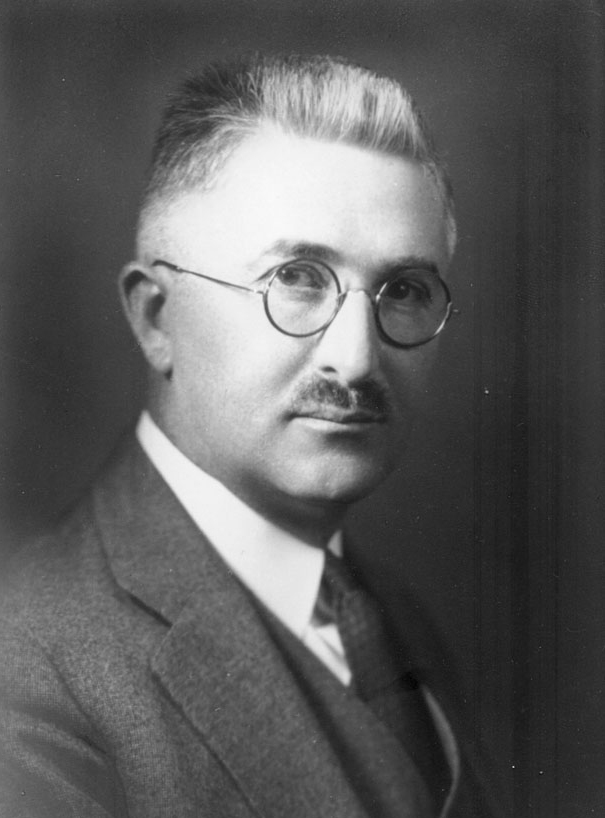
20
No one was more influential to Shannon’s work on information theory than Ralph Hartley. His 1927 paper on the “Transmission of Information” was the closest approach to date to capturing the essence of information, explaining how scientists might begin to think of it physically rather than psychologically.

21
Before Shannon’s 1948 “A Mathematical Theory of Communication,” a century of common sense and engineering trial and error said that noise—the physical world’s tax on our messages—had to be lived with. Shannon proved that noise could be defeated, that information sent from Point A could be received with perfection at Point B, not just often, but essentially always. He gave engineers the conceptual tools to digitize information and send it flawlessly, a result considered hopelessly utopian up until the moment Shannon proved it was not.

22
After 1948, Shannon was heralded by the media as a noteworthy figure in the world of science. He gave television interviews, was written up in national publications, and received honorary degrees.

23
In 1948, Claude Shannon struck up a conversation with Betty Moore, a fellow Bell Labs employee, and summoned the courage to ask her out to dinner. That dinner led to a second, the second to a third, until they were dining together every night.

24
Claude and Betty Shannon’s courtship was efficient: they met in the fall of 1948, and by early 1949, Claude had proposed—in his “not very formal” way, as Betty recalled. She shared not only his sense of humor but his love of math—the foundation of a partnership that would last the rest of Claude’s life.

25
Betty purchased Claude’s first unicycle, sparking his lifelong fascination with the machines. He would build and customize unicycles of his own, ride them through the narrow Bell Labs hallways, and impress visitors with his agility.

26
Even at the height of his scientific celebrity, Shannon remained a tinkerer. His most famous creation, Theseus, was an artificial, maze-solving mouse that could “learn” the location of a metallic piece of cheese. (When the cheese was removed, Theseus could only wander the maze aimlessly. As another scientist observed, “It is all too human.”)
28
Bell Labs’ Murray Hill campus, “where the future, which is what we now happen to call the present, was conceived and designed.”
29
Shannon built one of the world’s earliest chess-playing machines. Completed in 1949, Shannon’s machine handled six pieces and focused on the game’s final moves. More than 150 relay switches were used to calculate a move, processing power that allowed the machine to decide within a respectable ten to fifteen seconds.

30
“I’m a machine and you’re a machine, and we both think, don’t we?”
31
Shannon set four goals for artificial intelligence to achieve by 2001: a chess-playing program that was crowned world champion, a poetry program that had a piece accepted by the New Yorker, a mathematical program that proved the elusive Riemann hypothesis, and, “most important,” a stock-picking program that outperformed the prime rate by 50 percent. “These goals,” he said only half-jokingly, “could mark the beginning of a phase-out of the stupid, entropy-increasing, and militant human race in favor of a more logical, energy conserving, and friendly species—the computer.”
32
Norbert Wiener (pictured in the center with Shannon and MIT president Julius Stratton on the left) was a former child prodigy, the inventor of “cybernetics,” and the only scientist who could plausibly challenge Shannon’s claim to have founded information theory.
33
Claude and Betty purchased a house in Winchester, Massachusetts, a bedroom community eight miles north of MIT. Built in 1858, the house was constructed for Ellen Dwight, a great-granddaughter of Thomas Jefferson. Originally seated on twelve acres, its design was inspired by Monticello.
34
On a trip to Russia, Shannon offered a friendly chess game to a Soviet champion, Mikhail Botvinnik. Botvinnik only took a serious interest in the game when Shannon managed to win the favorable exchange of his knight and a pawn for Botvinnik’s rook. After forty-two moves, Shannon tipped his king over, conceding the match. But lasting dozens of moves against Botvinnik, considered among the most gifted chess players of all time, earned Shannon lifelong bragging rights.
35
In 1957, Shannon returned to MIT as a professor. He attracted somewhat less than his share of graduate students: as one observed, “You had to have a pretty big ego to ask someone like Shannon to supervise you!”
36
On February 6, 1967, President Lyndon B. Johnson presented Claude Shannon with the National Medal of Science in honor of his “brilliant contributions to the mathematical theories of communications and information processing.”

37
Shannon’s early MIT lectures on information theory attracted packed houses, but none drew a bigger crowd than his talk on the stock market, which he delivered to an overflowing crowd in the university’s largest lecture hall.

38
In Massachusetts, Professor Shannon grew a beard and took up jogging. He also fully indulged his tinkering habit: many of his best-known creations were devised in an extensive home workshop.

39
What was arguably world’s first wearable computer was developed by Shannon and Edward Thorp to calculate roulette odds. After several successful test runs at Las Vegas casinos, they abandoned the project out of fear of provoking a run-in with the Mafia.

40
Assembled from Shannon’s erector set and modeled on W. C. Fields, this robot could bounce-juggle three balls. The balls rebounded off a tom-tom drum, and the robot moved its paddle arms in a rocking motion, “each side making a catch when it rocks down and a toss when it rocks up.”

41
Shannon was both a skilled juggler himself and the author of the first serious paper on the mathematics of juggling. He wrote that his readers should “try not to forget the poetry, the comedy and the music of juggling. . . . Does this sound pretentious?”

42
Shannon kept up his unicycling hobby well into his later years.

43
Shannon’s was a life spent in pursuit of curious, serious play; he was that rare scientific genius who was just as content rigging up a juggling robot or a flamethrowing trumpet as he was pioneering digital circuits.

44

45
Shannon delighted in the curiosities that grabbed his attention. He could find himself lost in the intricacies of an engineering problem, and then, just as suddenly, become captivated by a chess position. He turned arid and technical sciences into vast and captivating puzzles, the solving of which was play of the adult kind.