CS 257 (Fall 2000) Project 1: E. coli we hardly knew ye. *

Problem 1 (Bacterial Chemotaxis)
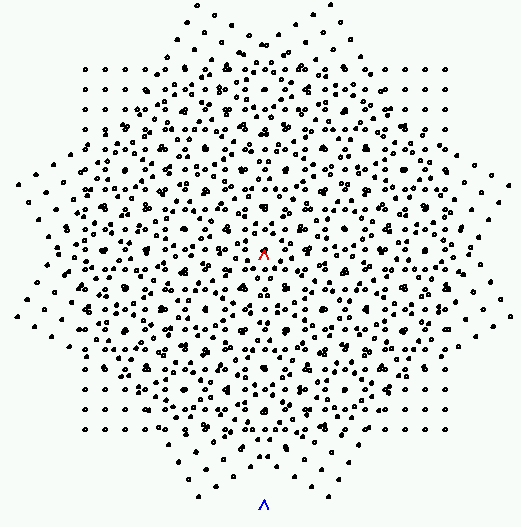
Problem 2 (Marroquin Pattern)
The Marroquin pattern of order n is formed by superimposing three square arrays of points of size 2n + 1. Consequently, each array has an odd number of rows and columns. The arrays are rotated about the center (i.e., n + 1) point. The orientations of the arrays (relative to the x-axis) are 0, 60, and 120 degrees. You will write a function called marroquin which takes a single integer argument, n, and returns the Marroquin pattern of order n. Example:
```
>(marroquin 9)
>#<struct:graphic>
```

Problem 3 (Tail-Recursive Spiral)

The following program draws a spiral:

(define spiral
  (lambda (angle len n)
    (if (= n 0)
        (adjoin)
        (adjoin (bend angle)
                (straight len)
                (spiral angle (add1 len) (sub1 n))))))

Rewrite spiral so that it is tail-recursive. You are free to use any helper functions you may require.

Problem 4 (S-expression Tree)
Write a Scheme program which, given an s-expression, draws the corresponding tree. Hint: This is a typical tree-recursion on pairs, i.e., the same recursion on car and cdr. You might find a function similiar to the following helpful for assembling the tree:
```
(define tree-step
  (lambda (trunk left-branch right-branch)
    (adjoin trunk
            (adorn (adjoin (bend -20) left-branch)
	           (adjoin (bend 20) right-branch)))))
```
Use the plumbing graphics function, text, to label the leaves of the tree.
Problem 5 (Fractal Curve)
Write a Scheme program which draws either the Gosper-Peano Curve (more challenging) or the Sierpinski Arrowhead (less challenging). To get full credit for Problem 5 (i.e., to get an A) you should do the Gosper-Peano Curve. The generators for these curves can be found on p. 70 and p. 142 (respectively) of Benoit Mandelbrot's The Fractal Geometry of Nature.

What You Should Hand In

Listings of all your code.
Representative graphic output.

When You Should Hand It In

The above should be handed in at the beginning of class on Mon. Oct 16.

* This webpage is located at http://cs.unm.edu/~williams/cs257/project1f00.html

CS 257 (Fall 2000) Project 1: E. coli we hardly knew ye. *

Problem 1 (Bacterial Chemotaxis)

Problem 2 (Marroquin Pattern)

Problem 3 (Tail-Recursive Spiral)

Problem 4 (S-expression Tree)

Problem 5 (Fractal Curve)

What You Should Hand In

When You Should Hand It In