CS 432.1 Project 3: Digital Watermarking *
In this project you are going to experiment with a technique for
hiding information in an image known as digital watermarking.
Digital watermarks can encode many different kinds of information in
an image yet remain invisible. The most obvious application is to use
watermarks to encode information which can prove ownership, e.g.,
copyrights. However, digital watermarks can also be used to encode
copy or read permissions, time stamps and quality control
information. They can be used to encode latitude, longitude, altitude
and sensor characteristics in images collected by satellite. Finally,
they can be used to encode content tags useful for addressing image
database queries or indications of whether or not an image is suitable
for viewing by children.
While a caption can become detached from an image, a watermark cannot
be. To prevent a watermark from being removed (either intentionally
or unintentionally) it should be robust to those operations commonly
performed on images. These include 1) cropping and undersampling; 2)
encoding and decoding operations used in image compression (e.g.,
JPEG); 3) geometric and point operations (e.g., rotation and histogram
equalization) and 4) re-watermarking.
Technical Background
We are going to experiment with a simple technique which uses a
symmetrical watermark to modulate the amplitudes of an image's
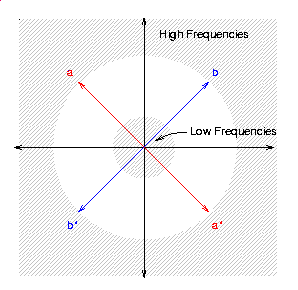
frequency spectrum. Recall that the Fourier transform of a real-valued
function possesses Hermite symmetry. That is, f(x,y)=f*(-x,-y),
where the "*" indicates the complex conjugate (see figure below). The
watermark must possess the same symmetry---the use of a
non-symmetrical transfer function would create imaginary components in
the watermarked image. The watermark is constructed by summing
reflected copies of a natural image of one quarter size and
normalizing the grey levels of the resulting image to a tiny sub-range
centered on unity (i.e., one plus/minus some epsilon). Because the
transfer function is real-valued, this changes only the amplitudes
(and not the phases) of the Fourier transform coefficients.
Consequently, it allows a significant amount of energy to be inserted
into the image without creating visible image artifacts.
As an example, we can take an image of Microsoft chairman Bill Gates
(after the notorious Belgium pie throwing incident) of size 127 x 127
and use it to construct a watermark for a 256 x 256 image of Leonardo
da Vinci's Mona Lisa.**
Step 1:  Step 2:
Step 2: 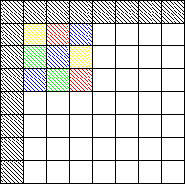 Step 3:
Step 3: 
Note: Grey pixels in the above figure represent 1's.

Note that this watermark possesses four-fold symmetry and that this is
more symmetry than is (strictly speaking) necessary. To see an example
of a watermark possessing the minimum symmetry necessary, click here. Note also the extra initial row and
column. This is to match the format used by Khoros to store the
discrete Fourier transform in memory. Representing the fourier
transform in memory so that it is symmetric about a single pixel (the
zeroth frequency), requires an odd number of rows and columns. However
(due to the nature of the FFT), it is computationally expedient to
compute fourier transforms for images with size equal to integral
powers of two. Clearly, such images always have an even number of rows
and columns. Hence, the extra row and column.
The following images show the Mona Lisa and its Fourier transform.


The following images show the Fourier transform after it has been
multiplied by the Bill Gates watermark. Because the watermark image
is very nearly one everywhere, there is no visible change. The
watermarked Mona Lisa image is then computed by inverse Fourier
Transform. The watermark is invisible.


To extract the watermark, we divide the Fourier transform of the
watermarked image by the Fourier transform of the original image.
This division produces the watermark which was previously inserted.
The watermark extracted from the Mona Lisa image is shown below:

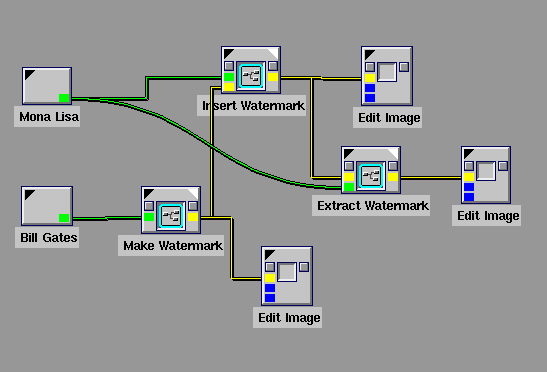
Project Outline
In this project, you will use Cantata to build three
encapsulated workspaces called Make Watermark, Insert
Watermark, and Extract Watermark:***
- Make Watermark---Inputs an image (of unspecified size and
type) to be used to generate the watermark together with a value for
epsilon and outputs a watermark image of size 256 x 256 and type
DOUBLE. You are free to use either of the two generation schemes
outlined above (or a scheme of your own invention) to create the
necessary symmetry in your watermark.
- Insert Watermark---Inputs an image of size 256 x 256 (of
unspecified type) to be watermarked together with the watermark
generated by Make Watermark and outputs a watermarked image of
type DOUBLE.
- Extract Watermark---Inputs a watermarked image generated
by Insert Watermark together with an unwatermarked image of size
256 x 256 (of unspecified type) and outputs the extracted watermark.
A Cantata workspace showing the three glyphs as they would be
typically used is shown below.
After implementing the three encapsulated workspaces described above,
you will experiment with the watermarking system to determine the best
value for the epsilon parameter. To do this, you need to bound the
parameter from above and below. To bound it from above, you need to
find the largest value of epsilon (i.e., epsilon_max) which
does not introduce "unnacceptable" visible artifacts into the
image. [Note: Clearly, "unnacceptable" is a somewhat subjective
notion. All that is required is that you use common sense and be
prepared to defend your choice.] A binary search is probably the best
systematic procedure for doing this.
To bound the parameter from below, you need to find the smallest value
of epsilson (i.e., epsilon_min) which will allow the watermark to
survive (in detectable form) the various image processing operations
which you will subject it to. These include:
- Cropping -- You will demonstrate that the watermark is
still detectable in a subregion of size 128 x 128. [Note:
To see how this is done, click here. ]
- Undersampling -- You will demonstrate that the watermark is
still detectable after you reduce the size of the
image by a factor of two.
- Rotation -- You will demonstrate that the watermark is
still detectable after you have rotated the image by 45 degrees.
- JPEG Encoding -- You will demonstrate that the watermark
is still detectable after it has been encoded into JPEG with image
quality set to 75%.
At this point, you may find that epsilon_min >
epsilon_max. This indicates that there is no acceptable value for
epsilon which will work for your choice of image and watermark. If
you believe that this is the case, just say so. There is no "right"
answer. However, be prepared to defend your conclusion(s). It may be
that a little bit more experimentation (effort) will allow you to
recover the watermark in a recognizable (albeit highly degraded) form.
This is all that is necessary. It doesn't have to be pretty.
Hints
- You are likely to find that Flip, Pad, Extract and
Inset are useful for creating your watermark.
- When possible, the key to recovering the watermark from a
transformed image is to invert the transformation.
- You can use xv to encode/decode your image into/from JPEG.
- Real and Imaginary allow you to extract the real
or imaginary parts of a complex image.
- Rather than display a complex image with Edit Image it is
best to display only the real part.
- Histogram equalization is very useful for improving the contrast
of degraded and nearly invisible watermarks.
What You Should Hand In
You should hand in a concise (less than 8 page) research report
describing your project. This report should include a description of
the process you used to bound epsilon from above and a discussion of
the criterion you used to judge image quality. It should also include
short descriptions of the methods you used to recover the watermark
after cropping, undersampling, rotation and JPEG encoding. The
following should be included either in the body of the report (where
appropriate) or in an appendix:
- Screen dumps showing the component glyphs and links of each of
the three encapsulated workspaces, Make Watermark Insert
Watermark and Extract Watermark.
- Hardcopy of an unwatermarked size 256 x 256 test image of your choice.
- Hardcopy of the image which you used to create your watermark.
- Hardcopy of your watermark.
- Hardcopy of the test image watermarked at epsilon =
(epsilon_min + epsilon_max)/2.
- Histogram of the imaginary part of the watermarked test image together
with the maximum and minimum imaginary value.
- Hardcopy of the 128 x 128 subregion and recovered watermark.
- Hardcopy of the undersampled image and recovered watermark.
- Hardcopy of the rotated image and recovered watermark.
- Hardcopy of the JPEG encoded image and recovered watermark.
When You Should Hand It In
The above should be handed in at the beginning of class, Fri. April 9.
Of Possible Interest
* This webpage is located at http://cs.unm.edu/~williams/cs432/project3s99.html
** These examples are in honor of Gates' multi-million dollar purchase
of the Codex Leicester, da Vinci's treatise on fluids in
motion.
*** The glyphs for encapsulated workspaces can be used in Cantata just
like those of kroutines and xvroutines. The first chapter of the
Cantata Visual Programming Manual includes detailed instructions
for creating encapsulated workspaces.


 Step 2:
Step 2:  Step 3:
Step 3: 






