September 09, 2011
What is the probability of a 9/11-size terrorist attack?
Sunday is the 10-year anniversary of the 9/11 terrorist attacks. As a commemoration of the day, I'm going to investigate answers to a very simple question: what is the probability of a 9/11-size or larger terrorist attack?
There are many ways we could try to answer this question. Most of them don't involve using data, math and computers (my favorite tools), so we will ignore those. Even using quantitative tools, approaches differ based on how strong are the assumptions they make about the social and political processes that generate terrorist attacks. We'll come back to this point throughout the analysis.
Before doing anything new, it's worth repeating something old. For the better part of the past 8 years that I've been studying the large-scale patterns and dynamics of global terrorism (see for instance, here and here), I've emphasized the importance of taking an objective approach to the topic. Terrorist attacks may seem inherently random or capricious or even strategic, but the empirical evidence demonstrates that there are patterns and that these patterns can be understood scientifically. Earthquakes and seismology serves as an illustrative example. Earthquakes are extremely difficult to predict, that is, to say beforehand when, where and how big they will be. And yet, plate tectonics and geophysics tells us a great deal about where and why they happen and the famous Gutenberg-Richter law tells us roughly how often quakes of different sizes occur. That is, we're quite good at estimating the long-time frequencies of earthquakes because larger scales allows us to leverage a lot of empirical and geological data. The cost is that we lose the ability to make specific statements about individual earthquakes, but the advantage is insight into the fundamental patterns and processes.
The same can be done for terrorism. There's now a rich and extensive modern record of terrorist attacks worldwide [1], and there's no reason we can't mine this data for interesting observations about global patterns in the frequencies and severities of terrorist attacks. This is where I started back in 2003 and 2004, when Maxwell Young and I started digging around in global terrorism data. Catastrophic events like 9/11, which (officially) killed 2749 people in New York City, might seem so utterly unique that they must be one-off events. In their particulars, this is almost surely true. But, when we look at how often events of different sizes (number of fatalities) occur in the historical record of 13,407 deadly events worldwide [2], we see something remarkable: their relative frequencies follow a very simple pattern.

The figure shows the fraction of events that killed at least x individuals, where I've divided them into "severe" attacks (10 or more fatalities) and "normal" attacks (less than 10 fatalities). The lions share (92.4%) of these events are of the "normal" type, killing less than 10 individuals, but 7.6% are "severe", killing 10 or more. Long-time readers have likely heard this story before and know where it's going. The solid line on the figure shows the best-fitting power-law distribution for these data [3]. What's remarkable is that 9/11 is very close to the curve, suggesting that statistically speaking, it is not an outlier at all.
A first estimate: In 2009, the Department of Defense received the results of a commissioned report on "rare events", with a particular emphasis on large terrorist attacks. In section 3, the report walks us through a simple calculation of the probability of a 9/11-sized attack or larger, based on my power-law model. It concludes that there was a 23% chance of an event that killed 2749 or more between 1968 and 2006. [4] The most notable thing about this calculation is that its magnitude makes it clear that 9/11 should not be considered a statistical outlier on the basis of its severity.
How we can we do better: Although probably in the right ballpark, the DoD estimate makes several strong assumptions. First, it assumes that the power-law model holds over the entire range of severities (that is x>0). Second, it assumes that the model I published in 2005 is perfectly accurate, meaning both the parameter estimates and the functional form. Third, it assumes that events are generated independently by a stationary process, meaning that the production rate of events over time has not changed nor has the underlying social or political processes that determine the frequency or severity of events. We can improve our estimates by improving on these assumptions.
A second estimate: The first assumption is the easiest to fix. Empirically, 7.6% of events are "severe", killing at least 10 people. But, the power-law model assumed by the DoD report predicts that only 4.2% of events are severe. This means that the DoD model is underestimating the probability of a 9/11-sized event, that is, the 23% estimate is too low. We can correct this difference by using a piecewise model: with probability 0.076 we generate a "severe" event whose size is given by a power-law that starts at x=10; otherwise we generate a "normal" event by choosing a severity from the empirical distribution for 0 < x < 10 . [5] Walking through the same calculations as before, this yields an improved estimate of a 32.6% chance of a 9/11-sized or larger event between 1968-2008.
A third estimate: The second assumption is also not hard to improve on. Because our power-law model is estimated from finite empirical data, we cannot know the alpha parameter perfectly. Our uncertainty in alpha should propagate through to our estimate of the probability of catastrophic events. A simple way to capture this uncertainty is to use a computational bootstrap resampling procedure to generate many synthetic data sets like our empirical one. Estimating the alpha parameter for each of these yields an ensemble of models that represents our uncertainty in the model specification that comes from the empirical data.
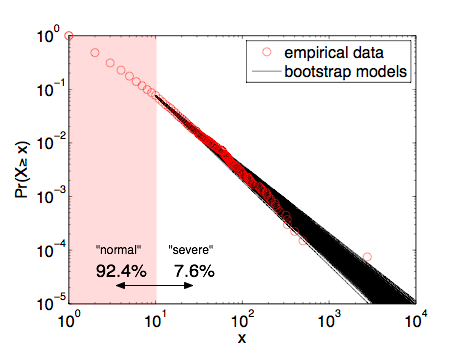
This figure overlays 1000 of these bootstrap models, showing that they do make slightly different estimates of the probability of 9/11-sized events or larger. As a sanity check, we find that the mean of these bootstrap parameters is alpha=2.397 with a standard deviation of 0.043 (quite close to the 2.4+/-0.1 value I published in 2009 [6]). Continuing with the simulation approach, we can numerically estimate the probability of a 9/11-sized or larger event by drawing synthetic data sets from the models in the ensemble and then asking what fraction of those events are 9/11-sized or larger. Using 10,000 repetitions yields an improved estimate of 40.3%.
Some perspective: Having now gone through three calculations, it's notable that the probability of a 9/11-sized or larger event has almost doubled as we've improved our estimates. There are still additional improvements we could do, however, and these might push the number back down. For instance, although the power-law model is a statistically plausible model of the frequency-severity data, it's not the only such model. Alternatives like the stretched exponential or the log-normal decay faster than the power law, and if we were to add them to the ensemble of models in our simulation, they would likely yield 9/11-sized or larger events with lower frequencies and thus likely pull the probability estimate down somewhat. [7]
Peering into the future: Showing that catastrophic terrorist attacks like 9/11 are not in fact statistical outliers given the sheer magnitude and diversity of terrorist attacks worldwide over the past 40 years is all well and good, you say. But, what about the future? In principle, these same models could be easily used to make such an estimate. The critical piece of information for doing so, however, is a clear estimate of the trend in the number of events each year. The larger that number, the greater the risk under these models of severe events. That is, under a fixed model like this, the probability of catastrophic events is directly related to the overall level of terrorism worldwide. Let's look at the data.
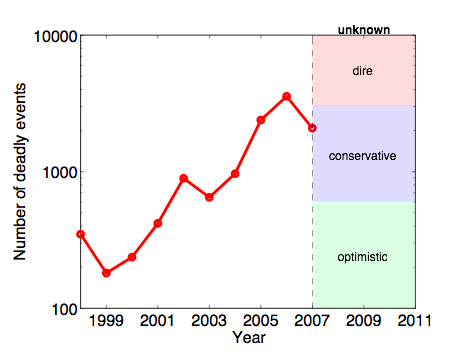
Do you see a trend here? It's difficult to say, especially with the changing nature of the conflicts in Iraq and Afghanistan, where many of the terrorist attacks of the past 8 years have been concentrated. It seems unlikely, however, that we will return to the 2001 levels (200-400 events per year; the optimist's scenario). A dire forecast would have the level continue to increase toward a scary 10,000 events per year. A more conservative forecast, however, would have the rate continue as-is relative to 2007 (the last full year for which I have data), or maybe even decrease to roughly 1000 events per year. Using our estimates from above, 1000 events overall would generate about 75 "severe" events (more than 10 fatalities) per year. Plugging this number into our computational model above (third estimate approach), we get an estimate of roughly a 3% chance of a 9/11-sized or larger attack each year, or about a 30% chance over the next decade. Not a certainty by any means, but significantly greater than is comfortable. Notably, this probability is in the same ballpark for our estimates for the past 40 years, which goes to show that the overall level of terrorism worldwide has increased dramatically during those decades.
It bears repeating that this forecast is only as good as the models on which it is based, and there are many things we still don't know about the underlying social and political processes that generate events at the global scale. (In contrast to the models the National Hurricane Center uses to make hurricane track forecasts.) Our estimates for terrorism all assume a homogeneous and stationary process where event severities are independent random variables, but we would be foolish to believe that these assumptions are true in the strong sense. Technology, culture, international relations, democratic movements, urban planning, national security, etc. are all poorly understood and highly non-stationary processes that could change the underlying dynamics in the future, making our historical models less reliable than we would like. So, take these estimates for what they are, calculations and computations using reasonable but potentially wrong assumptions based on the best historical data and statistical models currently available. In that sense, it's remarkable that these models do as well as they do in making fairly accurate long-term probabilistic estimates, and it seems entirely reasonable to believe that better estimates can be had with better, more detailed models and data.
Update 9 Sept. 2011: In related news, there's a piece in the Boston Globe (free registration required) about the impact 9/11 had on what questions scientists investigate that discusses some of my work.
-----
[1] Estimates differ between databases, but the number of domestic or international terrorist attacks worldwide between 1968 and 2011 is somewhere in the vicinity of 50,000-100,000.
[2] The historical record here is my copy of the National Memorial Institute for the Prevention of Terrorism (MIPT) Terrorism Knowledge Base, which stores detailed information on 36,018 terrorist attacks worldwide from 1968 to 2008. Sadly, the Department of Homeland Security pulled the plug on the MIPT data collection effort a few years ago. The best remaining data collection effort is the one run by the University of Maryland's National Consortium for the Study of Terrorism and Response to Terrorism (START) program.
[3] For newer readers: a power-law distribution is a funny kind of probability distribution function. Power laws pop up all over the place in complex social and biological systems. If you'd like an example of how weird power-law distributed quantities can be, I highly recommend Clive Crook's 2006 piece in The Atlantic title "The Height of Inequality" in which he considers what the world would look like if human height were distributed as unequally as human wealth (a quantity that is very roughly power-law-like).
[4] If you're curious, here's how they did it. First, they took the power-law model and the parameter value I estimated (alpha=2.38) and computed the model's complementary cumulative distribution function. The "ccdf" tells you the probability of observing an event at least as large as x, for any choice of x. Plugging in x=2749 yields p=0.0000282. This gives the probability of any single event being 9/11-sized or larger. The report was using an older, smaller data set with N=9101 deadly events worldwide. The expected number of these events 9/11-sized or larger is then p*N=0.257. Finally, if events are independent then the probability that we observe at least one event 9/11-sized or larger in N trials is 1-exp(-p*N)=0.226. Thus, about a 23% chance.
[5] This changes the calculations only slightly. Using alpha=2.4 (the estimate I published in 2009), given that a "severe" event happens, the probability that it is at least as large as 9/11 is p=0.00038473 and there were only N=1024 of them from 1968-2008. Note that the probability is about a factor of 10 larger than the DoD estimate while the number of "severe" events is about a factor of 10 smaller, which implies that we should get a probability estimate close to theirs.
[6] In "Power-law distributions in empirical data," SIAM Review 51(4), 661-703 (2009), with Cosma Shalizi and Mark Newman.
[7] This improvement is mildly non-trivial, so perhaps too much effort for an already long-winded blog entry.
posted September 9, 2011 02:17 PM in Terrorism | permalink | Comments (1)
December 14, 2010
Statistical Analysis of Terrorism
Yesterday, my work on global statistical patterns in terrorism [1] was featured in a long article in the magazine Miller-McCune called The Physics of Terrorism, written by Michael Haederle [2].
Much of the article focuses on the weird empirical fact that the frequency of severe terrorist attacks is well described by a power-law distribution [3,4], although it also discusses my work on robust patterns of behavior in terrorist groups, for instance, showing that they typically increase the frequency of their attacks as they get older (and bigger and more experienced), and moreover that they do it in a highly predictable way. There are several points I like most about Michael's article. First, he emphasizes that these patterns are not just nice statistical descriptions of things we already know, but rather they show that some things we thought were fundamentally different and unpredictable are actually related and that we can learn something about large but rare events by studying the more common smaller events. And second, he emphasizes the fact that these patterns can actually be used to make quantitative, model-based statistical forecasts about the future, something current methods in counter-terrorism struggle with.
Of course, there's a tremendous amount of hard-nosed scientific work that remains to be done to develop these empirical observations into practical tools, and I think it's important to recognize that they will not be a silver bullet for counter-terrorism, but they do show us that much more can be done here than has been traditionally believed and that there are potentially fundamental constraints on terrorism that could serve as leverage points if exploited appropriately. That is, so to speak, there's a forest out there that we've been missing by focusing only on the trees, and that thinking about forests as a whole can in fact help us understand some things about the behavior of trees. I don't think studying large-scale statistical patterns in terrorism or other kinds of human conflict takes away from the important work of studying individual conflicts, but I do think it adds quite a bit to our understanding overall, especially if we want to think about the long-term. How does that saying go again? Oh right, "those who do not learn from history are doomed to repeat it" (George Santayana, 1863-1952) [5].
The Miller-McCune article is fairly long, but here are a few good excerpts that capture the points pretty well:
Last summer, physicist Aaron Clauset was telling a group of undergraduates who were touring the Santa Fe Institute about the unexpected mathematical symmetries he had found while studying global terrorist attacks over the past four decades. Their professor made a comment that brought Clauset up short. "He was surprised that I could think about such a morbid topic in such a dry, scientific way," Clauset recalls. "And I hadn’t even thought about that. It was just … I think in some ways, in order to do this, you have to separate yourself from the emotional aspects of it."
But it is his terrorism research that seems to be getting Clauset the most attention these days. He is one of a handful of U.S. and European scientists searching for universal patterns hidden in human conflicts — patterns that might one day allow them to predict long-term threats. Rather than study historical grievances, violent ideologies and social networks the way most counterterrorism researchers do, Clauset and his colleagues disregard the unique traits of terrorist groups and focus entirely on outcomes — the violence they commit.
“When you start averaging over the differences, you see there are patterns in the way terrorists’ campaigns progress and the frequency and severity of the attacks,” he says. “This gives you hope that terrorism is understandable from a scientific perspective.” The research is no mere academic exercise. Clauset hopes, for example, that his work will enable predictions of when terrorists might get their hands on a nuclear, biological or chemical weapon — and when they might use it.
It is a bird’s-eye view, a strategic vision — a bit blurry in its details — rather than a tactical one. As legions of counterinsurgency analysts and operatives are trying, 24-style, to avert the next strike by al-Qaeda or the Taliban, Clauset’s method is unlikely to predict exactly where or when an attack might occur. Instead, he deals in probabilities that unfold over months, years and decades — probability calculations that nevertheless could help government agencies make crucial decisions about how to allocate resources to prevent big attacks or deal with their fallout.
-----
[1] Here are the relevant scientific papers:
On the Frequency of Severe Terrorist Attacks, by A. Clauset, M. Young and K. S. Gledistch. Journal of Conflict Resolution 51(1), 58 - 88 (2007).
Power-law distributions in empirical data, by A. Clauset, C. R. Shalizi and M. E. J. Newman. SIAM Review 51(4), 661-703 (2009).
A generalized aggregation-disintegration model for the frequency of severe terrorist attacks, by A. Clauset and F. W. Wiegel. Journal of Conflict Resolution 54(1), 179-197 (2010).
The Strategic Calculus of Terrorism: Substitution and Competition in the Israel-Palestine Conflict, by A. Clauset, L. Heger, M. Young and K. S. Gleditsch Cooperation & Conflict 45(1), 6-33 (2010).
The developmental dynamics of terrorist organizations, by A. Clauset and K. S. Gleditsch. arxiv:0906.3287 (2009).
A novel explanation of the power-law form of the frequency of severe terrorist events: Reply to Saperstein, by A. Clauset, M. Young and K.S. Gleditsch. Forthcoming in Peace Economics, Peace Science and Public Policy.
[2] It was also slashdotted.
[3] If you're unfamiliar with power-law distributions, here's a brief explanation of how they're weird, taken from my 2010 article in JCR:
What distinguishes a power-law distribution from the more familiar Normal distribution is its heavy tail. That is, in a power law, there is a non-trivial amount of weight far from the distribution's center. This feature, in turn, implies that events orders of magnitude larger (or smaller) than the mean are relatively common. The latter point is particularly true when compared to a Normal distribution, where there is essentially no weight far from the mean.
Although there are many distributions that exhibit heavy tails, the power law is special and exhibits a straight line with slope alpha on doubly-logarithmic axes. (Note that some data being straight on log-log axes is a necessary, but not a sufficient condition of being power-law distributed.)
Power-law distributed quantities are not uncommon, and many characterize the distribution of familiar quantities. For instance, consider the populations of the 600 largest cities in the United States (from the 2000 Census). Among these, the average population is only x-bar =165,719, and metropolises like New York City and Los Angles seem to be "outliers" relative to this size. One clue that city sizes are not well explained by a Normal distribution is that the sample standard deviation sigma = 410,730 is significantly larger than the sample mean. Indeed, if we modeled the data in this way, we would expect to see 1.8 times fewer cities at least as large as Albuquerque (population 448,607) than we actually do. Further, because it is more than a dozen standard deviations above the mean, we would never expect to see a city as large as New York City (population 8,008,278), and largest we expect would be Indianapolis (population 781,870).
As a more whimsical second example, consider a world where the heights of Americans were distributed as a power law, with approximately the same average as the true distribution (which is convincingly Normal when certain exogenous factors are controlled). In this case, we would expect nearly 60,000 individuals to be as tall as the tallest adult male on record, at 2.72 meters. Further, we would expect ridiculous facts such as 10,000 individuals being as tall as an adult male giraffe, one individual as tall as the Empire State Building (381 meters), and 180 million diminutive individuals standing a mere 17 cm tall. In fact, this same analogy was recently used to describe the counter-intuitive nature of the extreme inequality in the wealth distribution in the United States, whose upper tail is often said to follow a power law.
Although much more can be said about power laws, we hope that the curious reader takes away a few basic facts from this brief introduction. First, heavy-tailed distributions do not conform to our expectations of a linear, or normally distributed, world. As such, the average value of a power law is not representative of the entire distribution, and events orders of magnitude larger than the mean are, in fact, relatively common. Second, the scaling property of power laws implies that, at least statistically, there is no qualitative difference between small, medium and extremely large events, as they are all succinctly described by a very simple statistical relationship.
[4] In some circles, power-law distributions have a bad reputation, which is not entirely undeserved given the way some scientists have claimed to find them everywhere they look. In this case, though, the data really do seem to follow a power-law distribution, even when you do the statistics properly. That is, the power-law claim is not just a crude approximation, but a bona fide and precise hypothesis that passes a fairly harsh statistical test.
[5] Also quoted as "Those who cannot remember the past are condemned to repeat their mistakes".
posted December 14, 2010 10:39 AM in Scientifically Speaking | permalink | Comments (6)
June 11, 2010
The Future of Terrorism
Attention conservation notice: This post mainly concerns an upcoming Public Lecture I'm giving in Santa Fe NM, as part of the Santa Fe Institute's annual lecture series.
Wednesday, June 16, 2010, 7:30 PM at the James A. Little Theater
Nearly 200 people died in the Oklahoma City bombing of 1995, over 200 died in the 2002 nightclub fire in Bali, and at least 2700 died in the 9/11 attacks on the World Trade Center Towers. Such devastating events captivate and terrify us mainly because they seem random and senseless. This kind of unfocused fear is precisely terrorism's purpose. But, like natural disasters, terrorism is not inexplicable: it follows patterns, it can be understood, and in some ways it can be forecasted. Clauset explores what a scientific approach can teach us about the future of modern terrorism by studying its patterns and trends over the past 50 years. He reveals surprising regularities that can help us understand the likelihood of future attacks, the differences between secular and religious terrorism, how terrorist groups live and die, and whether terrorism overall is getting worse.
Naturally, this will be my particular take on the topic, driven in part by my own research on patterns and trends in terrorism. There are many other perspectives, however. For instance, from the US Department of Homeland Security (from 2007), the US Department of Justice (from 2009) and the French Institute for International Relations (from 2006). Perhaps the main difference between these and mine is in my focus on taking a data- and model-driven approach to understanding the topic, and on emphasizing terrorism worldwide rather than individual conflicts or groups.
Update 13 July 2010: The video of my lecture is now online. The running time is about 80 minutes; the talk lasted about 55 and I spent the rest of the time taking questions from the audience.
posted June 11, 2010 08:49 PM in Terrorism | permalink | Comments (0)
January 25, 2010
On the frequency of severe terrorist attacks; redux
Sticking with the theme of terrorism, in the new issue of the Journal of Conflict Resolution is an article by Frits Wiegel and me [1], in which we analyze, generalize, and discuss the Johnson et al. model on the internal dynamics of terrorist / insurgent groups [2].
The goal of the paper was to (i) relax one of the mathematical assumptions Johnson et al. initially made when they introduced the model back in 2005, (ii) clearly articulate its assumptions and discuss the evidence for and against them, (iii) discuss the relevance of the model for counter-terrorism / counter-insurgency policies, and (iv) identify ways the model's assumptions and predictions could be tested using empirical data.
Here's the abstract:
We present and analyze a model of the frequency of severe terrorist attacks, which generalizes the recently proposed model of Johnson et al. This model, which is based on the notion of self-organized criticality and which describes how terrorist cells might aggregate and disintegrate over time, predicts that the distribution of attack severities should follow a power-law form with an exponent of alpha=5/2. This prediction is in good agreement with current empirical estimates for terrorist attacks worldwide, which give alpha=2.4 \pm 0.2, and which we show is independent of certain details of the model. We close by discussing the utility of this model for understanding terrorism and the behavior of terrorist organizations, and mention several productive ways it could be extended mathematically or tested empirically.
Looking forward, this paper is really just a teaser. There's still a tremendous amount of work left to do both in terms of identifying other robust patterns in global terrorism and in terms of explaining where those patterns come from. The hardest part of this line of research promises to be reconciling traditional economics-style assumptions in conflict research (that terrorists are perfectly rational actors: their actions are highly strategic, are best explained using game theory, and are otherwise contingent on the particular local history and politics) with these newer physics-style assumptions (that terrorists are highly irrational "dumb" actors: their actions blindly follow fundamental "laws", are best explained using simple mechanical models, and are otherwise random). The truth is almost surely a compromise between these two extremes, one that includes both local strategic flexibility and contingency, along with fundamental constraints created by the "physics" of planning and carrying out terrorist attacks. Developing a theory that captures the right amount of both approaches seems hard, but exciting.
-----
[1] A. Clauset and F. W. Wiegel. "A generalized aggregation-disintegration model for the frequency of severe terrorist attacks." Journal of Conflict Resolution 54(1): 179-197 (2010). (arxiv version)
[2] This model should now perhaps be called the Bohorquez et al. model, since that's the author order for their published version, which appeared last month in Nature. See also the accompanying commentary in Nature, in which I'm quoted.
posted January 25, 2010 03:18 PM in Terrorism | permalink | Comments (4)
January 12, 2010
The future of terrorism
Here's one more thing. SFI invited me to give a public lecture as part of their 2010 lecture series. These talks are open to, and intended for, the public. They're done once a month, in Santa Fe NM over most of the year. This year, the schedule is pretty impressive. For instance, on March 16, Daniel Dennett will be giving a talk about the evolution of religion.
My own lecture, which I hope will be good, will be on June 16th:
One hundred sixty-eight people died in the Oklahoma City bombing of 1995, 202 people died in the 2002 nightclub fire in Bali, and at least 2749 people died in the 9/11 attacks on the World Trade Center Towers. Such devastating events captivate and terrify us mainly because they seem random and senseless. This kind of unfocused fear is precisely terrorism's purpose. But, like natural disasters, terrorism is not inexplicable: it follows patterns, it can be understood, and in some ways it can be forecasted. Clauset explores what a scientific approach can teach us about the future of modern terrorism by studying its patterns and trends over the past 50 years. He reveals surprising regularities that can help us understand the likelihood of future attacks, the differences between secular and religious terrorism, how terrorist groups live and die, and whether terrorism overall is getting worse.
Also, if you're interested in my work on terrorism, there's now a video online of a talk I gave on their group dynamics last summer in Zurich.
posted January 12, 2010 10:53 AM in Self Referential | permalink | Comments (2)
September 12, 2007
Is terrorism getting worse? A look at the data. (part 2)
Cosma and Matt both wanted to see how the trend fares when we normalize by the increase in world popluation, i.e., has terrorism worsened per capita. Pulling data from the US Census's world population database, we can do this. The basic facts are that the world's population has increased at a near constant rate over the past 40 years, going from about 3.5 billion in 1968 to about 6.6 billion in 2007. In contrast, the total number of deaths per year from terrorism (according to MIPT) has gone from 115 (on average) over the first 10 years (1968 - 1977), to about 3900 (on average) over the last 10 years (1998 - 2007). Clearly, population increase alone (about a factor of 2) cannot explain the increase in total deaths per year (about a factor of 34).
However, this view gives a slightly misleading picture because the MIPT changed the way it tracked terrorism in 1998 to include domestic attacks worldwide. Previously, it only tracked transnational terrorism (target and attackers from different countries), so part of the the apparent large increase in deaths from terrorism in the past 10 years is due to simply including a greater range of events in the database. Looking at the average severity of an event circumvents this problem to some degree, so long as we assume there's no fundamental difference in the severity of domestic and transnational terrorism (fortunately, the distributions pre-1998 and post-1998 are quite similar, so this may be a reasonable assumption).
The misleading per capita figure is immediately below. One way to get at the question, however, is to throw out the past 10 years of data (domestic+transnational) and focus only on the first 30 years of data (transnational only). Here, the total number of deaths increased from the 115 (on average) in the first decade to 368 in the third decade (1988-1997), while the population increased from 3.5 billion in 1968 to 5.8 billion in 1997. The implication being that total deaths from transnational terrorism have increased more quickly than we would expect based on population increases, even if we account for the slight increase in lethality of attacks over this period. Thus, we can argue that the frequency of attacks has significantly increased in time.
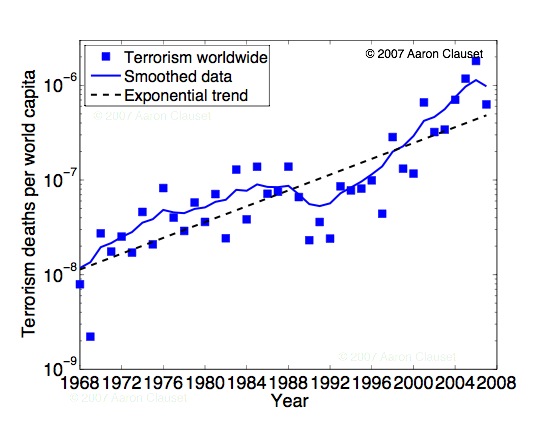
The more clear per capita-event figure is the next one. What's remarkable is that the per capita-event severity is extremely stable over the past 40 years, at about 1 death per billion (dpb) per event. This suggests that, if there really has been a large increase in the total deaths (per capita) from terrorism each year (as we argued above), then it must be mainly attributable to an increase in the number of lethal attacks each year, rather than attacks themselves becoming worse.
So, is terrorism getting worse? The answer is typically no, but that terrorism is becoming a more popular mode of behavior. From a policy point of view, this would seem a highly problematic trend.

A. Clauset, M. Young and K. S. Gledistch, "On the Frequency of Severe Terrorist Attacks." Journal of Conflict Resolution 51(1): 58 - 88 (2007).
posted September 12, 2007 08:12 AM in Political Wonk | permalink | Comments (2)
September 11, 2007
Is terrorism getting worse? A look at the data.
Data taken from the MIPT database and includes all events that list at least one death (10,936 events; 32.3% as of May 17, 2007). Scatter points are the average number of deaths for lethal attacks in a given year. Linear trend has a slope of roughly 1 additional death per 20 years, on average. (Obviously, a more informative characterization would be the distribution of deaths, which would give some sense of the variability about the average.) Smoothing was done using an exponential kernel, and black triangles indicate the years (1978, 1991 and 2006) of the local minima of the smoothed function. Other smoothing schemes give similar results, and the auto-correlation function on the scatter data indicates that the average severity of lethal attacks oscillates with a roughly 13 year periodicity. If this trend holds, note that 2006 was a low-point for lethal terrorism.
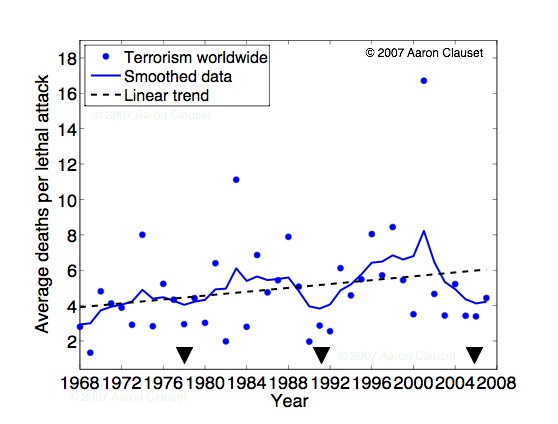
A. Clauset, M. Young and K. S. Gledistch, "On the Frequency of Severe Terrorist Attacks." Journal of Conflict Resolution 51(1): 58 - 88 (2007).
posted September 11, 2007 10:33 AM in Political Wonk | permalink | Comments (3)
July 26, 2005
Global patterns in terrorism; part III
Neil Johnson, a physicist at Lincoln College of Oxford University, with whom I've been corresponding about the mathematics of terrorism for several months, has recently put out a paper that considers the evolution of the conflicts in Iraq and Colombia. The paper (on arxiv, here) relies heavily on the work Maxwell Young and I did on the power law relationship between the frequency and severity of terrorist attacks worldwide.
Neil's article, much like our original one, has garnered some attention among the popular press, so far yielding an article at The Economist (July 21st) that also heavily references our previous work. I strongly suspect that there will be more, particularly considering the July 7th terrorist bombings in London, and Britain's continued conflicted relationship with its own involvement in the Iraq debacle.
Given the reasonably timely attention these analyses are garnering, the next obvious step in this kind of work is to make it more useful for policy-makers. What does it mean for law enforcement, for the United Nations, for forward-looking politicians that terrorism (and, if Neil is correct in his conjecture, the future of modern armed geopolitical conflict) has this stable mathematical structure? How should countries distribute their resources so as to minimize the fallout from the likely catastrophic terrorist attacks of the future? These are the questions that scientific papers typically stay as far from as possible - attempting to answer them takes one out of the scientific world and into the world of policy and politics (shark infested waters for sure). And yet, in order for this work to be relevant outside the world of intellectual edification, some sort of venture must be made.
posted July 26, 2005 12:57 AM in Scientifically Speaking | permalink | Comments (0)
February 21, 2005
Global patterns in terrorism; follow-up
Looks like my article with Maxwell Young is picking up some more steam. Phillip Ball, a science writer who often writes for the Nature Publishing Group, authored a very nice little piece which draws heavily on our results. You can read the piece itself here. It's listed under the "muse@nature" section, and I'm not quite sure what that means, but the article is nicely thought-provoking. Here's an excerpt from it:
And the power-law relationship implies that the biggest terrorist attacks are not 'outliers': one-off events somehow different from the all-too-familiar suicide bombings that kill or maim just a few people. Instead, it suggests that they are somehow driven by the same underlying mechanism.
Similar power-law relationships between size and frequency apply to other phenomena, such as earthquakes and fluctuations in economic markets. This indicates that even the biggest, most infrequent earthquakes are created by the same processes that produce hordes of tiny ones, and that occasional market crashes are generated by the same internal dynamics of the marketplace that produce daily wobbles in stock prices. Analogously, Clauset and Young's study implies some kind of 'global dynamics' of terrorism.
Moreover, a power-law suggests something about that mechanism. If every terrorist attack were instigated independently of every other, their size-frequency relationship should obey the 'gaussian' statistics seen in coin-tossing experiments. In gaussian statistics, very big fluctuations are extremely rare - you will hardly ever observe ten heads and ninety tails when you toss a coin 100 times. Processes governed by power-law statistics, in contrast, seem to be interdependent. This makes them far more prone to big events, which is why giant tsunamis and market crashes do happen within a typical lifetime. Does this mean that terrorist attacks are interdependent in the same way?
Here's a bunch of other places that have picked it up or are discussing it; the sites with original coverage about our research are listed first, while the rest are (mostly) just mirroring other sites:
(February 10) Physics Web (news site [original])
(February 18) Nature News (news site [original])
(March 2) World Science (news site [original])
(March 5) Watching America (news? (French) (Google cache) [original])
(March 5) Brookings Institute (think tank [original])
(March 19) Die Welt (one of the big three German daily newspapers (translation) [original] (in German))
3 Quarks Daily (blog, this is where friend Cosma Shalizi originally found the Nature pointer)
Science Forum (a lovely discussion)
The Anomalist (blog, Feb 18 news)
Science at ORF.at (news blog (in German))
Indymedia@UK (blog)
Wissenschaft-online (news (in German))
Economics Roundtable (blog)
Physics Forum (discussion)
Spektrum Direkt (news (in German))
Manila Times (Philippines news)
Rantburg (blog, good discussion in the comments)
Unknown (blog (in Korean))
Neutrino Unbound (reading list)
Discarded Lies (blog)
Global Guerrilas (nice blog by John Robb who references our work)
TheMIB (blog)
NewsTrove (news blog/archive)
The Green Man (blog, with some commentary)
Sapere (newspaper (in Italian)
Almanacco della Scienza (news? (in Italian))
Logical Meme (conservative blog)
Money Science (discussion forum (empty))
Always On (blog with discussion)
Citebase ePrint (citation information)
Crumb Trail (blog, thoughtful coverage)
LookSmart's Furl (news mirror?)
A Dog That Can Read Physics Papers (blog (in Japanese))
Tyranny Response Unit News (blog)
Chiasm Blog (blog)
Focosi Politics (blog?)
vsevcosmos LJ (blog)
larnin carves the blogck (blog (German?))
Brothers Judd (blog)
Gerbert (news? (French))
Dr. Frantisek Slanina (homepage, Czech)
Ryszard Benedykt (some sort of report/paper (Polish))
Mohammad Khorrami (translation of Physics Web story (Persian))
CyberTribe (blog)
Feedz.com (new blog)
The Daily Grail (blog)
Wills4223 (blog)
Mathematics Magazine
Physics Forum (message board)
CiteULike
Tempers Ball (message board)
A lot of these places reference each other. Seems like most of them are getting their information from either our arxiv posting, the PhysicsWeb story, or now the Nature story. I'll keep updating this list, as more places pick it up.
Update: It's a little depressing to me that the conservatives seem to be latching onto the doom-and-gloom elements of our paper as being justification for the ill-named War on Terrorism.
Update: A short while ago, we were contacted by a reporter for Die Welt, one of the three big German daily newspapers, who wanted to do a story on our research. If the story ever appears online, I'll post a link to it.
posted February 21, 2005 12:33 PM in Scientifically Speaking | permalink | Comments (1)
February 09, 2005
Global patterns in terrorism
 Although the severity of terrorist attacks may seem to be either random or highly planned in nature, it turns out that in the long-run, it is neither. By studying the set of all terrorist attacks worldwide between 1968 and 2004, we show that a simple mathematical rule, a power law with exponent close to two, governs the frequency and severity of attacks. Thus, if history is any basis to predict the future, we can predict with some confidence how long it will be before the next catastrophic attack will occur somewhere in the world.
Although the severity of terrorist attacks may seem to be either random or highly planned in nature, it turns out that in the long-run, it is neither. By studying the set of all terrorist attacks worldwide between 1968 and 2004, we show that a simple mathematical rule, a power law with exponent close to two, governs the frequency and severity of attacks. Thus, if history is any basis to predict the future, we can predict with some confidence how long it will be before the next catastrophic attack will occur somewhere in the world.
In joint work with Max Young, we've discovered the appearance of a surprising global pattern in terrorism over the past 37 years. The brief write up of our findings is on arXiv.org, and can be found here.
Update: PhysicsWeb has done a brief story covering this work as well. The story is fairly reasonable, although the writer omitted a statement I made about caution with respect to this kind of work. So, here it is:
Generally, one should be cautious when applying the tools of one field (e.g., physics) to make statements in another (e.g., political science) as in this case. The results here turned out to be quite nice, but in approaching similar questions in the future, we will continue to exercise that caution.
posted February 9, 2005 10:30 PM in Scientifically Speaking | permalink | Comments (2)
January 13, 2005
Terrorism: looking forward, looking back
This month's edition of The Atlantic has a pair of excellent articles which focus on terrorism and recent US policy about it. The first article, by former anti-terrorism chief Richard Clarke, is an imagined retrospective from the year 2011 on the decade that followed the declaration of the (ill-named) War on Terrorism. In it, he describes a nation which is only capable of reacting (poorly) to previously identified but largely ignored dangers of international terrorist strikes on US soil. Erring on the side of doom-sayer, Clarke paints a sobering yet compelling picture of how US domestic policy will slowly but surely reduce civil liberties and economic viability in favor of fortress-style security. The second, by long-time Atlantic correspondent James Fallows, describes in honest and uncomfortable detail the current head-in-the-sand security strategies being pursued by those in power. Drawing a strong analogy to the cautious and even-handed approach that Truman, Kennan and Marshall took toward preparing the nation for the long struggle with communism, Fallows points out that current policy is short-sighted and lopsided toward showy "feel good" measures that likely make civilian less secure than more. He closes with a discussion of the problem of "loose nukes" (primarily from Russia's poorly guarded and decaying stockpile, but also potentially from countries like Pakistan who have not signed the Nuclear Non-Proliferation Treaty), and the lack of seriousness coming from Washington with regard to addressing this imminently approachable goal. Indeed, in 2002 bin Laden issued a fatwa authorizing the killing of four million Americans with half of them being children in retribution for US Middle East policy - achieving this number can only be done with something like a nuclear bomb.
My reaction to these thoughtful and well-measured articles is that they basically nail the problem with US policy on terrorism exactly. The US has not been serious about facing the changes that need to be made (the "Department of Homeland Security" is basically misnomer), and anti-terrorism funding has become a massive source of pork for congressmen. Matched with the hypocritical rhetoric of the government, and the continued US insistence on an oil-economy, we're basically significantly worse off now than we were pre-September 11th. Stealing from the popular college student adage, our current domestic security policy is like masturbation: it feels good right now, but ultimately, we're only fucking ourselves.
Ten Years Later, by Richard Clarke
Victory Without Success, James Fallows
If these weren't scathing enough, the award winning William Langewiesche writes a Letter from Baghdad concerning the depth and pervasiveness of the insurgency there. Langewiesche describes the deteriorating (that word doesn't do his account justice - "anarchic" is more apt) security situation there as having reached the point that a continued US presence will indeed only intensify the now endemic guerrilla warfare. An interesting contrast is between the Iraqi resistance and, for instance, the French Resistance of World War II. I strongly suspect, that ultimately, the US does not have the stomach to truly break the resistance, as that would essentially require using the same draconian measures that Saddam used to install the Baathist regime. Depressing, indeed.
posted January 13, 2005 03:24 PM in Political Wonk | permalink | Comments (0)