Structure+Strangeness: Complex Systems Archives

September 06, 2012

Be an Omidyar Fellow at the Santa Fe Institute

The Santa Fe Institute is hiring new Omidyar Fellows.

Having spent four years at SFI as an Omidyar Fellow before coming to the University of Colorado, Boulder, I feel comfortable asserting that this fellowship is one of the best in higher education: it provides several years of full funding to work on your own big ideas about complex systems and to collaborate with other SFI researchers.

I also feel comfortable saying that SFI tends to prefer young scholars who are already fairly independent, as being an Omidyar Fellow is a lot like being a junior faculty member, except without the teaching responsibilities. No one tells you what to work on. If you have your own interests and your own ideas, this is ideal. SFI also tends to prefer young scholars with a strong quantitative background. If you plan to apply, I recommend writing a fresh research statement (rather than recycling the one you send to university positions) that focuses on your ideas about complex systems and your independent research plans for the next few years.

To help explain just how great a position it is, SFI recently put together a series of short videos, which you can find here.

Deadline: November 1

Apply online for the Omidyar Fellowship.

posted September 6, 2012 07:53 AM in Complex Systems | permalink | Comments (0)

August 18, 2012

Wanting to hire

Postdoctoral Fellowship in Study of Networks

Along with Cris Moore, I am looking to hire a postdoc in the area of complex networks and statistical inference. There are two such positions available, one located at the Santa Fe Institute (working with Cris) and one at the University of Colorado Boulder (working with me). Both are funded by a grant from DARPA to investigate the use of generative models to perform statistical inference in complex networks. The larger team includes Mark Newman at the University of Michigan, and there will be ample opportunity to travel and collaborate among the three institutions.

The grant has a particular emphasis on community detection methods, including methods for detecting changes in community structure in dynamic graphs; functional groups that are not merely "clumps" of densely connected nodes; predicting missing links and identifying spurious ones; building on incomplete or noisy information about the network, generalizing from known attributes of nodes and edges to unknown ones; and identifying surprising or anomalous structures or events.

If you are interested in applying, or know someone who has a strong quantitative background in physics, statistics or computer science, see the application information.

The application deadline is 13 January 2013 with an anticipated start date of May or August 2013.

posted August 18, 2012 11:43 AM in Networks | permalink | Comments (0)

October 17, 2011

Be a postdoc at the Santa Fe Institute, 2012 edition

It's that time of year again: SFI is hiring new Omidyar Fellows.

Appointments begin Fall 2012 and run for two to three years. Having done my own postdoc work at SFI as an Omidyar Fellow, I can tell you that it's an exceptionally good place to be. It's not the place for everyone, and that's the point. It's best for folks who do their best work in unstructured environments, have a good nose for asking fundamental questions, and are comfortable working in a highly interdisciplinary environment.

The deadline to apply is November 1. Here's the official ad:

The Omidyar Postdoctoral Fellowship offers:
• unparalleled intellectual freedom
• transdisciplinary collaboration with leading researchers worldwide
• up to three years in residence in Santa Fe, New Mexico
• discretionary research and collaboration funds
• individualized mentorship and preparation for your next leadership role
• an intimate, creative work environment with an expansive sky

The Omidyar Fellowship at the Santa Fe Institute is unique among postdoctoral appointments. The Institute has no formal programs or departments. Research is collaborative and spans the physical, natural, and social sciences. Most research is theoretical and/or computational in nature, although it may include an empirical component. SFI typically has 15 Omidyar Fellows and postdoctoral researchers, 15 resident faculty, 95 external faculty, and 250 visitors per year. Descriptions of the research themes and interests of the faculty and current Fellows can be found at http://www.santafe.edu/research.

Requirements include a Ph.D. in any discipline (or expect to receive one by September 2012), computational and quantitative skills, an exemplary academic record, a proven ability to work independently and collaboratively, a demonstrated interest in multidisciplinary research and evidence of the ability to think outside traditional paradigms. Applications are encouraged from candidates from any country and discipline. Women and minorities are especially encouraged to apply.

More information is here.

posted October 17, 2011 09:03 PM in Complex Systems | permalink | Comments (0)

August 31, 2010

Be a postdoc at the Santa Fe Institute

It's that time of year again: SFI is hiring new Omidyar Fellows.

Appointments begin Fall 2011. As a newly former Omidyar Fellow, I can tell you that SFI is an exceptionally good place to spend a few years doing research. It's not for everyone, but if you do your best work in unstructured environments, have a good nose for asking fundamental questions, and are comfortable working in a highly interdisciplinary environment, then it's hard to beat the freedom, breadth and resources that SFI provides.

This year's deadline is November 1. Here's the official ad:

Requirements include a Ph.D. in any discipline (or expect to receive one by September 2011), an exemplary academic record, a proven ability to work independently and collaboratively, a demonstrated interest in multidisciplinary research and evidence of the ability to think outside traditional paradigms. Applications are encouraged from candidates from any country and discipline. Women and minorities are especially encouraged to apply.

More information is here.

posted August 31, 2010 01:56 PM in Complex Systems | permalink | Comments (0)

November 12, 2009

Power laws and all that jazz, redux

Long time readers will be very familiar with my interest in power-law distributions (for instance, here and here). So, I'm happy (and relieved) to report that my review article, with Cosma Shalizi and Mark Newman, on methods for fitting and validating power-law distributions in empirical data has finally appeared in print over at SIAM Review. Given that this project started back in late 2004 for me, it's very pleasing to see the finished product in print. This calls for a celebration, for sure.

A. Clauset, C. R. Shalizi and M. E. J. Newman. "Power-law distributions in empirical data." SIAM Review 51(4), 661-703 (2009). (Download the code.)

Power-law distributions occur in many situations of scientiﬁc interest and have signiﬁcant consequences for our understanding of natural and man-made phenomena. Unfortunately, the detection and characterization of power laws is complicated by the large ﬂuctuations that occur in the tail of the distribution -- the part of the distribution representing large but rare events -- and by the diﬃculty of identifying the range over which power-law behavior holds. Commonly used methods for analyzing power-law data, such as least-squares ﬁtting, can produce substantially inaccurate estimates of parameters for power-law distributions, and even in cases where such methods return accurate answers they are still unsatisfactory because they give no indication of whether the data obey a power law at all. Here we present a principled statistical framework for discerning and quantifying power-law behavior in empirical data. Our approach combines maximum-likelihood ﬁtting methods with goodness-of-ﬁt tests based on the Kolmogorov–Smirnov (KS) statistic and likelihood ratios. We evaluate the eﬀectiveness of the approach with tests on synthetic data and give critical comparisons to previous approaches. We also apply the proposed methods to twenty-four real-world data sets from a range of diﬀerent disciplines, each of which has been conjectured to follow a power-law distribution. In some cases we ﬁnd these conjectures to be consistent with the data, while in others the power law is ruled out.

Here's a brief summary of the 24 data sets we looked at, and our conclusions as to how much statistical support there is in the data for them to follow a power-law distribution:

Good:
frequency of words (Zipf's law)

Moderate:
frequency of bird sightings
size of blackouts
book sales
population of US cities
size of religions
severity of inter-state wars
number of citations
papers authored
protein-interaction degree distribution
severity of terrorist attacks

With an exponential cut-off:
size of forest fires
intensity of solar flares
intensity of earthquakes (Gutenberg-Richter law)
popularity of surnames
number of web hits
number of web links, with cut-off
Internet (AS) degree distribution
number of phone calls
size of email address book
number of species per genus

None:
HTTP session sizes
wealth
metabolite degree distribution

posted November 12, 2009 08:19 AM in Complex Systems | permalink | Comments (3)

November 03, 2009

The trouble with community detection

I'm a little (a month!) late in posting it, but here's a new paper, largely by my summer student Ben Good, about the trouble with community detection algorithms.

The short story is that the popular quality function called "modularity" (invented by Mark Newman and Michelle Girvan) admits serious degeneracies that make it somewhat impractical to use in situations where the network is large or has a non-trivial number of communities (a.k.a. modules). At the end of the paper, we briefly survey some ways to potentially mitigate this problem in practical contexts.

The performance of modularity maximization in practical contexts

Benjamin H. Good, Yves-Alexandre de Montjoye, Aaron Clauset, arxiv:0910.0165 (2009).

Although widely used in practice, the behavior and accuracy of the popular module identification technique called modularity maximization is not well understood. Here, we present a broad and systematic characterization of its performance in practical situations. First, we generalize and clarify the recently identified resolution limit phenomenon. Second, we show that the modularity function Q exhibits extreme degeneracies: that is, the modularity landscape admits an exponential number of distinct high-scoring solutions and does not typically exhibit a clear global maximum. Third, we derive the limiting behavior of the maximum modularity Q_max for infinitely modular networks, showing that it depends strongly on the size of the network and the number of module-like subgraphs it contains. Finally, using three real-world examples of metabolic networks, we show that the degenerate solutions can fundamentally disagree on the composition of even the largest modules. Together, these results significantly extend and clarify our understanding of this popular method. In particular, they explain why so many heuristics perform well in practice at finding high-scoring partitions, why these heuristics can disagree on the composition of the identified modules, and how the estimated value of Q_max should be interpreted. Further, they imply that the output of any modularity maximization procedure should be interpreted cautiously in scientific contexts. We conclude by discussing avenues for mitigating these behaviors, such as combining information from many degenerate solutions or using generative models.

posted November 3, 2009 08:55 AM in Networks | permalink | Comments (0)

September 18, 2009

Be a postdoc at SFI

It's that time of year again: SFI is hiring new postdocs.

Appointments begin Fall 2010. As a current postdoc, I can tell you that SFI is an exceptionally good place to spend a few years doing research. It's not for everyone, but if you do your best work in unstructured environments, have a good nose for asking fundamental questions, and are comfortable working in a highly interdisciplinary environment, then it's hard to beat the freedom and resources SFI provides.

This year's deadline is November 2.

The Santa Fe Institute (SFI) will be selectively seeking applications for Omidyar Fellows for 2011, starting in the Fall of 2010. Fellows are appointed for up to three years during which they pursue research questions of their own design and are encouraged to transcend disciplinary lines. SFI’s unique structure and resources enable Fellows to collaborate with members of the SFI faculty, other Fellows, and researchers from around the world.

As the leader in multidisciplinary research, SFI has no formal programs or departments and we accept applications from any field. Research topics span the full range of natural and social sciences and often make connections with the humanities. Most research at SFI is theoretical and/or computational in nature, although some research includes an empirical component in collaboration with other institutions. Descriptions of the research themes and interests of the faculty and current Fellows can be found at http://www.santafe.edu/research/.

Benefits: The compensation package includes a competitive salary and excellent health and retirement benefits. As full participants in the SFI community, Fellows are encouraged to invite speakers, organize workshops and working groups, and engage in research outside their fields. Funds are available to support this full range of research activities.

Requirements: SFI is known for its catalytic research environment and applicants must demonstrate the potential to contribute to this community. Candidates must have a Ph.D. (or expect to receive one by September 2010), an exemplary academic record, and a proven ability to work independently. We expect a demonstrated interest in multidisciplinary research and evidence of the ability to think outside traditional paradigms.

Applications:Applications are welcome from candidates in any country. Successful foreign applicants must acquire an acceptable visa (usually a J-1) as a condition of employment. Women and minorities are especially encouraged to apply. SFI is an equal opportunity employer.

TO APPLY: View the full position announcement and application instructions at www.santafe.edu/education/fellowships-postdoctoral.php. Application due by November 2, 2009. For further information, email ofellowshipinfo@santafe.edu.

posted September 18, 2009 11:01 AM in Complex Systems | permalink | Comments (3)

November 11, 2008

Fellowship: Glasstone Research Fellowships (Oxford, UK)

Mason tells me that Oxford has a pretty good postdoctoral research fellowship gig called the Glasstone Fellowship. The appointment is for up to 3 years, under what looks like pretty general / nebulous guidelines about doing "science." THe fellowship also comes with some travel and research-related funding. Application deadline for the upcoming year is December 8th.

The terms of the bequest restrict the fellowships to “the fields of Botany, Chemistry (Inorganic, Organic or Physical), Engineering, Mathematics, Metallurgy, and Physics”. These will be broadly interpreted; for example Plant Sciences can generally be equated with Botany, Mathematics would include Computer Science and Statistics, Metallurgy can be equated with Materials. The medical sciences, Zoology and Biochemistry (unless related to Plant Sciences) are outside the scope of the scheme.

posted November 11, 2008 12:04 PM in Complex Systems | permalink | Comments (0)

October 22, 2008

SFI is hiring again

I'm a little late in posting the announcement this year, but here it is.

SFI is hiring postdocs again. Appointments begin Fall 2009. As a current postdoc, I can tell you that SFI is an exceptionally good place to spend a few years doing research. It's not for everyone, but if you do your best work in unstructured environments, have a good nose for asking fundamental questions, and are comfortable working in a highly interdisciplinary environment, then it's hard to beat the freedom and resources SFI provides.

This year's deadline is November 14.

Postdoctoral Fellowship appointments at the Santa Fe Institute begin fall 2009. Appointed for up to three years, fellows pursue research questions of their own design, are encouraged to transcend disciplinary lines, and collaborate with SFI faculty, other Fellows, and researchers from around the world. Fellows are encouraged to invite speakers, organize workshops and working groups, and engage in research outside their fields. Funds are available to support this full range of research activities.

The Santa Fe Institute is an affirmative action, equal opportunity employer. We are building a culturally diverse faculty and staff and strongly encourage applications from women, minorities, individuals with disabilities, and covered veterans. Successful foreign applicants must acquire an acceptable visa, usually J-1.

TO APPLY: View the full position announcement and application instructions at www.santafe.edu/postdoc. Application due by November 14, 2008. For further information, email postdocinfo@santafe.edu.

posted October 22, 2008 11:53 AM in Complex Systems | permalink | Comments (0)

August 30, 2007

WNYC on emergence

Radio station WNYC did a 60 minute segment on "emergence" by Jad Abumrad (of WNYC) and Robert Krulwich (of NPR's Science Desk) which is quite well done. Well worth a listen.

The segment features many of the usual suspects. Steve Strogatz talks about firefly synchronization (for instance, did you know that fireflies in Thailand gather in thousands and lightup in time with each other). Deborah Gordon talks about the wildly complex behavior of large groups of ants as compared to the stupid behavior of single ants. Steven Johnson, author Emergence, features several times. And my colleague Iain Couzin makes an appearance to talk about collective behavior. Toward the end, Christof Koch makes an appearance to talk about his collaboration with Francis Crick to figure out how consciousness works. Quite a cast, and Jad does an excellent job of weaving the clips and segments into a compelling whole.

Throughout the piece, there is the consistent theme that the behavior of some systems seems to be more than just the sum of the parts, at least from the typical reductionist perspective that's served science so well in other areas. Ants and brain cells are examples of things that, by themselves, are pretty dumb, but when put together in large numbers, groups of them can acheive complex behavior that often seems highly intelligent. The fundamental question is, How do they do it? Scientists want to know because many of life's complexities (like your brain) are clearly examples of "emergent complexity" and engineers want to know because systems that are emergently complex seem to have other features that we'd like to build into our machines. Characteristics like robustness to failures, adaptability, etc. (Familiar themes, for sure.)

I suspect that physicists are right when they say that emergence has a lot to do with phase transitions, but I think there's more to it than just that. It's probably partly my own biases and training to believe that emergence has a lot to do with computation (of the distributed sort), and thus that computer science is likely to have a great deal to offer. That's the idea at least, and so far, so good.

posted August 30, 2007 04:24 PM in Complex Systems | permalink | Comments (2)

June 08, 2007

Power laws and all that jazz

With apologies to Tolkien:

Three Power Laws for the Physicists, mathematics in thrall,
Four for the biologists, species and all,
Eighteen behavioral, our will carved in stone,
One for the Dark Lord on his dark throne.

In the Land of Science where Power Laws lie,
One Paper to rule them all, One Paper to find them,
One Paper to bring them all and in their moments bind them,
In the Land of Science, where Power Laws lie.

From an interest that grew directly out of my work chracterizing the frequency of severe terrorist attacks, I'm happy to say that the review article I've been working on with Cosma Shalizi and Mark Newman -- on accurately characterizing power-law distributions in empirical data -- is finally finished. The paper covers all aspects of the process, from fitting the distribution to testing the hypothesis that the data is distributed according to a power law, and to make it easy for folks in the community to use the methods we recommend, we've also made our code available.

So, rejoice, rejoice all ye people of Science! Go forth, fit and validate your power laws!

For those still reading, I have a few thoughts about this paper now that it's been released into the wild. First, I naturally hope that people read the paper and find it interesting and useful. I also hope that we as a community start asking ourselves what exactly we mean when we say that such-and-such a quantity is "power-law distributed," and whether our meaning would be better served at times by using less precise terms such as "heavy-tailed" or simply "heterogeneous." For instance, we might simply mean that visually it looks roughly straight on a log-log plot. To which I might reply (a) power-law distributions are not the only thing that can do this, (b) we haven't said what we mean by roughly straight, and (c) we haven't been clear about why we might prefer a priori such a form over alternatives.

The paper goes into the first two points in some detail, so I'll put those aside. The latter point, though, seems like one that's gone un-addressed in the literature for some time now. In some cases, there are probably legitimate reasons to prefer an explanation that assumes large events (and especially those larger than we've observed so far) are distributed according to a power law -- for example, cases where we have some convincing theoretical explanations that match the microscopic details of the system, are reasonably well motivated, and whose predictions have held up under some additional tests. But I don't think most places where power-law distributions have been "observed" have this degree of support for the power-law hypothesis. (In fact, most simply fit a power-law model and assume that it's correct!) We also rarely ask why a system necessarily needs to exhibit a power-law distribution in the first place. That is, would the system behave fundamentally differently, perhaps from a functional perspective, if it instead exhibited a log-normal distribution in the upper tail?

Update 15 June: Cosma also blogs about the paper, making many excellent points about the methods we describe for dealing with data, as well as making several very constructive points about the general affair of power-law research. Well worth the time to read.

posted June 8, 2007 10:00 AM in Complex Systems | permalink | Comments (3)

May 27, 2007

DS07

This week, I'm in Snowbird, UT for SIAM's conference on Applications of Dynamical Systems (DS07). I'm here for a mini-symposium on complex networks organized by Mason Porter and Peter Mucha. I'll be blogging about these (and maybe other) network sessions as time allows (I realize that I still haven't blogged about NetSci last week - that will be coming soon...).

posted May 27, 2007 11:38 PM in Scientifically Speaking | permalink | Comments (1)

May 21, 2007

NetSci 2007

This week, I'm in New York City for the International Conference on Network Science, being held at the New York Hall of Science Museum in Queens. I may not be able to blog each day about the events, but I'll be posting my thoughts and comments as things progress. Stay tuned. In the meantime, here's the conference talk schedule.

posted May 21, 2007 11:41 AM in Scientifically Speaking | permalink | Comments (0)

IPAM - Random and Dynamic Graphs and Networks (Days 4 & 5)

Two weeks ago, I was in Los Angeles for the Institute for Pure and Applied Mathematics' (IPAM, at UCLA) workshop on Random and Dynamic Graphs and Networks; this is the fourth and fifth entry.

Rather than my usual format of summarizing the things that got me thinking during the last few days, I'm going to go with a more free-form approach.

Thursday began with Jennifer Chayes (MSR) discussing some analytical work on adapting convergence-in-distribution proof techniques to ensembles of graphs. She introduced the cut-norm graph distance metric (useful on dense graphs; says that they have some results for sparse graphs, but that it's more difficult for those). The idea of graph distance seems to pop up in many different areas (including several I've been thinking of) and is closely related to the GRAPH ISOMORPHISM problem (which is not known to be NP-complete, but nor is it known to be in P). For many reasons, it would be really useful to be able to calculate in polynomial time the minimum edge-edit distance between two graphs; this would open up a lot of useful techniques based on transforming one graph into another.

Friday began with a talk by Jeannette Janssen (Dalhousie University) on a geometric preferential attachment model, which is basically a geometric random graph but where nodes have a sphere of attraction (for new edges) that has volume proportional to the node's in-degree. She showed some very nice mathematical results on this model. I wonder if this idea could be generalized to arbitrary manifolds (with a distance metric on them) and attachment kernels. That is, imagine that our complex network has actually imbedded on some complicated manifold and the attachment is based on some function of the distance on that manifold between the two nodes. The trick would be then to infer both the structure of the manifold and the attachment function from real data. Of course, without some constraints on both features, it would be easy to construct an arbitrary pair (manifold and kernel) that would give you exactly the network you observed. Is it sufficient to get meaningful results that both should be relatively smooth (continuous, differentiable, etc.)?

Jeannette's talk was followed by Filippo Menczer's talk on mining traffic data from the Internet2/Abilene network. The data set was based on daily dumps of end-to-end communications (packet headers with client and server IDs anonymized) and looked at a variety of behaviors of this traffic. He used this data to construct interaction graphs betwen clients and servers, clients and applications (e.g., "web"), and a few other things. The analysis seems relatively preliminary in the sense that there are a lot of data issues that are lurking in the background (things like aggregated traffic from proxies, aliasing and masking effects, etc.) that make it difficult to translate conclusions about the traffic into conclusions about real individual users. But, fascinating stuff, and I'm looking forward to seeing what else comes out of that data.

The last full talk I saw was by Raissa D'Souza on competition-induced preferential attachment, and a little bit at the end on dynamic geometric graphs and packet routing on them. I've seen the technical content of the preferential attachment talk before, but it was good to have the reminder that power-law distributions are not necessarily the only game in town for heavy-tailed distributions, and that even though the traditional preferential attachment mechanism may not be a good model of the way real growing networks change, it may be that another mechanism that better models the real world can look like preferential attachment. This ties back to Sidney Redner's comment a couple of days before about the citation network: why does the network look like one grown by preferential attachment, when we know that's not how individual authors choose citations?

posted May 21, 2007 11:38 AM in Scientifically Speaking | permalink | Comments (4)

May 09, 2007

IPAM - Random and Dynamic Graphs and Networks (Day 3)

This week, I'm in Los Angeles for the Institute for Pure and Applied Mathematics' (IPAM, at UCLA) workshop on Random and Dynamic Graphs and Networks; this is the third of five entries based on my thoughts from each day. As usual, these topics are a highly subjective slice of the workshop's subject matter...

The impact of mobility networks on the worldwide spread of epidemics

I had the pleasure of introducing Alessandro Vespignani (Indiana University) for the first talk of the day on epidemics in networks, and his work in modeling the effect that particles (people) moving around on the airport network have on models of the spread of disease. I've seen most of this stuff before from previous versions of Alex's talk, but there were several nice additions. The one that struck the audience the most was a visualization of all of the individual flights over the space of a couple of days in the eastern United States; the animation was made by Aaron Koblin for a different project, but was still quite effective in conveying the richness of the air traffic data that Alex has been using to do epidemic modeling and forecasting.

On the structure of growing networks

Sidney Redner gave the pre-lunch talk about his work on the preferential attachment growing-network model. Using the master equation approach, Sid explored an extremely wide variety of properties of the PA model, such as the different regimes of degree distribution behavior for sub-, exact, and different kinds of super- linear attachment rates, the first-mover advantage in the network, the importance of initial degree in determining final degree, along with several variations on the initial model. The power of the master equation approach was clearly evident, I should really learn more about.

He also discussed his work analyzing 100 years of citation data from the Physical Review journal (about 350,000 papers and 3.5 million citations; in 1890, the average number of references in a paper was 1, while in 1990, the average number had increased to 10), particularly with respect to his trying to understand the evidence for linear preferential attachment as a model of citation patterns. Quite surprisingly, he showed that for the first 100 or so citations, papers in PR have nearly linear attachment rates. One point Sid made several times in his talk is that almost all of the results for PA models are highly sensitive to variations in the precise details of the attachment mechanism, and that it's easy to get something quite different (so, no power laws) without trying very hard.

Finally, a question he ended with is why does linear PA seem to be a pretty good model for how citations acrue to papers, even though real citation patterns are clearly not dictated by the PA model?

Panel discussion

The last talk-slot of the day was replaced by a panel discussion, put together by Walter Willinger and chaired by Mark Newman. Instead of the usual situation where the senior people of a field sit on the panel, this panel was composed of junior people (with the expectation that the senior people in the audience would talk anyway). I was asked to sit on the panel, along with Ben Olding (Harvard), Lea Popovic (Cornell), Leah Shaw (Naval Research Lab), and Lilit Yeghiazarian (UCLA). We each made a brief statement about what we liked about the workshop so far, and what kinds of open questions we would be most interested in seeing the community study.

For my on part, I mentioned many of the questions and themes that I've blogged about the past two days. In addition, I pointed out that function is more than just structure, being typically structure plus dynamics, and that our models currently do little to address the dynamics part of this equation. (For instance, can dynamical generative models of particular kinds of structure tell us more about why networks exhibit those structures specifically, and not some other variety?) Lea and Leah also emphasized dynamics as being a huge open area in terms of both modeling and mechanisms, with Lea pointing out that it's not yet clear what are the right kinds of dynamical processes that we should be studying with networks. (I made a quick list of processes that seem important, but only came up with two main caterogies, branching-contact-epidemic-percolation processes and search-navigation-routing processes. Sid later suggested that consensus-voting style processes, akin to the Ising model, might be another, although there are probably others that we haven't thought up yet.) Ben emphasized the issues of sampling, for instance, sampling subgraphs of our model, e.g., the observable WWW or even just the portion we can crawl in an afternoon, and dealing with sampling effects (i.e., uncertainty) in our models.

The audience had a lot to say on these and other topics, and particularly so on the topics of what statisticians can contribute to the field (and also why there are so few statisticians working in this area; some suggestions that many statisticians are only interested in proving asymptotic results for methods, and those that do deal with data are working on bio-informatics-style applications), and on the cultural difference between the mathematicians who want to prove nice things about toy models (folks like Christian Borgs, Microsoft Research) as a way of understanding the general propeties of networks and of their origin, and the empiricists (like Walter Willinger) who want accurate models of real-world systems that they can use to understand their system better. Mark pointed out that there's a third way in modeling, which relies on using an appropriately defined null model as a probe to explore the structure of your network, i.e., a null model that reproduces some of the structure you see in your data, but is otherwise maximally random, can be used to detect the kind of structure the model doesn't explain (so-called "modeling errors", in contrast to "measurement errors"), and thus be used in the standard framework of error modeling that science has used successfully in the past to understand complex systems.

All-in-all, I think the panel discussion was a big success, and the conversation certainly could have gone on well past the one-hour limit that Mark imposed.

posted May 9, 2007 11:38 PM in Scientifically Speaking | permalink | Comments (0)

May 08, 2007

IPAM - Random and Dynamic Graphs and Networks (Day 2)

This week, I'm in Los Angeles for the Institute for Pure and Applied Mathematics' (IPAM, at UCLA) workshop on Random and Dynamic Graphs and Networks; this is the second of five entries based on my thoughts from each day. As usual, these topics are a highly subjective slice of the workshop's subject matter...

Biomimetic searching strategies

Massimo Vergassola (Institut Pasteur) started the day with an interesting talk that had nothing to do with networks. Massimo discussed the basic problem of locating a source of smelly molecules in the macroscopic world where air currents cause pockets of the smell to be sparsely scattered across a landscape, thus spoiling the chemotaxis (gradient ascent) strategy used by bacteria, and a clever solution for it (called "infotaxis") based on trading off exploration and exploitation via an adaptive entropy minimization strategy.

Diversity of graphs with highly variable connectivity

Following lunch, David Alderson (Naval Postgraduate School) described his work with Lun Li (Caltech) on understanding just how different networks with a given degree distribution can be from each other. The take-home message of Dave's talk is, essentially, that the degree distribution is a pretty weak constraint on other patterns of connectivity, and is not a sufficient statistical characterization of the global structure of the network with respect to many (most?) of the other (say, topological and functional) aspects we might care about. Although he focused primarily on degree assortativity, the same kind of analysis could in principle be done for other network measures (clustering coefficient, distribution, diameter, vertex-vertex distance distribution, etc.), none of which are wholly independent of the degree distribution, or of each other! (I've rarely seen the interdependence of these measures discussed (mentioned?) in the literature, even though they are often treated as such.)

In addition to describing his numerical experiments, Dave sounded a few cautionary notes about the assumptions that are often made in the complex networks literature (particularly by theoreticians using random-graph models) on the significance of the degree distribution. For instance, the configration model with a power-law degree sequence (and similarly, graphs constructed via preferential attachment) yields networks that look almost nothing like any real-world graph that we know, except for making vaguely similar degree distributions, and yet they are often invoked as reasonable models of real-world systems. In my mind, it's not enough to simply fix-up our existing random-graph models to instead define an ensemble with a specific degree distribution, and a specific clustering coefficient, and a diameter, or whatever our favorite measures are. In some sense all of these statistical measures just give a stylized picture of the network, and will always be misleading with respect to other important structural features of real-world networks. For the purposes of proving mathematical theorems, I think these simplistic toy models are actually very necessary -- since their strong assumptions make analytic work significantly easier -- so long as we also willfully acknowledge that they are a horrible model of the real world. For the purposes of saying something concrete about real networks, we need more articulate models, and, probably, models that are domain specific. That is, I'd like a model of the Internet that respects the idiosyncracies of this distributed engineered and evolving system; a model of metabolic networks that respects the strangeness of biochemistry; and a model of social networks that understands the structure of individual human interactions. More accurately, we probably need models that understand the function that these networks fulfill, and respect the dynamics of the network in time.

Greedy search in social networks

David Liben-Nowell (Carleton College) then closed the day with a great talk on local search in social networks. The content of this talk largely mirrored that of Ravi Kumar's talk at GA Tech back in January, which covered an empirical study of the distribution of the (geographic) distance covered by friendship links in the LiveJournal network (from 2003, when it had about 500,000 users located in the lower 48 states). This work combined some nice data analysis with attempts to validate some of the theoretical ideas due to Kleinberg for locally navigable networks, and a nice generalization of those ideas to networks with non-uniform population distributions.

An interesting point that David made early in his talk was that homophily is not sufficient to explain the presense of either the short paths that Milgrams' original 6-degrees-of-seperation study demonstrated, or even the existence of a connected social graph! That is, without a smoothly varying notion of "likeness", then homophily would lead us to expect disconnected components in the social network. If both likeness and the population density in the likeness space varied smoothly, then a homophilic social web would cover the space, but the average path length would be long, O(n). In order to get the "small world" that we actually observe, we need some amount of non-homophilic connections, or perhaps multiple kinds of "likeness", or maybe some diversity in the preference functions that individuals use to link to each other. Also, it's still not clear what mechanism would lead to the kind of link-length distribution predicted by Kleinberg's model of optimally navigable networks - an answer to this question would, presumably, tell us something about why modern societies organize themselves the way they do.

posted May 8, 2007 10:52 PM in Scientifically Speaking | permalink | Comments (0)

May 07, 2007

IPAM - Random and Dynamic Graphs and Networks (Day 1)

This week, I'm in Los Angeles for the Institute for Pure and Applied Mathematics' (IPAM, at UCLA) workshop on random and dynamic graphs and networks. This workshop is the third of four in their Random Shapes long program. The workshop has the usual format, with research talks throughout the day, punctuated by short breaks for interacting with your neighbors and colleagues. I'll be trying to do the same for this event as I did for the DIMACS workshop I attended back in January, which is to blog each day about interesting ideas and topics. As usual, this is a highly subjective slice of the workshop's subject matter.

Detecting and understanding the large-scale structure of networks

Mark Newman (U. Michigan) kicked off the morning by discussing his work on clustering algorithms for networks. As he pointed out, in the olden days of network analysis (c. 30 years ago), you could write down all the nodes and edges in a graph and understand its structure visually. These days, our graphs are too big for this, and we're stuck using statistical probes to understand how these things are shaped. And yet, many papers include figures of networks as incoherent balls of nodes and edges (Mark mentioned that Marc Vidal calls these figures "ridiculograms").

I've seen the technical content of Mark's talk before, but he always does an excellent job of making it seem fresh. In this talk, there was a brief exchange with the audience regarding the NP-completeness of the MAXIMUM MODULARITY problem, which made me wonder what exactly are the kind of structures that would make an instance of the MM problem so hard. Clearly, polynomial time algorithms that approximate the maximum modularity Q exist because we have many heuristics that work well on (most) real-world graphs. But, if I was an adversary and wanted to design a network with particularly difficult structure to partition, what kind would I want to include? (Other than reducing another NPC problem using gadgets!)

Walter Willinger raised a point here (and again in a few later talks) about the sensitivity of most network analysis methods to topological uncertainty. That is, just about all the techniques we have available to us assume that the edges as given are completely correct (no missing or spurious edges). Given the classic result due to Watts and Strogatz (1998) of the impact that a few random links added to a lattice have on the diameter of the graph, it's clear that in some cases, topological errors can have a huge impact on our conclusions about the network. So, developing good ways to handle uncertainty and errors while analyzing the structure of a network is a rather large, gaping hole in the field. Presumably, progress in this area will require having good error models of our uncertainty, which, necessary, depend on the measurement techniques used to produce the data. In the case of traceroutes on the Internet, this kind of inverse problem seems quite tricky, but perhaps not impossible.

Probability and Spatial Networks

David Aldous (Berkeley) gave the second talk and discussed some of his work on spatial random graphs, and, in particular, on the optimal design and flow through random graphs. As an example, David gave us a simple puzzle to consider:

Given a square of area N with N nodes distributed uniformly at random throughout. Now, subdivided this area into L^2 subsquares, and choose one node in each square to be a "hub." Then, connect each of the remaining nodes in a square to the hub, and connect the hubs together in a complete graph. The question is, what is the size L that minimizes the total (Euclidean) length of the edges in this network?

He then talked a little about other efficient ways to connect up uniformly scattered points in an area. In particular, Steiner trees are the standard way to do this, and have a cost O(N). The downside for this efficiency is that the tree-distance between physically proximate points on the plane is something polynomial in N (David suggested that he didn't have a rigorous proof for this, but it seems quite reasonable). As it turns out, you can dramatically lower this cost by adding just a few random lines across the plane -- the effect is analagous to the one in the Watts-Strogatz model. Naturally, I was thinking about the structure of real road networks here, and it would seem that the effect of highways in the real world is much the same as David's random lines. That is, it only takes a few of these things to dramatically reduce the topological distance between arbitrary points. Of course, road networks have other things to worry about, such as congestion, that David's highways don't!

posted May 7, 2007 11:49 PM in Scientifically Speaking | permalink | Comments (1)

February 12, 2007

BK21 - Workshop on Complex Systems

Recently, I've been in Korea attending the BK21 Workshop on Complex Systems [1]. The workshop itself was held on Saturday at the Korean Advanced Institute for Science and Technology (KAIST) [2] where Hawoong Jeong played the part of an extremely hospitable host. The workshop's billing was on complex systems in general, but mainly the six invited speakers emphasized complex networks [3]. Here are some thoughts that popped out during, or as a result of, some of the lectures, along with some less specific thoughts.

Methods of Statistical Mechanics in Complex Network Theory
I've enjoyed hearing Juyong Park (Notre Dame University) describe his work on the Exponential Random Graph (ERG) model of networks before, and enjoyed it again today. The ERG model was originally produced by some sociologists and statisticians, but you wouldn't believe it since it fits so well into the statistical mechanics framework. What makes it useful is that, assuming you properly encode your constraints or dynamics into the system, standard statistical mechanics tools let you understand the average features of the resulting set of random graphs. That is, it's a very nice way to define a set of graphs that have particular kinds of structure, but are otherwise random [4].

Even after chatting afterward with Juyong about ERGs in the context of some questions I have on community structure, I'm still not entirely clear how to use this framework to answer complicated questions. It seems that the encoding step I mention above is highly non-trivial, and that even modestly complicated questions, at best, quickly lead first to intractable equations and then to MCMC simulations. At worst, they lead to a wasted day and a broken pencil. Still, if we can develop more powerful tools for the analysis of (realistic) ERG models, I think there's a lot ERGs can offer the field of network theory. I have a personal little goal now to learn enough about ERGs to demonstrate their utility to my students by making them work through some rudimentary calculations with them.

Functional vs Anatomical Connectivity in Complex Brain Networks

Unfortunately, I was somewhat lost during the talk by Changsong Zhou (University of Potsdam) on the dynamics of neuronal networks. Fortunately, while bopping around Seoul's Insadong area a few days later, I had a chance to have him elucidate networks and neuroscience.

Having seen a number of talks on synchronization in complex networks, I've always been puzzled as to why that is the property people seem to care about for dynamic processes on static networks, and not on their information processing or functional behavior. Changsong clarified - if your basic network unit is an oscillator, then synchronization is how information spreads from one location to another. It still seems to me that, at least in neuronal networks, small groups of neurons should behavior more like functional / information processing units rather than like oscillators, but perhaps I'm still missing something here.

The Hierarchical Organization of Network
Oh, and I gave a talk about my work with Mark Newman and Cris Moore on hierarchical random graphs. This was the third (fourth?) time I've given a version of this talk, and I felt pretty good about the set of results I chose to present, and the balance of emphasis I placed on the methodological details and the big picture.

Also, at the last minute before the talk, and because this venue seemed like a good place to make a little plug for statistical rigor, I threw in some slides about the trouble with fitting power laws wily-nily to the tails of distributions [5]. Pleasantly, I saw a lot of nodding heads in the audience during this segment - as if their owners were unconsciously assenting to their understanding. I'd like to think that by showing how power laws and non-power laws can be statistically (and visually!) indistinguishable, most people will be more careful in the language they use in their conclusions and in their modeling assumptions, but I doubt that some will easily give up the comfort that comes with being able to call everything in complex systems a "power law" [6].

Some less specific thoughts
I think a lot of work in the future (or rather, a lot more than has been done in the past) is going to be on biochemical networks. Since biological systems are extremely complicated, this brings up a problem with the way we reduce them to networks, i.e., what we call nodes and what we call edges. For biologists, almost any abstraction we choose is going to be too simple, since it will throw away important aspects like strange neuronal behavior, non-linear dependence, quantum effects, and spatial issues like protein docking. But at the same time, a model that incorporates all of these things will be too complicated to do solve or simulate. My sympathies here actually lay more with the biologists than the networks people (who are mostly physicists), since I'm more interested in understanding how nature actually works than in telling merely plausible stories about the data (which is, in my opinion, what a lot of physicists who work in complex systems do, including those working on networks).

Still, with systems as messy as biological ones, there's a benefit to being able to give an answer at all, even if it's only approximately correct. The hard part in this approach is to accurately estimate the size of the error bars that go with the estimate. That is, rough answers are sufficient (for now) so long as within that roughness lies the true answer. When we use networks built from uncertain data (most networks), and when we use an algorithm-dependent methodology [7] to analyze that data (most analyses), it's not particularly clear how to accurately estimate the corresponding uncertainty in our conclusions. This is a major problem for empirical network science, and I haven't seen many studies handle it well. The moral here is that so long as we don't properly understand how our methods can mislead us, it's not clear what they're actually telling us!

-----

[1] Although I've known about this event for about a month now, I didn't learn until I arrived what the BK21 part meant. BK21 is an educational development program sponsored by the Korean Ministry of Education (jointly with Cornell and Seoul National University) that emphasizes advanced education in seven areas (information technology, biotech, mechanical engineering, chemical engineering, materials science, physics, and chemistry).

[2] KAIST is located in Daejeon, who's main claim to fame is its focus on science and technology - in 1993, Daejeon hosted a three month long international event called Expo '93. On the way into town yesterday, I saw various remnants of the event, including a hill with hedges grown to spell "EXPO '93".

[3] Given the billing, I suppose it's fitting that someone from SFI was there, although its easy to argue these days that "complex systems" is mainstream science, and that complex networks are one of the more visible aspects of the field. What's surprising is that no one from Cornell (the BK21's US partner) was there.

[4] This is very similar to a maximum entropy argument, which physicists adore and machine-learning people are conflicted about.

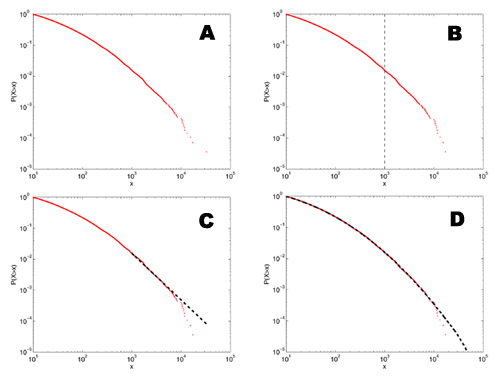
[5]
A: This shows a distribution that we might find in the literature - it has a heavy looking tail that could be a power law, and a slow roll-off in the lower tail.

B: If I eyeball the distribution, at about x=1000, it starts looking particularly straight.

C: If I fit a power-law model to the data above this point, it visually appears to follow the data pretty well. In fact, this kind of fit is much better than many of the ones seen in the physics or biology literature since it's to the cumulative distribution function, rather than the raw density function.

D: The rub, of course, is that this distribution doesn't have a power-law tail at all, but is a log-normal distribution. The only reason it looks like it has a power-law tail is that, for a finite-sized sample, the tail always looks like a power law. The more data we have, the farther out in the tail we have to go to find the "power law" and the steeper the estimated slope will be. If we have some theoretical reason to expect the slope to be less than some value, then this fact may save us from mistaking a lognormal for a power law. The bad news is that it can take a lot more data than we typically have for this to help us.

[6] Power laws have been ridiculously accused of being "the signature of complex systems." Although maybe the person who uttered this statement was being pejorative, in which case, and with much chagrin, I'd have to agree.

[7] What do I mean by "algorithm-dependent methodology"? I basically mean a heuristic approach, i.e., a technique that seems reasonable on the surface, but which ignores whether the solution it produces is correct or optimal. Heuristics often produce "pretty good" solutions, and are often necessary when the optimization version of a problem is hard (e.g., NP-hard). The cost of using a heuristic to find a pretty good solution (in contrast to an approximately correct solution, a la approximation algorithms) is typically that it can also produce quite poor solutions on some problems, and, more importantly here, that they are inherently biased in the range of solutions they do produce. This bias is typically directly a function of the assumptions used to build the heuristic, and, because it can be tricky to analyze, is the reason that uncertainty analysis of heuristics is extremely hard, and thus why computer scientists frown upon their use. Basically, the only reason you should ever use a heuristic is if the more honest methods are too slow for the size of your input. In contrast, an algorithm-independent method is one that is at least unbiased in the way it produces solutions, although it still may not produce an optimum one. MCMC and simulated annealing are examples of unbiased heuristics.

posted February 12, 2007 08:14 AM in Complex Systems | permalink | Comments (0)

February 03, 2007

Modernizing Kevin Bacon

Via Mason Porter and Arcane Gazebo comes a pointer to a modernization (geekification?) of the Kevin Bacon game, this time using Wikipedia (and suitably enough, this version has its own wikipedia page). Here's how it works:

Go to Wikipedia.
Click the random article link in the sidebar.
Open a second random article in another tab.
Try to find a chain of links (as short as possible) starting from the first article that leads to the second.

Many people are fascinated by the fact that these short paths, which is popularly called the "small world phenomenon." This behavior isn't really so amazing, since even purely random graphs have very short paths between arbitrary nodes. What makes the success of these games truly strange is the fact that we can find these short paths using only the information at our current location in the search, and some kind of mental representation of movies and actors / human knowledge and concepts. That is, both the movie-actors network and wikipedia are locally navigable.

The US road system is only partially navigable in this sense. For instance, with only a rudimentary mental map of the country, you could probably get between major cities pretty easily using only the information you see on highway signs. But, cities are not locally navigable because the street signs give you no indication of where to find anything. In order to efficiently navigate them, you either need a global map of the city in hand, or a complex mental map of the city (this is basically what cab drivers do it, but they devote a huge amount of mental space to creating it).

Mason also points me to a tool that will find you the shortest path between two wikipedia articles. However, I'm sure this program isn't finding the path the way a human would. Instead, I'm sure that it's just running a breadth-first search from both pages and returning the path formed when the two trees first touch. What would be more interesting, I think, would be a lexicographic webcrawler that would navigate from the one page to the other using only the text available on its current page (and potentially its history of where it's been), and some kind of simple model of concepts / human knowledge (actually, it would only need a function to tell it whether one concept is closer to its target or not). If such a program could produce chains between random articles that are about as short as those that humans produce, then that would be pretty impressive.

(These questions all relate to the process of navigation on a static network, but an equally important question is the one about how the network produces the structure necessary to be locally navigable in the first place. Although it's a highly idealized and unrealistic model, I humbly point to the results of my first big research project in graduate school as potentially having something to say on this topic.)

posted February 3, 2007 03:09 PM in Complex Systems | permalink | Comments (0)

November 25, 2006

Unreasonable effectiveness (part 3)

A little more than twenty years after Hamming's essay, the computer scientist Bernard Chazelle penned an essay on the importance of the algorithm, in which he offers his own perspective on the unreasonable effectiveness of mathematics.

Mathematics shines in domains replete with symmetry, regularity, periodicity -- things often missing in the life and social sciences. Contrast a crystal structure (grist for algebra's mill) with the World Wide Web (cannon fodder for algorithms). No math formula will ever model whole biological organisms, economies, ecologies, or large, live networks.

Perhaps this, in fact, is what Hamming meant by saying that much of physics is logically deducible, that the symmetries, regularities, and periodicities of physical nature constrain it in such strong ways that mathematics alone (and not something more powerful) can accurately capture its structure. But, complex systems like organisms, economies and engineered systems don't have to, and certainly don't seem to, respect those constraints. Yet, even these things exhibit patterns and regularities that we can study.

Clearly, my perspective matches Chazelle's, that algorithms offer a better path toward understanding complexity than the mathematics of physics. Or, to put it another way, that complexity is inherently algorithmic. As an example of this kind of inherent complexity through algorithms, Chazelle cites Craig Reynolds' boids model. Boids is one of the canonical simulations of "artificial life"; in this particular simulation, a trio of simple algorithmic rules produce surprisingly realistic flocking / herding behavior when followed by a group of "autonomous" agents [1]. There are several other surprisingly effective algorithmic models of complex behavior (as I mentioned before, cellular automata are perhaps the most successful), but they all exist in isolation, as models of disconnected phenomenon.

So, I think one of the grand challenges for a science of complexity will be to develop a way to collect the results of these isolated models into a coherent framework. Just as we have powerful tools for working with a wide range of differential-equation models, we need similar tools for working with competitive agent-based models, evolutionary models, etc. That is, we would like to be able to write down the model in an abstract form, and then draw strong, testable conclusions about it, without simulating it. For example, imagine being able to write down Reynolds' three boids rules and deriving the observed flocking behavior before coding them up [2]. To me, that would prove that the algorithm is unreasonably effective at capturing complexity. Until then, it's just a dream.

Note: See also part 1 and part 2 of this series of posts.

[1] This citation is particularly amusing to me considering that most computer scientists seem to be completely unaware of the fields of complex systems and artificial life. This is, perhaps, attributable to computer science's roots in engineering and logic, rather than in studying the natural world.

[2] It's true that problems of intractability (P vs NP) and undecidability lurk behind these questions, but analogous questions lurk behind much of mathematics (Thank you, Godel). For most practical situations, mathematics has sidestepped these questions. For most practical situations (where here I'm thinking more of modeling the natural world), can we also sidestep them for algorithms?

posted November 25, 2006 01:19 PM in Things to Read | permalink | Comments (0)

November 24, 2006

Unreasonable effectiveness (part 2)

In keeping with the theme [1], twenty years after Wigner's essay on The Unreasonable Effectiveness of Mathematics in the Natural Sciences, Richard Hamming (who has graced this blog previously) wrote a piece by the same name for The American Mathematical Monthly (87 (2), 1980). Hamming takes issue with Wigner's essay, suggesting that the physicist has dodged the central question of why mathematics has been so effective. In Hamming's piece, he offers a few new thoughts on the matter: primarily, he suggests, mathematics has been successful in physics because much of it is logically deducible, and that we often change mathematics (i.e., we change our assumptions or our framework) to fit the reality we wish to describe. His conclusion, however, puts the matter best.

From all of this I am forced to conclude both that mathematics is unreasonably effective and that all of the explanations I have given when added together simply are not enough to explain what I set out to account for. I think that we -- meaning you, mainly -- must continue to try to explain why the logical side of science -- meaning mathematics, mainly -- is the proper tool for exploring the universe as we perceive it at present. I suspect that my explanations are hardly as good as those of the early Greeks, who said for the material side of the question that the nature of the universe is earth, fire, water, and air. The logical side of the nature of the universe requires further exploration.

Hamming, it seems, has dodged the question as well. But, Hamming's point that we have changed mathematics to suit our needs is important. Let's return to the idea that computer science and the algorithm offer a path toward capturing the regularity of complex systems, e.g., social and biological ones. Historically, we've demanded that algorithms yield guarantees on their results, and that they don't take too long to return them. For example, we want to know that our sorting algorithm will actually sort a list of numbers, and that it will do it in the time I allow. Essentially, our formalisms and methods of analysis in computer science have been driven by engineering needs, and our entire field reflects that bias.

But, if we want to use algorithms to accurately model complex systems, it stands to reason that we should orient ourselves toward constraints that are more suitable for the kinds of behaviors those systems exhibit. In mathematics, it's relatively easy to write down an intractable system of equations; similarly, it's easy to write down an algorithm who's behavior is impossible to predict. The trick, it seems, will be to develop simple algorithmic formalisms for modeling complex systems that we can analyze and understand in much the same way that we do for mathematical equations.

I don't believe that one set of formalisms will be suitable for all complex systems, but perhaps biological systems are consistent enough that we could use one set for them, and perhaps another for social systems. For instance, biological systems are all driven by metabolic needs, and by a need to maintain structure in the face of degradation. Similarly, social systems are driven by, at least, competitive forces and asymmetries in knowledge. These are needs that things like sorting algorithms have no concept of.

Note: See also part 1 and part 3 of this series of posts.

[1] A common theme, it seems. What topic wouldn't be complete without its own wikipedia article?

posted November 24, 2006 12:21 PM in Things to Read | permalink | Comments (2)

November 23, 2006

Unreasonable effectiveness (part 1)

Einstein apparently once remarked that "The most incomprehensible thing about the universe is that it is comprehensible." In a famous paper in Pure Mathematics (13 (1), 1960), the physicist Eugene Wigner (Nobel in 1963 for atomic theory) discussed "The Unreasonable Effectiveness of Mathematics in the Natural Sciences". The essay is not too long (for an academic piece), but I think this example of the the application of mathematics gives the best taste of what Wigner is trying to point out.

The second example is that of ordinary, elementary quantum mechanics. This originated when Max Born noticed that some rules of computation, given by Heisenberg, were formally identical with the rules of computation with matrices, established a long time before by mathematicians. Born, Jordan, and Heisenberg then proposed to replace by matrices the position and momentum variables of the equations of classical mechanics. They applied the rules of matrix mechanics to a few highly idealized problems and the results were quite satisfactory.

However, there was, at that time, no rational evidence that their matrix mechanics would prove correct under more realistic conditions. Indeed, they say "if the mechanics as here proposed should already be correct in its essential traits." As a matter of fact, the first application of their mechanics to a realistic problem, that of the hydrogen atom, was given several months later, by Pauli. This application gave results in agreement with experience. This was satisfactory but still understandable because Heisenberg's rules of calculation were abstracted from problems which included the old theory of the hydrogen atom.

The miracle occurred only when matrix mechanics, or a mathematically equivalent theory, was applied to problems for which Heisenberg's calculating rules were meaningless. Heisenberg's rules presupposed that the classical equations of motion had solutions with certain periodicity properties; and the equations of motion of the two electrons of the helium atom, or of the even greater number of electrons of heavier atoms, simply do not have these properties, so that Heisenberg's rules cannot be applied to these cases.

Nevertheless, the calculation of the lowest energy level of helium, as carried out a few months ago by Kinoshita at Cornell and by Bazley at the Bureau of Standards, agrees with the experimental data within the accuracy of the observations, which is one part in ten million. Surely in this case we "got something out" of the equations that we did not put in.

As someone (apparently) involved in the construction of "a physics of complex systems", I have to wonder whether mathematics is still unreasonably effective at capturing these kind of inherent patterns in nature. Formally, the kind of mathematics that physics has historically used is equivalent to a memoryless computational machine (if there is some kind of memory, it has to be explicitly encoded into the current state); but, the algorithm is a more general form of computation that can express ideas that are significantly more complex, at least partially because it inherently utilizes history. This suggests to me that a physics of complex systems will be intimately connected to the mechanics of computation itself, and that select tools from computer science may ultimately let us express the structure and behavior of complex, e.g., social and biological, systems more effectively than the mathematics used by physics.

One difficulty in this endeavor, of course, is that the mathematics of physics is already well-developed, while the algorithms of complex systems are not. There have been some wonderful successes with algorithms already, e.g., cellular automata, but it seems to me that there's a significant amount of cultural inertia here, perhaps at least partially because there are so many more physicists than computer scientists working on complex systems.

Note: See also part 2 and part 3 of this series of posts.

posted November 23, 2006 11:31 AM in Things to Read | permalink | Comments (2)