November 17, 2009
How big is a whale?
One thing I've been working on recently is a project about whale evolution [1]. Yes, whales, those massive and inscrutable aquatic mammals that are apparently the key to saving the world [2]. They've also been called the poster child of macroevolution, which is why I'm interested in them, due to their being so incredibly different from their closest living cousins, who still have four legs and nostrils on the front of their face.








Part of this project requires understanding something about how whale size (mass) and shape (length) are related. This is because in some cases, it's possible to get a notion of how long a whale is (for example, a long dead one buried in Miocene sediments), but it's generally very hard to estimate how heavy it is. [3]
This goes back to an old question in animal morphology, which is whether size and shape are related geometrically or elastically. That is, if I were to double the mass of an animal, would it change its body shape in all directions at once (geometric) or mainly in one direction (elastic)? For some species, like snakes and cloven-hoofed animals (like cows), change is mostly elastic; they mainly get longer (snakes) or wider (bovids, and, some would argue, humans) as they get bigger.
About a decade ago, Marina Silva [4], building on earlier work [5], tackled this question quantitatively for about 30% of all mammal species and, unsurprisingly I think, showed that mammals tend grow geometrically as they change size. In short, yes, mammals are generally spheroids, and L = (const.) x M^(1/3). This model is supposed to be even better for whales: because they're basically neutrally buoyant in water, gravity plays very little role in constraining their shape, and thus there's less reason for them to deviate from the geometric model [6].
Collecting data from primary sources on the length and mass of living whale species, I decided to reproduce Silva's analysis [7]. In this case, I'm using about 2.5 times as much data as Silva had (n=31 species versus n=77 species), so presumably my results are more accurate. Here's a plot of log mass versus log length, which shows a pretty nice allometric scaling relationship between mass (in grams) and length (in meters):
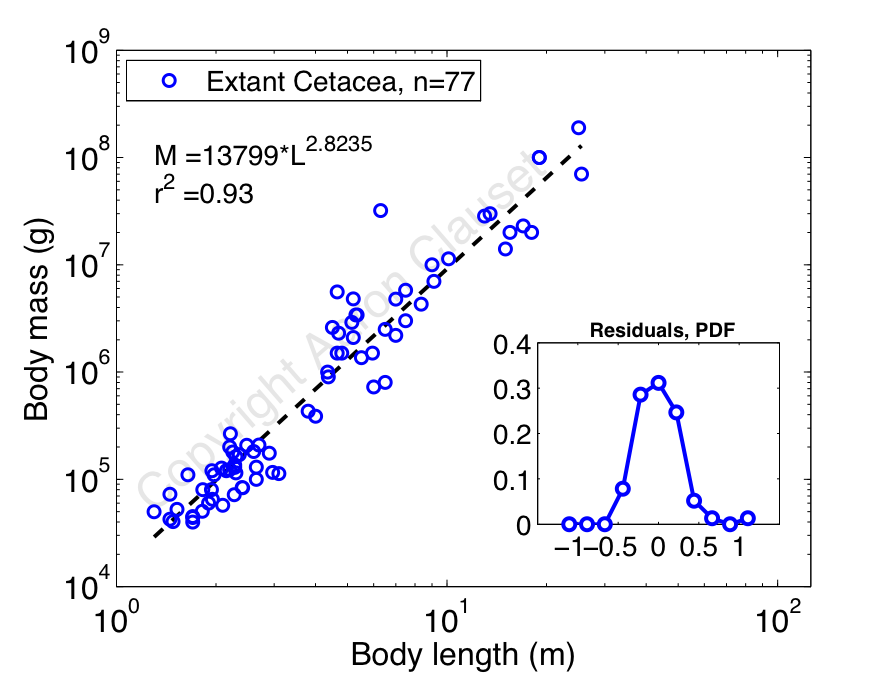
Aside from the fact that mass and length relate very closely, the most interesting thing here is that the estimated scaling exponent is less than 3. If we take the geometric model at face value, then we'd expect the mass of a whole whale to simply be its volume times its density, or
where k_1 and k_2 scale the lengths of the two minor axes (its widths, front-to-back and left-to-right) relative to the major axis (its length L, nose-to-tail), and the trailing constant is the density of whale flesh (here, assumed to be the density of water) [8].
If the constants k_1 and k_2 are the same for all whales (the simplest geometric model), then we'd expect a cubic relation: M = (const.) x L^3. But, our measured exponent is less than 3. So, this implies that k_1 and k_2 cannot be constants, and must instead increase slightly with greater length L. Thus, as a whale gets longer, it gets wider less quickly than we expect from simple geometric scaling. But, that being said, we can't completely rule out the hypothesis that the scatter around the regression line is obscuring a beautifully simple cubic relation, since the 95% confidence intervals around the scaling exponent do actually include 3, but just barely: (2.64, 3.01).
So, the evidence is definitely in the direction of a geometric relationship between a whale's mass and length. That is, to a large extent, a blue whale, which can be 80 feet long (25m), is just a really(!) big bottlenose dolphin, which are usually only 9 feet long (2.9m). That being said, the support for the most simplistic model, i.e., strict geometric scaling with constant k_1 and k_2, is marginal. Instead, something slightly more complicated happens, with a whale's circumference growing more slowly than we'd expect. This kind of behavior could be caused by a mild pressure toward more hydrodynamic forms over the simple geometric forms, since the drag on a longer body should be slightly lower than the drag on a wider body.
Figuring out if that's really the case, though, is beyond me (since I don't know anything about hydrodynamics and drag) and the scope of the project. Instead, it's enough to be able to make a relatively accurate estimation of body mass M from an estimate of body length L. Plus, it's fun to know that big whales are mostly just scaled up versions of little ones.
More about why exactly I need estimates of body mass for will have to wait for another day.
Update 17 Nov. 2009: Changed the 95% CI to 3 significant digits; tip to Cosma.
Update 29 Nov. 2009: Carl Zimmer, one of my favorite science writers, has a nice little post about the way fin whales eat. (Fin whales are almost as large as blue whales, so presumably the mechanics are much the same for blue whales.) It's a fascinating piece, involving the physics of parachutes.
-----
[0] The pictures are, left-to-right, top-to-bottom: blue whale, bottlenose dolphin, humpback whale, sperm whale, beluga, narwhal, Amazon river dolphin, and killer whale.
[1] Actually, I mean Cetaceans, but to keep things simple, I'll refer to whales, dolphins, and porpoises as "whales".
[2] Thankfully, the project doesn't involve networks of whales... If that sounds exciting, try this: D. Lusseau et al. "The bottlenose dolphin community of Doubtful Sound features a large proportion of long-lasting associations. Can geographic isolation explain this unique trait?" Behavioral Ecology and Sociobiology 54(4): 396-405 (2003).
[3] For a terrestrial mammal, it's possible to estimate body size from the shape of its teeth. Basically, mammalian teeth (unlike reptilian teeth) are highly differentiated and certain aspects of their shape correlate strongly with body mass. So, if you happen to find the first molar of a long dead terrestrial mammal, there's a biologist somewhere out there who can tell you both how much it weighed and what it probably ate, even if the tooth is the only thing you have. Much of what we know about mammals from the Jurassic and Triassic, when dinosaurs were dominant, is derived from fossilized teeth rather than full skeletons.
[4] Silva, "Allometric scaling of body length: Elastic or geometric similarity in mammalian design." J. Mammology 79, 20-32 (1998).
[5] Economos, "Elastic and/or geometric similarity in mammalian design?" J. Theoretical Biology 103, 167-172 (1983).
[6] Of course, fully aquatic species may face other biomechanical constraints, due to the drag that water exerts on whales as they move.
[7] Actually, I did the analysis first and then stumbled across her paper, discovering that I'd been scooped more than a decade ago. Still, it's nice to know that this has been looked at before, and that similar conclusions were arrived at.
[8] Blubber has a slight positive buoyancy, and bone has a negative buoyancy, so this value should be pretty close to the true average density of a whale.
posted November 17, 2009 04:33 PM in Evolution | permalink | Comments (2)
January 07, 2009
Synthesizing biofuels
Carl Zimmer is one of my favorite science writers. And while I was in the Peruvian Amazon over the holidays, I enjoyed reading his book on parasites Parasite Rex. This way, if I managed to pick up malaria while I was there, at least I'd now know what a beautifully well adapted parasite I would have swimming in my veins.
But this post isn't about parasites, or even about Carl Zimmer. It's about hijacking bacteria to do things we humans care about. Zimmer's most recent book Microcosm is about E. coli and the things that scientists have learned about how cells work (and thus all of biology). And one of the things we've learned is how to manipulate E. coli to manufacture proteins or other molecules desired by humans. For science, this kind of reprogramming is incredibly useful and allows a skilled scientist to probe the inner workings of the cell even more deeply. This potential helped the idea gain the label "breakthrough of the year" in the last issue in 2008 of Science magazine.
This idea of engineering bacteria to do useful things for humanity, of course, is not a new one. I first encountered it almost 20 years ago in John Brunner's 1968 novel Stand on Zanzibar in a scene where a secret agent, standing over the inflatable rubber raft he just used to surreptitiously enter a foreign country, empties a vial of bacterium onto the raft that is specially engineering to eat the rubber. As visions of the future go, this kind of vision, in which humans use biology to perform magic-like feats, is in stark contrast to the future envisioned by Isaac Asimov's short stories on robots. Asimov foresaw a world dominated by, basically, advanced mechanical engineering. His robots were made of metal and other inorganic materials and humanity performed magic-like feats by understanding physics and computation.
Which is the more likely future? Both, I'd say, but in some respects, I think there's greater potential in the biological one and there are already people who are making that future a reality. Enter our favorite biological hacker Craig Venter. Zimmer writes in a piece (here) for Yale Environment 360 about Venter's efforts to new apply his interest in reprogramming bacteria in the direction of mass-producing alternative fuels.
The idea is to take ordinary bacteria and their cellular machinery for producing organic molecules (perhaps even simple hydrocarbons), and reprogram or augment them with new metabolic pathways that convert cheap and abundant organic material (sugar, sewage, whatever) into fuel like gasoline or diesel. That is, we would use most of the highly precise and relatively efficient machinery that evolution has produced to accomplish other tasks, and adapt it slightly for human purposes. The ideal result from this kind of technology would be to take photosynthetic organisms, such as algae, and have them suck CO2 and H2O out of the atmosphere to directly produce fuel. (As opposed to use other photosynthetic organisms like corn or sugarcane to produce an intermediate than can be eventually converted into fuel, as is the case for ethanol.) This would essentially use solar power to drive in reverse the chemical reactions that run the internal combustion engine, and would have effectively zero CO2 emissions. In fact, this direct approach to synthesizing biofuels using microbes is exactly what Venter is now doing.
The devil, of course, is in the details. If these microbe-based methods end up being anything like current methods of producing ethanol for fuel, they could end up being worse for the environment than fossil fuels. And there's also some concern about what might happen if these human-altered microbes escaped into the wild (just as there's concern about genetically modified food stocks jumping into wild populations). That being said, I doubt there's much to be worried about on that point. Wild populations have very different evolutionary pressures than domesticated stocks do, and evolution is likely to weed out human-inserted genes unless they're actually useful in the wild. For instance, cows are the product of a long chain of human-guided evolution and are completely dependent on humans for their survival now. If humans were to disappear, cows would not last long in the wild. Similarly, humans have, for a very long time now, already been using genetically-altered microbes to produce something we like, i.e., yogurt, without much danger to wild populations.
From microbe-based synthesis of useful materials, it's a short jump to microbe-mediated degradation of materials. Here, I recall an intriguing story about a high school student's science project that yielded some promising results for evolving (through human-guided selection) a bacteria that eats certain kinds of plastic. Maybe we're not actually that far from realizing certain parts of Brunner's vision for the future. Who knows what reprogramming will let us do next?
posted January 7, 2009 08:19 AM in Global Warming | permalink | Comments (0)
August 26, 2008
Cows are magnets.
Hot off the press at the Proceedings of the National Academy of Science is an article about magnetoreception in cows and deer [1]. Begall and colleagues, perhaps having spent far too much time playing with Google Earth, noticed that grazing cows and deer [2] seem to slightly prefer aligning themselves N-S, like magnets in the Earth's magnetic field. From the abstract
To test the hypothesis that cattle orient their body axes along the field lines of the Earth's magnetic field, we analyzed the body orientation of cattle from localities with high magnetic declination. Here, magnetic north was a better predictor than geographic north. [3]
Time to rewrite the physics textbooks, I guess: Cows are spheres, yes, but magnetic spheres!
-----
[1] S. Begall, J. Cerveny, J. Neef, O. Vojtech and H. Burda, "Magnetic alignment in grazing and resting cattle and deer." PNAS 105, 13451-13455 (2008).
[2] I was very disappointed, when I read through the article itself, to find no satellite pictures of cows aligned N-S. Indeed, there was not a single picture of a cow (or deer)!
[3] This is a good control to test the possibility that the E-W orientation of the sun drove the animals to prefer N-S in order to maximize the absorbed solar radiation. So, it seems that there really is some kind of weak magnetoreception going on. Now it's a matter of figuring out what biological compounds convey this magnetic sensitivity, and how its response to the Earth's field percolates up to behavioral tendencies.
posted August 26, 2008 10:59 AM in Things that go squish | permalink | Comments (3)
July 21, 2008
Evolution and Distribution of Species Body Size
One of the most conspicuous and most important characteristics of any organism is its size [1]: the size basically determines the type of physics it faces, i.e., what kind of world it has to live in. For instance, bacteria live in a very different world from insects, and insects live in a very different world from most mammals. In a bacterium's world, nanometers and micrometers are typical scales and some quantum effects are significant enough to drive some behaviors, but larger-scale effects like surface tension and gravity have a much more indirect effect. For most insects, typical scales are millimeter and centimeters, where quantum effects are negligible, but the surface tension of water matters tremendously. Similarly, for most mammals [2], a typical scale is more like a meter, and surface tension isn't as important as gravity and supporting your own body weight.
And yet despite these vast differences in the basic physical world that different types of species encounter, the distribution of body sizes within a taxonomic group, that is, the relative number of small, medium and large species, seems basically the same regardless of whether we're talking about insects, fish, birds or mammals: a few species in a given group are very small (about 2 grams for mammals), most species are slightly larger (between 20 and 80 grams for mammals), but some species are much (much!) larger (like elephants, which weigh over 1,000,000 times more than the smallest mammal). The ubiquity of this distribution has intrigued biologists since they first began to assemble large data sets in the second-half of the 20th century.
Many ideas have been suggested about what might cause this particular, highly asymmetric distribution, and they basically group into two kinds of theories: optimal body-size and diffusion. My interest in answering this question began last summer, partly as a result of some conversations with Alison Boyer in another context. Happily, the results of this project were published in Science last week [3] and basically show that the diffusion explanation is, when fossil data is taken in account, really quite good. (I won't go into the optimal body-size theories here; suffice to say that it's not as popular a theory as the diffusion explanation.) At its most basic, the paper shows that, while there are many factors that influence whether a species gets bigger or smaller as it evolves over long periods of time, their combined influence can be modeled as a simple random walk [4]. For mammals, the diffusion process is, surprisingly I think, not completely agnostic about the current size of a species. That is, although a species experiences many different pressures to get bigger or smaller, the combined pressure typically favors getting a little bigger (but not always). The result of this slight bias toward larger sizes is that descendent species are, on average, 4% larger than their ancestors.
But, the diffusion itself is not completely free [5], and its limitations turn out to be what cause the relative frequencies of large and small species to be so asymmetric. On the low end of the scale, there are unique problems that small species face that make it hard to be small. For instance, in 1948, O. P. Pearson published a one-page paper in Science reporting work where he, basically, stuck a bunch of small mammals in an incubator and measured their oxygen (O2) consumption. What he discovered is that O2 consumption (a proxy for metabolic rate) goes through the roof near 2 grams, suggesting that (adult) mammals smaller than this size might not be able to find enough high-energy food to survive, and that, effectively, 2 grams is the lower limit on mammalian size [6]. On the upper end, there is an increasingly dire long-term risk of become extinct the bigger a species is. Empirical evidence, both from modern species experiencing stress (mainly from human-related sources) as well as fossil data, suggests that extinction seems to kill off larger species more quickly than smaller species, with the net result being that it's hard to be big, too.
Together, this hard lower-limit and soft upper-limit on the diffusion of species sizes shape distribution of species in an asymmetric way and create the distribution of species sizes we see today [7]. To test this hypothesis in a strong way, we first estimated the details of the diffusion model (such as the location of the lower limit and the strength of the diffusion process) from fossil data on about 1100 extinct mammals from North America that ranged from 100 million years ago to about 50,000 years ago. We then simulated about 60 million years of mammalian evolution (since dinosaurs died out), and discovered that the model produced almost exactly the size distribution of currently living mammals. Also, when we removed any piece of the model, the agreement with the data became significantly worse, suggesting that we really do need all three pieces: the lower limit, the size-dependent extinction risk, and the diffusion process. The only thing that wasn't necessary was, surprisingly, the bias toward slightly larger species in the diffusion itself [8], which I think most people thought was necessary to produce really big species like elephants.
Although this paper answers several questions about why the distribution of species body size is the way it is, there are several questions left unanswered, which I might try to work on a little in the future. In general, one exciting thing is that this model offers some possibilities for connecting macroevolutionary patterns, such as the distribution of species body sizes over evolutionary time, with ecological processes, such as the ones that make larger species become extinct more quickly than small species, in a relatively compact way. That gives me some comfort, since I'm sympathetic to the idea that there are reasons we see such distinct patterns in the aggregate behavior of biology, and that it's possible to understand something about them without having to understand the specific details of every species and every environment.
-----
[1] An organism's size is closely related, but not exactly the same as its mass. For mammals, their density is very close to that of water, but plants and insects, for instance, can be less or more dense than water, depending on the extent of specialized structures.
[2] The typical mammal species weights about 40 grams, which is the size of the Pacific rat. The smallest known mammal species are the Etruscan shrew and the bumblebee bat, both of whom weight about 2 grams. Surprisingly, there are several insect species that are larger, such as the titan beetle which is known to weigh roughly 35 grams as an adult. Amazingly, there are some other species that are larger still. Some evidence suggests that it is the oxygen concentration in the atmosphere that mainly limits the maximum size of insects. So, about 300 million years ago, when the atmospheric oxygen concentrations were much higher, it should be no surprise that the largest insects were also much larger.
[3] A. Clauset and D. H. Erwin, "The evolution and distribution of species body size." Science 321, 399 - 401 (2008).
[4] Actually, in the case of body size variation, the random walk is multiplicative meaning that changes to species size are more like the way your bank balance changes, in which size increases or decreases by some percentage, and less like the way a drunkard wanders, in which size changes by increasing or decreasing by roughly constant amounts (e.g., the length of the drunkard's stride).
[5] If it were a completely free process, with no limits on the upper or lower ends, then the distribution would be a lot more symmetric than it is, with just as many tiny species as enormous species. For instance, with mammals, an elephant weights about 10 million grams, and there are a couple of species in this range of size. A completely free process would thus also generate a species that weighed about 0.000001 grams. So, the fact that the real distribution is asymmetric implies that some constraints much exist.
[6] The point about adult size is actually an important one, because all mammals (indeed, all species) begin life much smaller. My understanding is that we don't really understand very well the differences between adult and juvenile metabolism, how juveniles get away with having a much higher metabolism than their adult counterparts, or what really changes metabolically as a juvenile becomes an adult. If we did, then I suspect we would have a better theoretical explanation for why adult metabolic rate seems to diverge at the lower end of the size spectrum.
[7] Actually, we see fewer large species today than we might have 10,000 - 50,000 years ago, because an increasing number of them have died out. The most recent population collapses are certainly due to human activities such as hunting, habitat destruction, pollution, etc., but even 10,000 years ago, there's some evidence that the disappearnace of the largest species was due to human activities. To control for this anthropic influence, we actually used data on mammal species from about 50,000 years ago as our proxy for the "natural" state.
[8] This bias is what's more popularly known as Cope's rule, the modern reformulation of Edward Drinker Cope's suggesting that species tend to get bigger over evolutionary time.
posted July 21, 2008 03:01 PM in Evolution | permalink | Comments (0)
February 11, 2008
Food for thought (1)
posted February 11, 2008 08:31 PM in Pleasant Diversions | permalink | Comments (0)
July 05, 2007
Boulder School on Biophysics
Blogging this month will be light as I'm attending the Boulder School on Biophysics (ostensibly the Boulder School is about condensed matter, but the main topic changes each year and this year it's about squishy (soft) condensed matter). The talks so far remind me of how much easier good modeling is when you're constrained to 3 spatial dimensions and basically know what kind of forces you'll need to deal with in order to get relatively realistic behavior (at a variety of levels of realism). In the world of networks, we don't have these kinds of constraints and so coming up with reasonable mechanisms is significantly harder. As with biology, the data analysis for networks has advanced much more quickly than has the theory, precisely, I imagine, for this reason. Later in the school, there will be some presentations on micro-biological networks, which I'm looking forward to. These systems seem like more reasonable objects for good modeling than are things like the Internet, since we can actually do controlled experiments on many of them to see how well the theories hold up.
A few things I've learned so far.
Chromosomes seem to behave a lot like jointed chains wiggling around in solution, and yet they also tend to maintain their position inside the nucleus, suggesting some sort of tethering behavior -- a behavior that has been implicated as a mechanical gene-regulation mechanism. Similar tethering behavior seems to appear in prokaryotic cells as well. There's the suggestion that spatial location of genes has an important role in their expression levels and general regulation (a result known by experimental micro-biologists, but not well understood theoretically).
Histones (those bits of protein that DNA wraps itself around at regular intervals over the entire length of the chromosome) are also implicated in regulation, basically by making it more difficult to transcribe a gene when its start codon is in the middle of one of the turns around the histone; also, histones seem to have a preferred sequence of DNA for binding; the suggestion is that the copious amounts of repeated sequences in the genome may be related to binding these objects in a regular fashion.
Motor proteins are fascinating squishy things. Your muscles are composed of large quantities of myosin motor proteins that crawl along actin filaments by exerting a tiny force of a few tens of pico-newtons (it would take tens of billion of these to exert the equivalent force that the Earth exerts on an apple).
posted July 5, 2007 07:37 PM in Things that go squish | permalink | Comments (0)
June 28, 2007
Hacking microbiology
Two science news articles (here and here) about J. Craig Venter's efforts to hack the genome (or perhaps, more broadly, hacking microbiology) reminded me of a few other articles about his goals. The two articles I ran across today concern a rather cool experiment where scientists took the genome of one bacterium species (M. mycoides) and transplanted it into a closely related one (M. capricolum). The actual procedure by which they made the genome transfer seems rather inelegant, but the end result is that the donor genome replaced the recepient genome and was operating well enough that the recepient looked like the donor. (Science article is here.) As a proof of concept, this experiment is a nice demonstration that the cellular machinery of the the recepient species is similar enough to that of the donor that it can run the other's genomic program. But, whether or not this technique can be applied to other species is an open question. For instance, judging by the difficulties that research on cloning has encountered with simply transferring a nucleus of a cell into an unfertilized egg of the same species, it seems reasonable to expect that such whole-genome transfers won't be reprogramming arbitrary cells any time in the foreseeable future.
The other things I've been meaning to blog about are stories I ran across earlier this month, also relating to Dr. Venter's efforts to pioneer research on (and patents for) genomic manipulation. For instance, earlier this month Venter's group filed a patent on an "artificial organism" (patent application is here; coverage is here and here). Although the bacterium (derived from another cousin of the two mentioned above, called M. genitalium) is called an artificial organism (dubbed M. laboratorium), I think that gives Venter's group too much credit. Their artificial organism is really just a hobbled version of its parent species, where they removed many of the original genes that were not, apparently, always necessary for a bacterium's survival. From the way the science journalism reads though, you get the impression that Venter et al. have created a bacterium from scratch. I don't think we have either the technology or the scientific understanding of how life works to be able to do that yet, nor do I expect to see it for a long time. But, the idea of engineering bacteria to exhibit different traits (maybe useful traits, such as being able to metabolize some of the crap modern civilizations produce) is already a reality and I'm sure we'll see more work along these lines.
Finally, Venter gave a TED talk in 2005 about his trip to sample the DNA of the ocean at several spots around the world. This talk is actually more about the science (or more pointedly, about how little we know about the diversity of life, as expressed through genes) and less about his commercial interests. It appears that some of the research results from this trip have already appeared on PLoS Biology.
I think many people love to hate Venter, but you do have to give him credit for having enormous ambition, and for, in part, spurring the genomics revolution currently gripping microbiology. Perhaps like many scientists, I'm suspicious of his commercial interests and find the idea of patenting anything about a living organism to be a little absurd, but I also think we're fast approaching the day when we putting bacteria to work doing things that we currently do via complex (and often dirty) industrial processes will be an everyday thing.
posted June 28, 2007 04:13 PM in Things that go squish | permalink | Comments (1)
March 25, 2007
The kaleidoscope in our eyes
Long-time readers of this blog will remember that last summer I received a deluge of email from people taking the "reverse" colorblind test on my webpage. This happened because someone dugg the test, and a Dutch magazine featured it in their 'Net News' section. For those of you who haven't been wasting your time on this blog for quite that long, here's a brief history of the test:
In April of 2001, a close friend of mine, who is red-green colorblind, and I were discussing the differences in our subjective visual experiences. We realized that, in some situations, he could perceive subtle variations in luminosity that I could not. This got us thinking about whether we could design a "reverse" colorblindness test - one that he could pass because he is color blind, and one that I would fail because I am not. Our idea was that we could distract non-colorblind people with bright colors to keep them from noticing "hidden" information in subtle but systematic variations in luminosity.
Color blind is the name we give to people who are only dichromatic, rather than the trichromatic experience that 'normal' people have. This difference is most commonly caused by a genetic mutation that prevents the colorblind retina from producing more than two kinds of photosensitive pigment. As it turns out, most mammals are dichromatic, in roughly the same way that colorblind people are - that is, they have a short-wave pigment (around 400 nm) and a medium-wave pigment (around 500 nm), giving them one channel of color contrast. Humans, and some of our closest primate cousins, are unusual for being trichromatic. So, how did our ancestors shift from being di- to tri-chromatic? For many years, scientists have believed that the gene responsible for our sensitivity in the green part of the spectrum (530 nm) was accidentally duplicated and then diverged slightly, producing a second gene yielding sensitivity to slightly longer wavelengths (560 nm; this is the red-part of the spectrum. Amazingly, the red-pigment differs from the green by only three amino acids, which is somewhere between 3 and 6 mutations).
But, there's a problem with this theory. There's no reason a priori to expect that a mammal with dichromatic vision, who suddenly acquired sensitivity to a third kind of color, would be able to process this information to perceive that color as distinct from the other two. Rather, it might be the case that the animal just perceives this new range of color as being one of the existing color sensations, so, in the case of picking up a red-sensitive pigment, the animal might perceive reds as greens.
As it turns out, though, the mammalian retina and brain are extremely flexible, and in an experiment recently reported in Science, Jeremy Nathans, a neuroscientist at Johns Hopkins, and his colleagues show that a mouse (normally dichromatic, with one pigment being slightly sensitive to ultraviolet, and one being very close to our medium-wave, or green sensitivity) engineered to have the gene for human-style long-wave or red-color sensitivity can in fact perceive red as a distinct color from green. That is, the normally dichromatic retina and brain of the mouse have all the functionality necessary to behave in a trichromatic way. (The always-fascinating-to-read Carl Zimmer, and Nature News have their own takes on this story.)
So, given that a dichromatic retina and brain can perceive three colors if given a third pigment, and a trichromatic retina and brain fail gracefully if one pigment is removed, what is all that extra stuff (in particular, midget cells whose role is apparently to distinguish red and green) in the trichromatic retina and brain for? Presumably, enhanced dichromatic vision is not quite as good as natural trichromatic vision, and those extra neural circuits optimize something. Too bad these transgenic mice can't tell us about the new kaleidoscope in their eyes.
But, not all animals are dichromatic. Birds, reptiles and teleost fish are, in fact, tetrachromatic. Thus, after mammals branched off from these other species millions of years ago, they lost two of these pigments (or, opsins), perhaps during their nocturnal phase, where color vision is less functional. This variation suggests that, indeed, the reverse colorblind test is based on a reasonable hypothesis - trichromatic vision is not as sensitive to variation in luminosity as dichromatic vision is. But why might a deficient trichromatic system (retina + brain) would be more sensitive to luminal variation than a non-deficient one? Since a souped-up dichromatic system - the mouse experiment above - has most of the functionality of a true trichromatic system, perhaps it's not all that surprising that a deficient trichromatic system has most of the functionality of a true dichromatic system.
A general explanation for both phenomena would be that the learning algorithms of the brain and retina organize to extract the maximal amount of information from the light coming into the eye. If this happens to be from two kinds of color contrast, it optimizes toward taking more information from luminal variation. It seems like a small detail to show scientifically that a deficient trichromatic system is more sensitive to luminal variation than a true trichromatic system, but this would be an important step to understanding the learning algorithm that the brain uses to organize itself, developmentally, in response to visual stimulation. Is this information maximization principle the basis of how the brain is able to adapt to such different kinds of inputs?
G. H. Jacobs, G. A. Williams, H. Cahill and J. Nathans, "Emergence of Novel Color Vision in Mice Engineered to Express a Human Cone Photopigment", Science 315 1723 - 1725 (2007).
P. W. Lucas, et al, "Evolution and Function of Routine Trichromatic Vision in Primates", Evolution 57 (11), 2636 - 2643 (2003).
posted March 25, 2007 10:51 AM in Evolution | permalink | Comments (3)
October 01, 2006
Visualizing biology
Aftering seeing it blogged on Cosmic Variance and Shtetl-Optimzed, I wasn't surprised when my friend Josh Adelman wrote to share it, too, with "it" being this wonderful bit of bio-visualization:
A brief popular explanation of the video, which gives substantial background on Harvard's sponsorship of XVIVO, the company that did the work, is here. The video above is apparently a short version of a longer one that will be used in Harvard's undergraduate education; the short version will play at this year's Siggraph 2006 Electronic Theater.
Anyway, what prompted me to blog about this video is that, being a biophysicist, Josh added some valuable additional insight into what's being shown here, and the new(-ish) trend of trying to popularize this stuff through these beautiful animations.
For instance, that determined looking "walker" in the video is actually a kinesin molecule walking along a microtubule, which was originally worked out by the Vale Lab at UCSF, which have their own (more technical) animation of how the walker actually works. Truly, an amazingly little protein.
Another of the more visually stunning bits of the film is the self-assembling behavior of the microtubules themselves. This work was done by the Nogales Lab at Berkeley, and they too have some cool animations that explain how microtubules dynamically assemble and disassemble.
DNA replication hardly makes an appearance in the video above, but the Walter & Eliza Hall Institute produced several visually stunning shorts that show how this process works (the sound-effects are cheesy, but it's clear the budget was well spent on other things).
posted October 1, 2006 03:43 PM in Scientifically Speaking | permalink | Comments (0)
August 30, 2006
Biological complexity: not what you think
I've long been skeptical of the idea that life forms can be linearly ordered in terms of complexity, with mammals (esp. humans) at the top and single-celled organisms at the bottom. Genomic research in the past decade has shown humans to be significantly less complex than we'd initially imagined, having only about 30,000 genes. Now, along comes the recently sequenced genome of the heat-loving bug T. thermophila, which inhabits places too hot for most other forms of life, showing that a mere single-celled organism has roughly 27,000 genes! What are all these genes for? For rapidly adapting to different environments - if a new carbon source appears in its environment, T. thermophila can rapidly shift its metabolic network to consume and process it. That is, T. thermophila seems to have optimized its adaptability via accumulating, and carrying around, a lot of extra genes. This suggests that it tends to inhabit highly variable environments [waves hands], where having those extra genes is ultimately quite useful for its survival. Another fascinating trick it's learned is that it's reproductive behavior shows evidence of a kind of genetic immune system, in which foreign (viral) DNA is excised before sexual reproduction.
From the abstract:
... the gene set is robust, with more than 27,000 predicted protein-coding genes, 15,000 of which have strong matches to genes in other organisms. The functional diversity encoded by these genes is substantial and reflects the complexity of processes required for a free-living, predatory, single-celled organism. This is highlighted by the abundance of lineage-specific duplications of genes with predicted roles in sensing and responding to environmental conditions (e.g., kinases), using diverse resources (e.g., proteases and transporters), and generating structural complexity (e.g., kinesins and dyneins). In contrast to the other lineages of alveolates (apicomplexans and dinoflagellates), no compelling evidence could be found for plastid-derived genes in the genome. [...] The combination of the genome sequence, the functional diversity encoded therein, and the presence of some pathways missing from other model organisms makes T. thermophila an ideal model for functional genomic studies to address biological, biomedical, and biotechnological questions of fundamental importance.
J. A. Eisen et al. Macronuclear Genome Sequence of the Ciliate Tetrahymena thermophila, a Model Eukaryote. PLOS Biology, 4(9), e286 (2006). [pdf]
Update Sept. 7: Jonathan Eisen, lead author on the paper, stops by to comment about the misleading name of T. thermophilia. He has his own blog over at Tree of Life, where he talks a little more about the significance of the work. Welcome Jonathan, and congrats on the great work!
posted August 30, 2006 02:20 PM in Evolution | permalink | Comments (3)