|
Statistical Analysis of
the LiveJournal Network
During the summer of 2003, while searching for a
project at the Santa
Fe Institute Complex Systems Summer School, I began casting
about for large social networks to analyze. Knowing that most
of the important work on understanding the common statistical
structural properties of social networks had been done, but that
little had been done on enormous networks, I specifically began
looking for them.
Brad Fitzgerald, Pete Krawczyk, and Evan Martine
at LiveJournal very kindly offered me an anonymized snapshot of
the LJ network from that summer. Over the next few months, I ran
the statistical methods described in Mark Newmans "Structure
and funtion of networks" review article. My results follow.
| total number of people (N) |
798,017 |
| total number of relationships (E) |
6,410,380 |
| average number of contacts (mean degree) |
16.0654 /- 34.8178 |
| highest number of contacts (max degree) |
9832 contacts |
| cluster coefficient (1) |
0.218334 |
| cluster coefficient (2) |
0.308404 |
| average hand-shake separation (harmonic mean) |
5.2113 |
| largest hand-shake separation (diameter) |
15 |
To make the network analysis more simple, all relationships
were assumed to be reflexive (i.e., symmetric - the graph was
converted into an undirected version of the original data). Briefly,
these results line up nicely with the standard ones for social
networks. Specifically, we see that there is an incredibly high
degree of clustering (a.k.a. network transitivity) representing
the presence of many more triangles of friends than one would
expect in an Erdos-Renyi random graph. We also see a relatively
small diameter for the size of the network (15) and a mean separation
degree which lines up with the seminal Stanley Milgram study of
the 1960s and the more recent study by Duncan Watts. Of particular
note however, and somewhat surprising for a purely social network,
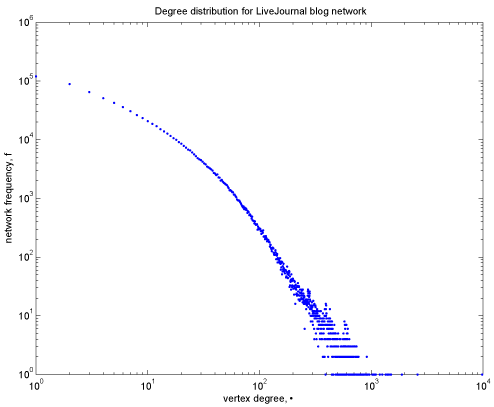
the degree distribution bears a strong resemblance to a power
law for the higher degrees. This result is somewhat surprising,
as one would expect in a physical social network that relationships
would require some degree of maintenence and thus one would not
see individuals with nearly 10,000 relationships; however, in
electronic social networks, such maintenance is not required as
once established a friendship can be forever.
Moving forward on this work, I'm collaborating with
Mark Newman to improve his community structure inference algorithm
so that it scales up to enormous networks like this. One interesting
idea one could explore with the LJ data is to see how well individual
community declarations (LiveJournal supports special nodes called
'communities' which members may join) reflect the actual community
structure discovered via the betweenness-centrality (or modularity)
metric. It seems likely that the interests in a person's local
social network is representative of one's interests as well.
|
|

