6:Parallel Lines

DEFINITION: Parallel lines are infinite lines in the same plane that do not intersect.

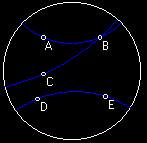
In the figure above, Hyperbolic Line BA and Hyperbolic Line BC are both infinite lines in the same plane. They intersect at point B and , therefore, they are NOT parallel Hyperbolic lines. Hyperbolic line DE and Hyperbolic Line BA are also both infinite lines in the same plane, and since they do not intersect, DE is parallel to BA. Likewise, Hyperbolic Line DE is also parallel to Hyperbolic Line BC. Now this is an odd thing since we know that in Euclidean geometry:

If two lines are parallel to a third line, then the two lines are parallel to each other. This is a theorem in Euclidean geometry, yet in hyperbolic geometry it is proved false by the above counter example (Both BA and BC are parallel to DE, yet BA is not parallel to BC). However, you may not be convinced that BA and DE are parallel. In order to help convince you, I would like to first focus on the fact that each of the lines shown above is Infinite. The lines do not look infinite. We generally think of infinite lines as lines that go on forever, but actually, infinite lines are lines that do not have an end. "Going on forever", and "not having an end" are not the same thing. Remember that in this model of Hyperbolic Geometry, objects get smaller as they get closer and closer to the Boundary Circle, and that the distance from any point within the Boundary Circle to the edge of the Boundary Circle is Infinite. Even if a hyperbolic line segment is 100 million, miles long, then it still would not reach the Boundary Circle, and either end of the line segment can be extended.

A Hyperbolic Line is not the same thing as a Euclidean Line (for example, Hyperbolic Lines curve). They do, however, share many analogous properties. The following is a list of some of these properties:

In Euclidean geometry, there is one and only one shortest path between any two points. We call this "shortest path" the "straight" path, and this path lies along the line segment joining the two points. Exactly the same statement is true in hyperbolic geometry with Hyperbolic Points and Hyperbolic lines.
In Euclidean geometry, two points determine a unique line. In-other-words, given any two points, there exists a line that passes through those two points. Additionally, there does not exist any other line that will pass through both of those two points. Exactly the same statement is true in Hyperbolic Geometry.
In Euclidean geometry, light, in a vacuum, travels along a Euclidean Line. Likewise, in hyperbolic geometry, light, in a vacuum, travels along a hyperbolic line.

Is spite of these similarities Hyperbolic lines have many different properties from Euclidean Lines. For example, the following Euclidean geometry theorems are FALSE in hyperbolic geometry:

In Euclidean geometry, if two lines are parallel to a third line, then the two lines are parallel to each other.
In Euclidean geometry, if two lines are parallel then, the two lines are equi-distant.
In Euclidean geometry, lines that do not have an end (infinite lines), also do not have a boundary (a point that they are headed toward, yet never reach).

NonEuclid Home
Next Topic - 7: Axioms and Theorems