« Hanging out with rock scientists | Main | SFI is hiring again »

October 15, 2008

Power laws in the mist

Flipping through last week's Science yesterday, I was pleasantly surprised to see another entry [1] in the ongoing effort to construct a map of all protein interactions in the model organism yeast (S. cerevisiae). The idea here is that since sequencing DNA is now relatively easy, and we have a pretty good idea of which genes code for proteins, it would be useful to know which of these proteins actually interact with each other. As it's often said, DNA gives us a "parts list" of an organism, but doesn't tell us much about how those parts work together to make life happen [2].

The construction of this "interactome" is a tricky task, requiring us to first build all the proteins, and then to test each pair for whether they interact. The first step is easy with modern methods. The second step, however, is hard: it requires us to test 100-1000 million possible interactions, which would take even a very diligent graduate lab many lifetimes to finish. Instead of that kind of brute-force approach, scientists rely on clever molecular techniques to test for many interactions at once. There have been several high profile efforts along these lines [3], and, many would argue, a lot of real progress.

With an interactome map in hand, the hope is that we can ask biologically meaningful questions about the patterns of interactions, i.e., we can do network analysis on it, and shed light on fundamental questions about how cells work as a whole. We know now that there are some rather serious problems with molecular methods used to infer the interaction network, and these cause more cautious scientists to wonder how much real biology our current maps actually capture [4]. On the other hand, each new interactome is probably better than the last one because molecular techniques do improve, and we know more about how to deal with their problems.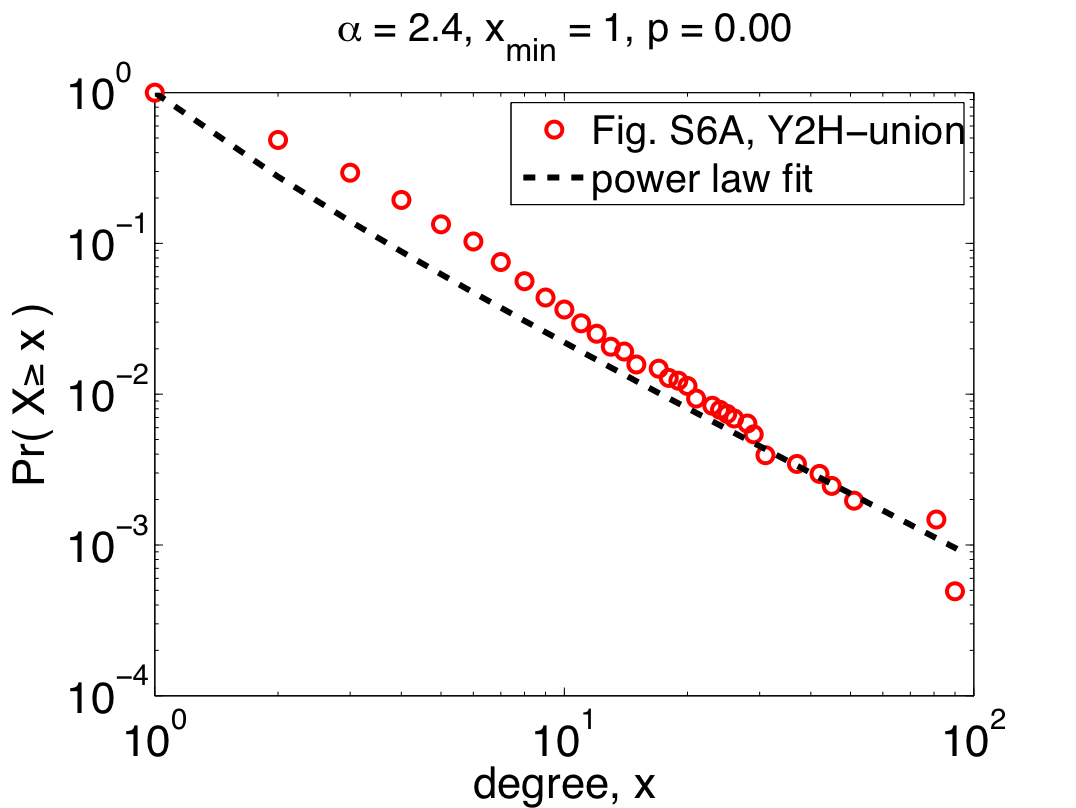

All this stuff aside, even if we take the inferred data at face value, there continue to be problems with its interpretation. For instance, a popular question to ask of interactome data is whether the degree distribution of the network is "scale free." If it does follow a power-law distribution, then this is viewed as being interesting, and perhaps support for some of the several theories about the large-scale organization of such networks.

Answering this kind of question requires care, however, and long-time readers will already know where I'm going with this train of thought. In the text, Yu et al. say

As found previously for other macromolecular networks, the "connectivity" or degree distribution of all three data sets is best approximated by a power-law."

To the right is their data [5] for the Y2H-union data set (one of the three claimed to follow power laws), replotted as a complementary cumulative distribution function (CDF) [6], which cleans up some of the visual noise in the original plot. On top of their data, I've plotted the power-law distribution they quote in their paper (alpha=2.4), which shows just how horrible their fit actually is. We can quantitatively measure how good the fit is by calculating a p-value for the fit (p=0.00 +/- 0.03) [7], which shows that the data definitely do not follow the claimed power law. So much for being scale free? Maybe.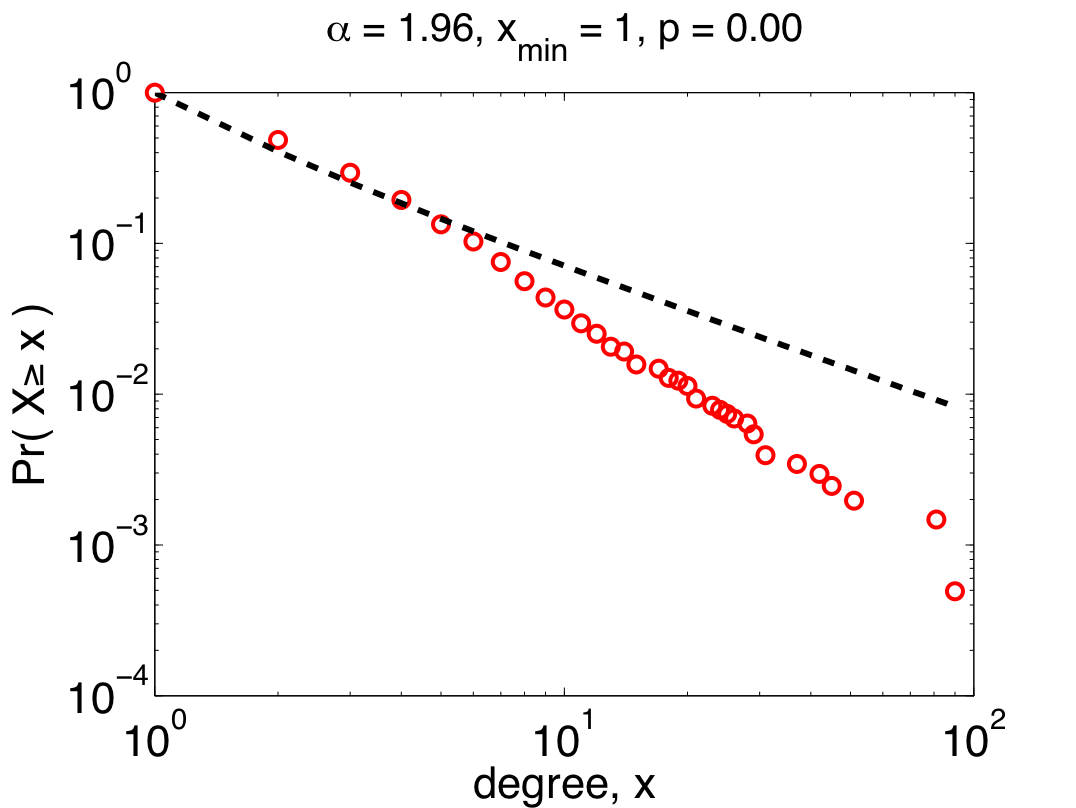

The authors' first mistake was to use linear regression to fit a power law to their data, which can dramatically overweight the large but rare events and, more often than not, finds power-law behavior when none really exists. A better method for choosing alpha is maximum likelihood. If we do this naively, i.e., assuming that all of our data are drawn from a power law, we get the plot on the left.

The fit here is better for more of the data (which is concentrated among the small values of x), but pretty terrible for larger values. And the p-value is still too small for this power-law to be a plausible model of the data. So, the "scale free" claim still seems problematic.

But, we can be more sophisticated by assuming that only the larger values in the data are actually distributed like a power law. This nuance is reasonable since being "scale free" shouldn't depend on what happens for small values of x. Using appropriate tools [8] to choose the place where the power-law behavior starts, we get the power law on the right. Now, we have a more nuanced picture: the 200-odd largest values in the data set (about 10% of the proteins) really are plausibly distributed (p=0.95 +\- 0.03) like a power law, while small values are distributed in some other, non-power-law, way.

So, although the patterns of interactions for large-degree proteins in the Y2H-union data do seem to follow a power law, it is not the power law that the authors claim it is. And, since the truly plausible power-law behavior only holds for top 10% of the proteins, it means there must be a lot of non-scale-free structure in the network. This structure may have evolutionary or functional significance, since it's behavior is qualitatively different from the large-degree proteins. Unfortunately, the authors missed the opportunity to identify or discuss this because they were sloppy in their analysis. The moral here is that doing the statistics right can shed new light on the interactome's structure, and can actually generate new questions for future work.

So far, I've only shown the re-analysis of one of their three data sets, but repeating the same steps with their other two data sets (Combined-AP/MS and LC-multiple) yields similarly worrying results: the Combined-AP/MS data cannot be considered power-law distributed by any stretch of the imagination, and the LC-multiple data are a marginal case. These conclusions certainly mean something about the structure of the different interactomes, but the authors again miss an opportunity to discuss it. The table below summarizes the re-analysis results for the three data sets; the power laws quoted by Yu et al. are given under the heading "regression", while the correct fits are under the second heading:

Notably, the quoted power laws are completely incompatible with the maximum likelihood ones, illustrating that even when there is power-law behavior to be found (e.g., in the Y2H-union data) regression misleads us. Worse, when there is no power-law behavior to be found, regression can give us spuriously high confidence (e.g., the R^2 value for the Combined-AP/MS data). Since pictures are also fun, here are the remaining two plots of the maximum likelihood power laws, showing pretty clearly why the Combined-AP/MS can be rejected as a power law.

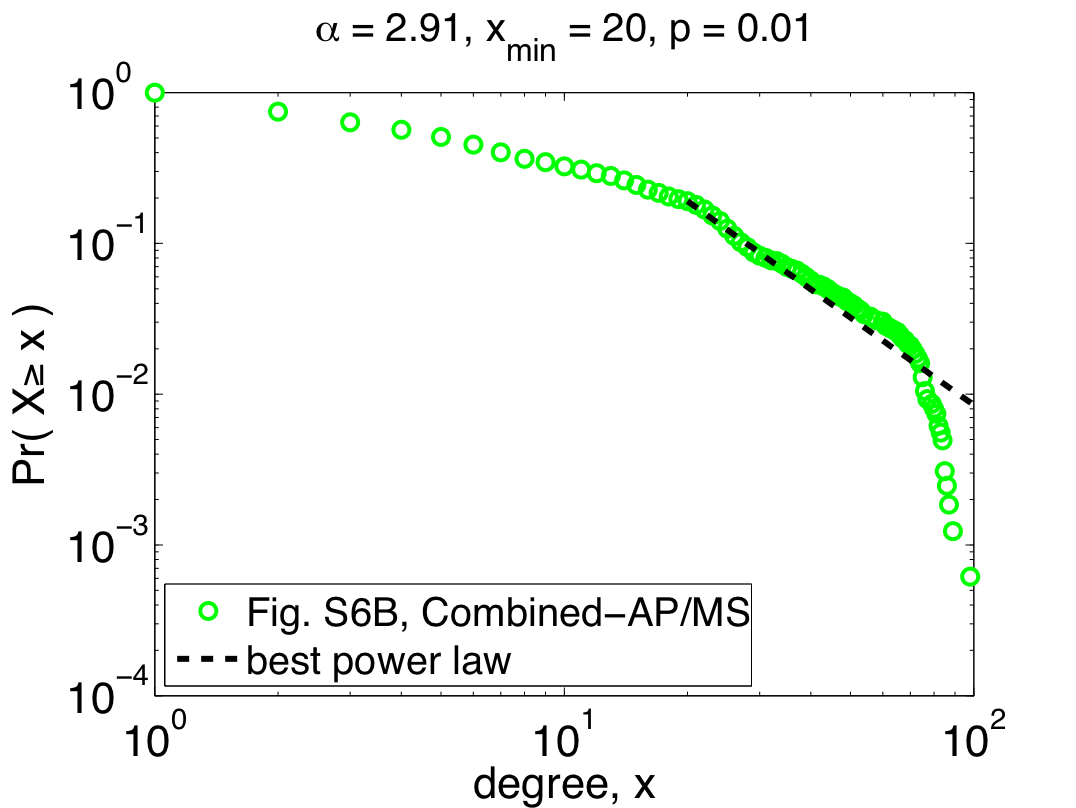
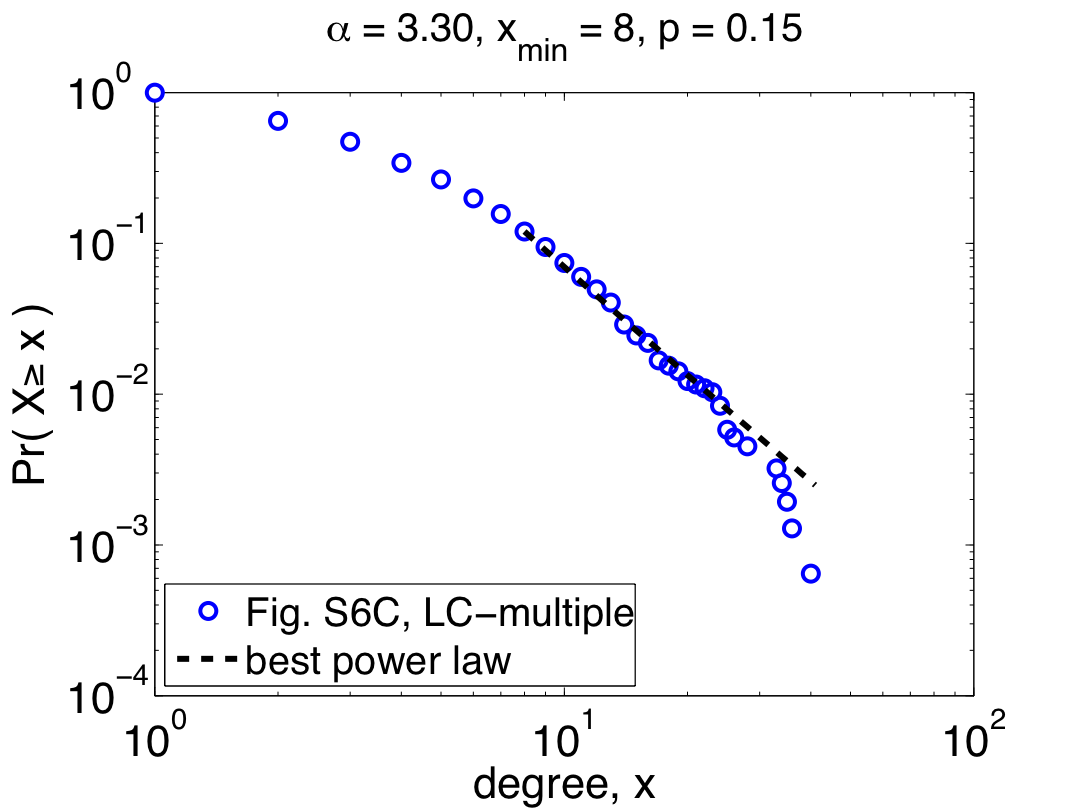
But, not content to merely claim power-law behavior, the authors go on to claim that the power law was the best model [9]. Digging around in the appendices, you find out that they compared their power law with one alternative, a power law with an exponential cutoff (also fitted using regression). Unfortunately, regressions are also the wrong tool for this kind of question, and so this claim is also likely to be wrong [10]. In fact, adding an exponential cutoff is almost always a better model of data than a regular power law. If you felt like wearing your cynical hat today, you might conclude that the authors had some non-scientific motivation to conclude that these networks were "scale free".

There are many aspects of the Yu et al. study that seem entirely reasonable, and majority of the paper is about the experimental work to actually construct their version of the yeast interactome. In this sense, the paper does push the field forward in a meaningful way, and it's mildly unfair of me to critique only the power-law analysis in the paper -- a small part of a very large project.

On the other hand, the goal of constructing interactomes is to ultimately understand what mechanisms create the observed patterns of interactions, and if we're ever to build scientific theories here, then we sure had better get the details right. Anyway, I'm hopeful that the community will eventually stop doing ridiculous things with power-law distributed data, but until reviewers start demanding it, I think we'll see a lot more sloppy science and missed opportunities, and our scientific understanding of the interactome's structure and its implications for cellular function will suffer.

Update 17 October 2008: Nathan Eagle suggested that a bit more detail on why maximum likelihood is preferable to regression in this case would be useful. So, here it is:

Whenever you're fitting a model to data, there are some properties you want your fitting procedure to have in order to trust it's results. The most important of these is consistency. Consider a game in which I play the role of Nature and generate some power-law distributed data for you. You then play the role of Scientist and try to figure out which power law I used to generate the data (i.e., what values of alpha and xmin I chose before I generated the data). A consistent procedure is one whose answers get closer to the truth the more data I show you.

Maximum likelihood estimators (MLEs) are guaranteed to be consistent (they also have normally-distributed errors, which lets you quote a "standard error" for how precise your answer is), which means you can trust them not to mislead you. In fact, regression techniques like least squares are MLEs for a situation where two measurable properties (e.g., pressure and volume) are related, modulo normal measurement errors. But, these assumptions fail if the data is instead a distribution, which means regression methods are not consistent for detecting power-law distributions. In other words, using regression to detect a power-law distribution applies the wrong model to the problem, and it should be no surprise that it produces wildly inaccurate guesses about power-law behavior. More problematically, though, it doesn't give any warning that it's misbehaving, which can lead to confident claims of power-law distributions when none actually exist (as in the Combined-AP/MS case above). If you're still thirsty for more details, you can find them in Appendix A of [8] below.

Update 6 January 2009: There's now a version of these comments on the arxiv.

-----

[1] Yu et al., "High Quality Binary Protein Interaction Map of the Yeast Interactome Network." Science 322, 104 (2008).

[2] Although scientists in this area often talk about how important the interactome is for understanding how life works, it's only part of the puzzle. Arguably, a much more important problem is understanding how genes interact and regulate each other.

[3] For yeast, these are basically Fromont-Racine, Rain and Legrain, Nature Genetics 16, 277 (1997), Uetz et al., Nature 402, 623 (2000), and Ito et al., PNAS 98, 4569 (2001).

[4] For instance, worryingly high false-positive rates, ridiculously high false-negative rates (some of these are driven by the particular kind of molecular trick used, which can miss whole classes of proteins, e.g., nucleus-bound ones) and a large amount of irreproducibility by alternative techniques or other groups. This last point leads me to believe that all of the results so far should not yet be trusted. Interested readers could refer to Bader, Chaudhuri, Rothberg and Chant, "Gaining confidence in high-throughput protein interaction networks." Nature Biotechnology, 22 78 (2004).

[5] Admittedly, it's not exactly their data, but rather a very close approximation to it, derived from Fig. S6A in their supporting online material using DataThief and a lot of patience.

[6] The complementary CDF is defined as Pr( X >= x ). If the data are distributed according to a power law, then this function will be straight on log-log axes. The reverse, however, is not true. That is, being straight on log-log axes is not a sufficient condition for being power-law distributed. There are many kinds of data that look straight on log-log axes but which are not power-law distributed.

[7] The conventional use of p-values is to determine whether two things are "significantly different" from each other. If p<0.1, then the conclusion is that they are different. Here, we're testing the reverse: if p>0.1, then we conclude that the two things are plausibly the same.

[8] Clauset, Shalizi and Newman, "Power-law distributions in empirical data." arXiv:0706.1062 (2007).
Implementations of these methods are available for free online.

[9] Actually, the authors say "best approximated by", which is a disingenuous hedge. What does it mean to "approximate" here, and how bad must the approximation be to be considered unreasonable? If the goal is poetry, then maybe approximations like the one they use are okay, but if the goal is science, we should strive for more precise and more meaningful statements.

[10] If they'd wanted to do it right, then they would have used standard, trustworthy tools for comparing their two models, such as a likelihood ratio test.

[11] A colleague of mine asked me why I didn't write this up as an official "Comment" for Science. My response was basically that I didn't think it would make a bit of difference if I did, and it's probably more useful to do it informally here, anyway. My intention is not to trash the Yu et al. paper, which as I mentioned above has a lot of genuinely good bits in it, but rather to point out that the common practices (i.e., regressions) for analyzing power-law distributions in empirical data are terrible, and that better, more reliable methods both exist and are easy to use. Plus, I haven't blogged in a while, and grumping about power laws is as much a favorite past time of mine as publishing bad power laws apparently is for some people.

posted October 15, 2008 03:18 PM in Scientifically Speaking | permalink

Comments

Posted by: DanF at October 16, 2008 08:00 PM

Posted by: Mason at October 28, 2008 03:57 PM